Nombre dérivé en a	f fonction définie sur un intervalle I et a un nombre de I
Le coefficient directeur de la tangente T à la courbe C représentative de f au point de coordonnées (a, f(a)) est appelé nombre dérivé de f en a et est noté f’(a). Il est égal à la limite si elle existe du taux d’accroissement de la fonction entre a et a + h lorsque h tend vers 0 :

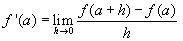
Equation réduite de la tangente

Au point d’abscisse a, l’équation réduite de la tangente à la courbe C représentant f est :
y = f’(a)(x-a) + f(a)

Fonction dérivée
Soit une fonction f qui admet un nombre dérivé f’(x) en tout x d’un intervalle I.
La fonction f’ qui, à tout x de I, fait correspondre le nombre f’(x) est appelé fonction dérivée de f sur I.
f est alors dérivable sur I