Méthodes de correction - Partie 6
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
A l'issue d'un QCU de mathématiques portant sur les probabilités, le correcteur constate que les notes obtenues par les étudiants de la promotion se répartissent approximativement selon une loi normale de paramètres
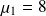et
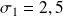. On note
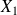la variable aléatoire prenant comme valeur la note d'une copie tirée au sort parmi toutes les copies. On considère donc que
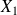suit la loi normale
.
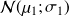Par ailleurs, on note T une variable aléatoire suivant une loi normale centrée réduite
.
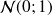Pour les calculs relatifs à la loi normale centrée réduite, on utilisera la table téléchargeable en cliquant ici. Lorsque les calculs impliqueront une valeur comprise entre deux valeurs tabulées, on utilisera la valeur tabulée la plus proche.
Après mûre réflexion, le correcteur ne souhaite plus intervenir sur les notes en modifiant la moyenne
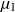des notes obtenues mais uniquement l'écart-type de sorte que la proportion de notes supérieures ou égales à 15 soit également de 5%. Avec cette méthode, les notes modifiées seront représentées par une variable aléatoire
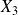suivant une loi normale de moyenne
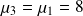et d'écart-type
.
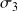Quelle doit être, à 0,1 près, la valeur de
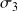? (Penser à faire défiler l'écran vers le bas si la résolution d'écran ou la taille de la fenêtre ne permettent pas l'affichage de toutes les propositions...)
En appliquant le changement de variable
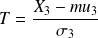à l'information fournie, on a :
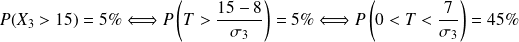
Avec une lecture inverse de la table de la loi normale centrée réduite, on en déduit alors la valeur de
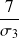, d'où on tire celle de
.
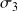