La bonne étoile - Partie 4
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
Un étudiant subit un examen de mathématiques portant sur les probabilités, cet examen se présentant sous la forme d'un QCU (Questionnaire à Choix Unique). On considère le cas où l'étudiant n'a pas révisé et décide de ne pas tricher mais plutôt de faire confiance à sa "bonne étoile".
L'étudiant répond donc purement au hasard aux questions posées. A chaque question, il n'y a qu'une seule bonne réponse parmi 4 propositions (principe même du QCU !). L'étudiant ne s'abstient pas et coche systématiquement une seule réponse. Le QCU comporte 10 questions indépendantes.
On note X la variable aléatoire représentant le nombre de bonnes réponses cochées par l'étudiant à l'issue de l'examen.
Que vaut, à 0,0001 près, la probabilité que l'étudiant réponde correctement à exactement 2 questions ? (Penser à faire défiler l'écran vers le bas si la résolution d'écran ou la taille de la fenêtre ne permettent pas l'affichage de toutes les propositions...)
Pour une variable aléatoire
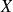suivant une loi binomiale de paramètres
et
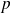, la loi de probabilité est donnée par la formule :
