Révision sur les annales - Partie 1
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
A la veille d'un examen de mathématiques portant sur les probabilités, un étudiant consciencieux s'entraîne en consultant les annales des années précédentes. La forme de l'évaluation sera un questionnaire à choix unique (QCU) et l'étudiant a identifié 4 thèmes notés A, B, C et D pour conduire ses révisions. Il sait que les questions auxquelles il aura à répondre pourront faire appel à plusieurs de ces thèmes à la fois.
Après avoir cherché dans les annales un très grand nombre de questions, l'étudiant est en mesure de dire que :
1 question sur 4 fait appel au thème A
3 questions sur 5 font appel au thème A ou au thème B
3 questions sur 20 font appel à la fois au thème A et au thème B
1 question sur 3 ne fait pas appel au thème C
parmi les questions faisant appel au thème D, 2 sur 3 font appel au thème C
5 questions sur 6 font appel au thème A ou au thème C
On tire une question au hasard parmi les annales compulsées. Quelle est la probabilité, à 0,01 près, qu'elle fasse appel au thème B ? (Penser à faire défiler l'écran vers le bas si la résolution d'écran ou la taille de la fenêtre ne permettent pas l'affichage de toutes les propositions...)
Notant A (respectivement B) l'événement "Tirer une question faisant appel au thème A (respectivement B)", on peut s'appuyer sur la formule :
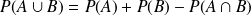
Dans cette formule en effet, seule P(B) est inconnue...





