Sur l’intervalle 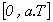, k1 est fermé et la diode D est bloquée.

Dessiner le montage supposé actif (c’est à dire l’ensemble des composants et des conducteurs qui sont alors parcourus par un courant).

En déduire que le circuit actif est un circuit " R L " série, soumis à une tension constante.

On sait que, dans ce cas, l’équation de 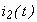est une exponentielle.

On peut trouver l’expression de 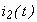en déterminant trois informations :

• la " condition initiale " (déterminée par la non-discontinuité du courant dans une inductance)
• la " valeur finale " (c’est à dire l’asymptote de la courbe) déterminée par le " schéma de régime forcé ".
• la constante de temps déterminée par le " schéma de régime libre "

Avec ces trois informations, on peut :

soit calculer la solution de l’équation différentielle de premier ordre,

soit utiliser directement la solution de celle-ci donnée sous la forme générale :

.

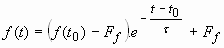Pour plus d’informations, consulter le chapitre 1 " Introduction à l’électronique de puissance " ; Annexe : Rappels sur les circuits R.L et R.C en régime transitoire.

ou sur Internet :

Baselecpro.

Après avoir obtenu l’équation de 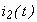, il est facile d’en déduire .
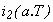