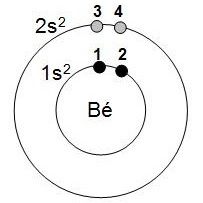
Energies d’ionisations de l’atome de Béryllium :

1- c'est le 4^ème élément :  Z = 4

2- structure électronique : 1s²2s²       (voir classification)

3- groupes selon Slater :   (1s²)(2s²)

4- dessin correspondant

       5- Énergie électronique totale du Béryllium :   
       E_totale(Bé) = Ee₁ + Ee₂ + Ee₃ + Ee₄ = 2 Ee₁ +2 Ee₃

       Deux valeurs de Z à calculer car il y a 2 groupes de Slater    (E₀ = - 13,6 eV)

       Ze₁ = Z₁ = Z₂ = 4 – (1 x 0,3) = 3,7         Ze₃ = Z₃ = Z₄ = 4 – (2 x 0,35) – (1 x 0,85) = 2,45
       Ee₁ = E₁ = E₂ = (3,7² / 1²) x E₀ = - 186,2 eV 
       Ee₃ = E₃ = E₄ = (2,45² / 2²) x (- 13,6 eV) = - 20,4 eV          
       E_totale (Bé) = (2 x - 186,2 ) + (2 x - 20,4) = - 413,2 eV

 

attention, la valeur de E'e3 est différente de Ee3 car le groupe d'électrons est différent (1 e̅ au lieu de 2)

Pour calculer l'énergie électronique totale de l'ion Béryllium (Bé⁺), on reprend les étapes 4 et 5 puis on en déduit I₁ :

4- dessin correspondant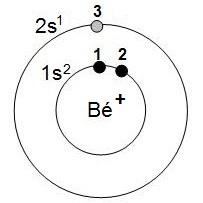

5- Énergie électronique totale de l'ion Béryllium (Bé+) :    Etotale(Bé+) = Ee1 + Ee2 + Ee3 = 2 Ee1 + E'e3 Deux valeurs de Z à calculer car il y a 2 groupes de Slater Z1 = 4 – (1 x 0,3) = 3,7                                       Z'3 = 4 – (2 x 0,85) = 2,3 E1 = (3,72 / 12) x (- 13,6 eV) = - 186,2 eV    E'3 = (2,32 / 22) x (- 13,6 eV) = - 18,0 eV Etotale (Bé+) = (2 x - 186,2 ) + (- 20,4) = - 390,4 eV 6- I1 = Etotale (Bé+) - Etotale (Bé)        soit        I1 = (- 390,4) - (- 413,2) = 22,8 eV

La valeur est éloignée de la valeur expérimentale car la théorie de Slater ne tient pas compte de
la stabilisation qu'apporte l'existence d'une couche complète.
 

4- dessin correspondant

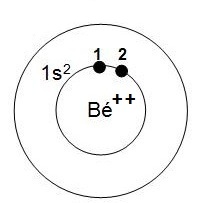
5- Énergie électronique totale de l'ion Béryllium (Bé++) :    Etotale(Bé++) = Ee1 + Ee2 = 2 Ee1 Une seule valeur de Z à calculer car il y a 1 seul groupe de Slater Z1 = 4 – (1 x 0,3) = 3,7 E1 = (3,72 / 12) x  (- 13,6 eV) = - 186,2 eV            Etotale (Bé++) = (2 x - 186,2 ) = - 372,4 eV 6- I2 = Etotale (Bé++) - Etotale (Bé+)        soit        I2 = (- 372,4) - (- 390,4) = 18,0 eV

4- dessin correspondant

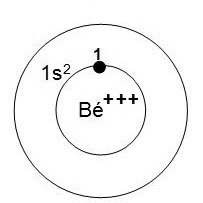
5- Énergie électronique totale de l'ion Béryllium (Bé+++) :    Etotale(Bé+++) = E'e1 Une seule valeur de Z à calculer car il y a 1 seul groupe de Slater Z'1 = 4 car il n'y a qu'un seul électron           E'1 = (42 / 12) x (- 13,6 eV) = - 217,6 eV Etotale (Bé+++) = - 217,6 eV 6- I3 = Etotale (Bé+++) - Etotale (Bé++)        soit        I3 = (- 217,6) - (- 372,4) = 154,8 eV

12- Énergie électronique totale de l'ion Béryllium (Bé⁺⁺⁺⁺) est nulle car il ne possède aucun électron !

E_totale(Bé⁺⁺⁺⁺) = 0

13- I₄ = E_totale (Bé⁺⁺⁺⁺) - E_totale (Bé⁺⁺⁺)        soit        I₄ = 0 - (- 217,6) = 217,6 eV
 

Les valeurs sont proches des valeurs expérimentales, ce qui montre la validité de la théorie de Slater, lorsqu'aucun phénomène ne stabilise une configuration électronique (la majorité des cas). Les électrons de la couche de valence mobilisent quelques dizaines d'eV alors que pour les électrons des couches internes, il faut au moins dix fois plus d'énergie (ils ne pourront être mobilisés dans les liaisons chimiques).

Pensez à vérifier vos acquis et cochez les cases à la première page lorsque vous vous sentez capable de répondre à la requête proposée.