La loi exponentielle
Définition
Soit X une variable aléatoire définie sur (Ω ; P). On dit que X suit une loi exponentielle de paramètre λ > 0 si X admet pour densité la fonction f définie par :
- Pour x < 0, f(x) = 0,
- pour x ≥ 0, f(x) = λe-λx
Voici un exemple de représentation graphique de f :
La fonction de répartition
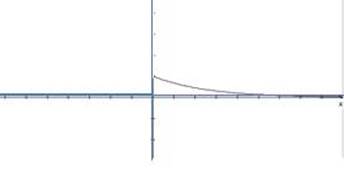
La fonction de répartition de la variable aléatoire X est alors définie par :
Si x < 0, F(x) = 0,
Si x ≥ 0, F(x) = 1-e-λx
Voici un exemple de représentation graphique de F :
Espérance mathématique et variance
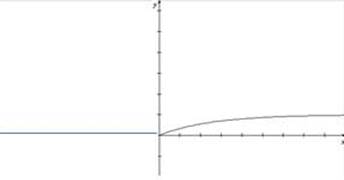
Soit X une variable aléatoire définie sur (Ω ; P), suivant une loi exponentielle de paramètre λ > 0.
Alors nous admettons :
E(X) = 1/λ,
V(X) = 1/λ2
Utilisation pratique
Supposons que l'on modélise le nombre de clients entrant dans un magasin pendant un laps de temps de 1 heure. Si le nombre moyen de clients entrants est égal à λ, alors la variable aléatoire égale au nombre de clients entrant dans le magasin pendant une heure suit une loi de Poisson de paramètre λ (voir le cours variables aléatoires 2 : cas des univers infinis dénombrables).
Si on fixe une origine des temps (par exemple à partir de maintenant, ou de 9 h du matin...), et que l'on appelle variable aléatoire X le temps d'attente avant que le premier client rentre dans le magasin, alors X suit la loi exponentielle de paramètre λ.