Vous pouvez vous passer de ce qui suit et être un utilisateur de la loi Normale.

Beaucoup d'utilisateurs ont une culture des intégrales et des intégrales généralisées inexistante. Cela ne les empêche pas de comprendre les résultats obtenus par ces moyens.

Mais vous pouvez aussi être curieux, surtout qu'il est annoncé un peu de mathématiques et que tout n'est pas formalisé, loin s'en faut !

Ceux qui ne souhaitent pas faire de mathématiques peuvent aller directement au paragraphe "Définition pour tous".

Dans l'exemple, nous avons vu que la probabilité de l'évènement (X=x) est toujours égale à zéro.

On doit donc additionner des zéros et trouver 1 ...car la probabilité de l'univers est égale à 1.

Si l'univers Ω est fini ou infini dénombrable, ce n'est pas possible.

Or, ici, l'univers Ω est  infini et non dénombrable.

Il faut par conséquent "généraliser" le symbole Σ, ce qui se fait par des intégrales.

Dans toute la suite, nous supposerons que Ω est l'ensemble des nombres réels R.

Nous allons donc formaliser tout cela pour arriver à la notion de densité.

I) Soit f une fonction intégrable sur [a ; b], intervalle de R. Si x est un nombre réel de l'intervalle [a ; b], alors f est intégrable sur l'intervalle [a ; x] et si on pose :

1. F est continue sur [a ; b],
2. F est dérivable à gauche en tout point x₀ de ]a ; b] où f admet une limite à gauche (idem à droite) et F'_g(x₀)= f(x₀-).

Dans le cadre de ce cours, retenez que : pour tous les points de [a ; b] où f est continue, F'(x₀)=f(x₀).

II) Soit f une fonction définie sur [a ; +∞[ et intégrable sur tout intervalle [a ; x]. On dit que l'intégrale

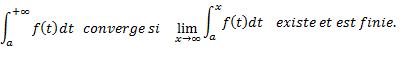
Sinon, on dit que l'intégrale diverge.

On parle alors d'intégrale généralisée.

Les propriétés énoncées au I) restent valables pour les intégrales généralisées, à condition qu'il y ait convergence.