Si l'univers est infini non dénombrable ( pour nous, R), on construit un esapce probabilisé en utilisant les intervalles de R.

On définit donc la distribution d'une variable aléatoire continue à partir de la probabilité des évènements suivants :

• ]-∞ ; a] = (X≤ a),
• [a ; b] = (a ≤ X ≤ b),
• {a} = (X=a)
• ...

Soit X une variable aléatoire définie sur R, l'ensemble des nombres réels. Soit F_X sa fonction de répartition.

On dira que X est une variable aléatoire continue sur R s'il existe une fonction f de R dans R, telle que :

1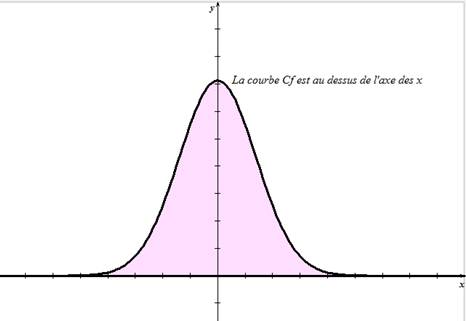
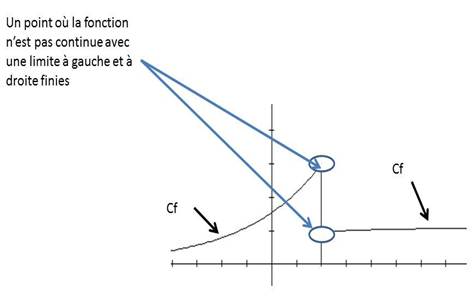
2	f est continue sur R, sauf éventuellement en un nombre fini de points où elle a une limite à droite et à gauche finies.
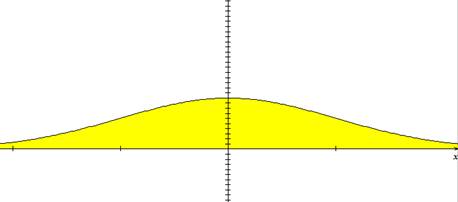
3	L'aire coloriée en jaune est égale à 1.
4
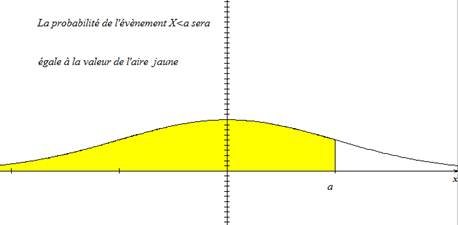