Parmi les utilisations les plus courantes du théorème ou de ses dérivés, on citera la façon d'exprimer la distance entre deux points en coordonnées cartésiennes dans un repère orthonormé.

• Ainsi, si A(xa,ya) et B(xb,yb) sont des points du plan euclidien, la distance les séparant est donnée par :

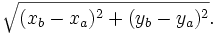
• En effet, si C est le point de coordonnées (xb,ya), le triangle ACB est rectangle en C.

• Les distances CA et CB sont données par CA = |xb - xa| et CB = |yb - ya| et la distance AB représente l'hypoténuse du triangle rectangle ACB.

• Plus généralement, dans un espace euclidien (ou dans un espace affine euclidien) de dimension finie, la distance de 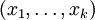à 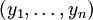s'écrit :

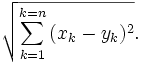
Le théorème de Pythagore se généralise aussi dans des espaces de plus haute dimension.

• Par exemple, si un tétraèdre possède un coin formé d'angle droit (un coin de cube), alors le carré de l'aire de la face opposée au coin est la somme des carrés des aires des trois autres faces.

• Ce théorème est aussi connu sous le nom de théorème de Gua.