A) Conditions initiales

Les variables d'état d'un réseau sont les grandeurs qui ne peuvent pas être discontinues :

Intensité dans une inductance

d.d.p. aux bornes d'un condensateur

Les variables d'état servent à déterminer les conditions initiales, c'est à dire les valeurs de toutes les grandeurs juste après la modification des sources du réseau.

 

B) Équations différentielles

1) Méthode générale de résolution

Étape 1 : mettre sous forme canonique

Étape 2 : déterminer la solution générale y1 (t) de l'équation sans second membre

Étape 3 : rechercher une solution particulière y2 (t) de l'équation sans second membre en se donnant une fonction de même forme que le second membre et en procédant par identification

Étape 4 : écrire la solution y (t) = y1 (t)+ y2 (t)

Étape 5 : calculer les constantes d'intégration en utilisant les conditions initiales

2) Équation du premier ordre

Étape 1 : mettre sous forme canonique

y + t.dy/dt = f (t)

Étape 2 : déterminer la solution générale y1 (t) de l'équation sans second membre y1 (t) = A.exp(-t/t)

Étape 3 : rechercher une solution particulière y2 (t) de l'équation sans second membre en se donnant une fonction de même forme que le second membre et en procédant par identification :

f (t) = K Þ y2 (t) = K

f (t) = polynôme de degré n Þ y2 (t) = autre polynôme de degré n

f (t) = fonction sinus de fréquence f Þ

y2 (t) = fonction sinus de même fréquence

Étape 4 : écrire la solution y (t) = y1 (t)+ y2 (t)

Étape 5 : calculer la constante d'intégration A en utilisant la condition initiale y (to).

3) Équation du second ordre

Étape 1 : mettre sous forme canonique: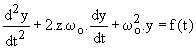

Étape 2 : déterminer la solution générale y1 (t) de l'équation sans second membre

Écrire l'équation caractéristique : .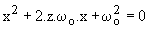

Le déterminant réduit de l'équation est 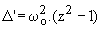. On aura donc 3 cas :

Premier cas : z > 1 ; l'équation caractéristique a alors deux racines réelles négatives: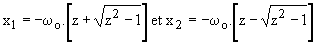

La solution générale est de la forme :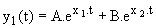

Deuxième cas : z = 1; l'équation caractéristique a alors une racine double -w_o.

Dans ce cas la solution générale est :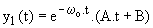

Troisième cas : z < 1; l'équation caractéristique a deux racines complexes conjuguées,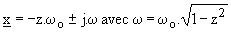

la solution générale est :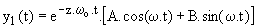

Étape 3 : rechercher une solution particulière y2(t) de l'équation sans second membre

f (t) = K Þ y2 (t) = K/wo²

f (t) = polynôme de degré n Þ y2 (t) = autre polynôme de degré n

f (t) = fonction sinus de fréquence f Þ y2 (t) = fonction sinus de même fréquence

Étape 4 : écrire la solution y (t) = y1 (t)+ y2 (t)

 Étape 5 : calculer les constantes d'intégration A et B en utilisant les conditions initiales y (to) et dy (to)/dt

C) Régime permanent

1) Méthode analytique

Étape 1 : étudier la solution sur l'intervalle [n.T ; (n+1).T] en posant

t' = t-n.T; les constantes d'intégration se calculent de proche en proche à partir de

y(t'=0) = Yo

Étape 2 : Écrire qu'en régime périodique

y (t'=T) = y (t' = 0) et en déduire Yo.

2) Méthode harmonique

Étape 1 : décomposer la f.é.m. source en série de Fourier

Étape 2 :Appliquer le théorème de superposition en gardant dans chaque état un seul harmonique de la f.é.m.