Une enquête auprès d'un groupe de commerçants de vêtements du centre ville de Lyon a permis de relever le nombre de clients entrés dans le magasin pendant une heure ( de neuf heures à dix heures).

Les résultats sont consignés dans le tableau ci-dessous :

Résultats des observations

Nb de clients	0	1	2	3	4	5
Nb de magasins	35	50	40	20	6	3

On cherche à savoir si, au risque 5%, on peut admettre que la population suit une loi de Poisson.

Réponse :

Tout d'abord, H0 s'écrit : la population suit une loi de Poisson.

H1 s'écrit : la population ne suit pas une loi de Poisson.

Il faut ensuite estimer ponctuellement la moyenne et la variance de la population :

La programmation de l'échantillon permet d'estimer ponctuellement la moyenne par 1,49 et la variance 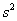par 1,44 .

Remarque1 ; remarque2

Comme pour une loi de Poisson, on a la moyenne 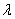égale à la variance , on estime par 1,5.

On obtient alors le tableau suivant : (les valeurs de 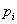sont lues dans la table de Poisson ou bien calculées à l'aide de la formule :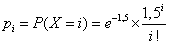

Tableau des effectifs observés et des effectifs calculés

	0	1	2	3	4	5	Total
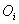	35	50	40	20	6	3	154
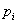	0,2231	0,3347	0,2510	0,1255	0,0471	0,0186	1
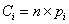	34,35	51,54	38,65	19,33	7,25	2,86	154

La dernière classe a un effectif calculé inférieur à 5, il faut donc regrouper les deux derniers évènements.

Le nouveau tableau obtenu est :

Tableau des effectifs observés et des effectifs calculés

	0	1	2	3	4	Total
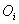	35	50	40	20	9	154
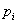	0,2231	0,3347	0,2510	0,1255	0, 0657	1
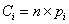	34,35	51,54	38,65	19,33	10,11	154

On a donc :

Après regroupement, il reste 5 évènements et on a estimé un paramètre (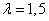). Le nombre de degrés de liberté est donc .

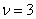Rappel :

Si le risque est de 5%, nous pouvons lire dans la table de la fonction de répartition de la loi du : .

Nous avons donc et nous ne pouvons rejeter au risque 5% l'hypothèse H0.

Pratiquement, cela revient à admettre que la population suit une loi de Poisson.