La loi Normale ou loi de Gauss
Préambule
Si l'on examine les diagrammes en bâtons ou en barres de séries statistiques, il n'est pas rare de rencontrer une forme "classique", ressemblant à une colline, peu ou prou symétrique et plus ou moins haute. Par exemple :
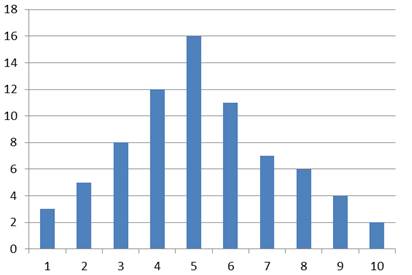
On a cherché alors à trouver un modèle qui corresponde à cette forme dans le cas continu.
Le résultat de ces recherches a donné la loi Normale.
La fonction densité de la loi Normale a pour représentation graphique une courbe en "cloche". Pour coller à la réalité des phénomènes à modéliser, cette courbe en cloche peut se déplacer horizontalement (le sommet de la cloche peut être vers la gauche, le centre, la droite...) et cette cloche peut être plus ou moins "pointue".
Il s'agit maintenant de "mathématiser" ces remarques préalables.
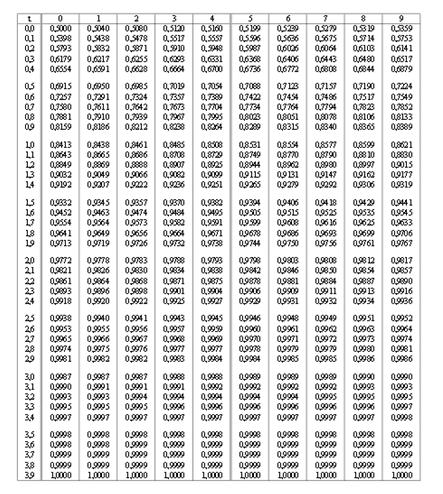
Là encore, il n'est pas indispensable de "faire de la théorie". le lecteur qui veut seulement utiliser la loi Normale pourra se contenter d'utiliser la table correspondante.
Définition
Soit X une variable aléatoire définie sur R. X est une loi Normale (ou de Gauss, ou de Laplace- Gauss) de paramètres μ, nombre réel et σ nombre réel stictement positif si X est une variable aléatoire absolument continue dont une densité est la fonction f définie par :
On dit alors que X suit suit la N(μ ; σ) (lire loi normale - ou de Gauss - de moyenne mu et d'écart-type sigma).
Voici un exemple de représentation graphique de f :
Fonction de répartition
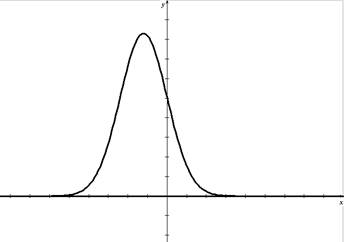
Il est impossible d'expliciter la fonction de répartition F en utilisant les fonctions usuelles. Nous nous contenterons donc d'écrire que F est définie par :
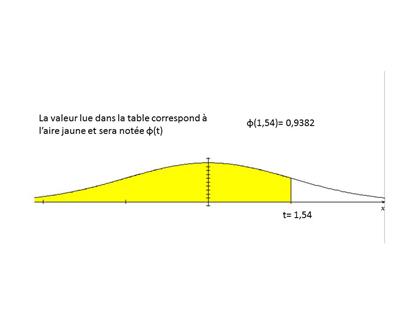
Pour ceux ( et ils sont nombreux !) que cette expression rebute, il suffit de comprendre le schéma ci dessous :
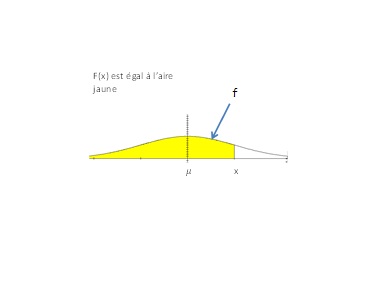
Il suffit de savoir comment calculer l'aire jaune pour connaitre la fonction de répartition.
Notons (et nous en aurons besoin par la suite) que cette courbe admet la droite d'équation (x=μ) comme axe de symétrie.
Il n'est pas dans nos possibilités mathématiques, compte tenu de nos connaissances, de le faire dans le cadre de ce cours. On pourrait construire une table qui répertorie les valeurs de F. Mais il faudrait le faire pour toutes les valeurs de μ et de σ. Il y aurait donc une infinité de tables, ce qui est impossible à faire.
Il va falloir ruser...et passer par la variable centrée réduite (voir plus loin).
Espérance mathématique et variance
Soit X une variable aléatoire suivant une loi N(μ ; σ). On a alors E(x) = μ et V(X) = σ2.
Ces propriétés sont admises.
A posteriori, cela justifie la lecture de N(μ ; σ) sous la forme loi normale - ou de Gauss - de moyenne mu et d'écart-type sigma.
Loi Normale centrée réduite
Soit Y la variable aléatoire suivant la loi N(μ ; σ). Alors, la variable aléatoire X = (Y-μ)/σ est la variable centrée réduite associée à Y.
X suit alors la loi normale centrée réduite N(0 ; 1). Ce changement de variable sera effectué de façon systématique.
Il ne sera pas fait de démonstration. Notons cependant que cette conclusion n'est fondamentale que parce que X suit une loi Normale. Le fait qu'elle soit de moyenne 0 et d'écart-type 1 vient du fait que l'on a centré et réduit...
