Soit X une variable aléatoire définie sur un espace probabilisé (Ω ; P).

Concrètement dans ce qui suit, Ω= R et l'espace est probabilisé en considérant que les évènement sont les intervalles de R.

F est la fonction de répartion de X (rappel : F(x)= P(X≤x)).

On dit que X est une variable aléatoire absolument continue, s'il existe une fonction numérique f, définie sur R, telle que :

On dit alors que f est une densité de X. Par abus de langage, on dira que f est la densité de X, ou la loi de X.

On utilisera aussi les termes "Variable alétoire continue" à la place de "variable aléatoire absolument continue" dans la suite du cours.

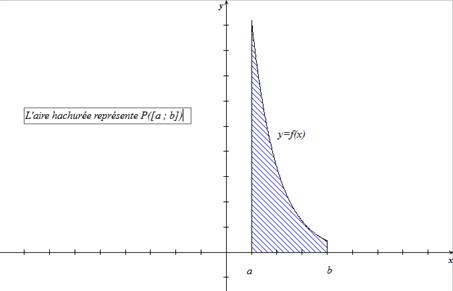
Nous savons que l'interprétation graphique de l'intégrale de la fonction f sur l'intervalle [a ; b] est, une unité étant choisie, l'aire de la surface comprise entre l'axe des x, la courbe représentative de f, les droites verticales d'équation x= a et x=b.

Nous utiliserons cette interprétation pour comprendre comment seront définies les probabilités pour des variables continues dans le cas où on ne fait pas de maths...