Exercice (correction)

Calculer les chaleurs standards de la réaction de synthèse à pression constante et volume constant du tétroxyde de di -hydrogène (N₂H₄) selon la réaction en phase gaz:

N₂ + 2 H₂ ® N₂H₄

Données: D H°_f (N₂H₄) = + 22, 8 Kcal. mol^-1 ; R = 2 cal. mol^-1 .degré^-1

• Détermination directe des chaleurs (énergies) de réaction

- Réactions en phase liquide: Pression constante

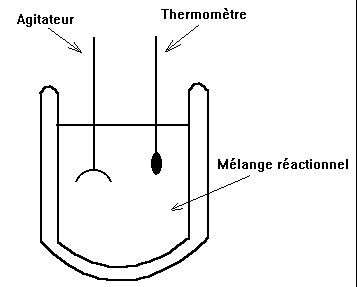
On effectue la réaction dans un calorimètre (calorimètre de Berthelot).

La mesure de l'élévation ou de la diminution de température permet d'accéder à la chaleur de réaction connaissant les Cp des réactifs et produits ainsi que la valeur en eau du calorimètre et de ses accessoires.

- Réaction en phase gaz : Volume constant

On effectue la réaction dans une bombe calorimétrique, elle même plongée dans un calorimètre contenant de l'eau.

Cette méthode concerne essentiellement la détermination des chaleurs de combustion. Le déclenchement de la réaction se fait électriquement (résistance de chauffage ou étincelle).

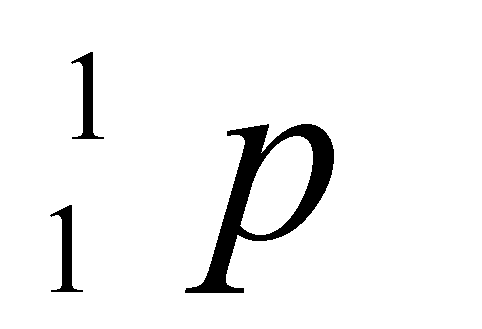
De la même manière que précédemment, la mesure de l'élévation de température permet d'accéder à la chaleur de réaction connaissant les Cv des réactifs et produits ainsi que les caractéristiques du calorimètre.

• Variations des chaleurs de réaction avec la température: Lois de Kirchoff

Démonstration des lois de Kirchhoff

On ne traitera ici que les réactions s'effectuant à pression constante. Pour celles s'effectuant à volume constant, il suffira de remplacer D H par D U et les Cp par les Cv.

Le problème consiste à déterminer le D H d'une réaction pour n'importe quelle température connaissant ce même D H à une température bien déterminée (qui, souvent, est celle de l'état standard mais qui peut être une température quelconque).

On reprend la réaction générale:

aA + bB + cC + ...... ® dD + eE + fF + .......

et on considère le cycle suivant:

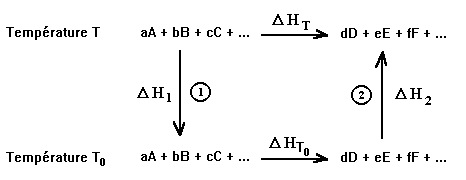
Chemin 1: Les réactifs sont portés de la température T à la température T₀

On a vu précédemment que pour un échange de chaleur à pression constante (cf. 1-4-2-1) on avait:

dQ = Cp . dT soit en intégrant:

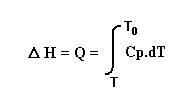
Les Cp étant tous indépendants les uns des autres, on peut tous les mettre sous un signe unique. Mais, comme tous les Cp sont rapportés à une mole de composé, il faut tenir compte des coefficients stœchiométriques de la réaction, soit:

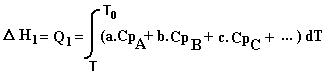
La réaction s'effectue à la température T₀ (D H_T0 )

Chemin 2: Les produits sont portés de la température T₀ à la température T

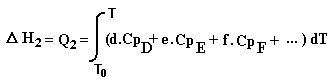
Le cycle permet d'écrire:

D H_T = D H₁ + (D H_T0 ) + D H₂ = (D H_T0 ) + (D H₁ + D H₂ ) soit:

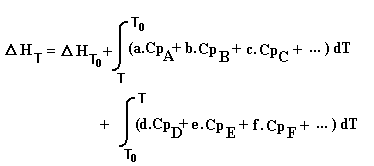
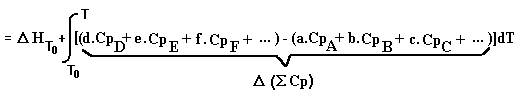
NB Le signe de la première intégrale est changé car on a permuté ses bornes.

• Expression des lois de Kirchhoff

On a donc deux lois de Kirchhoff selon que la réaction s'effectue à pression constante ou à volume constant:

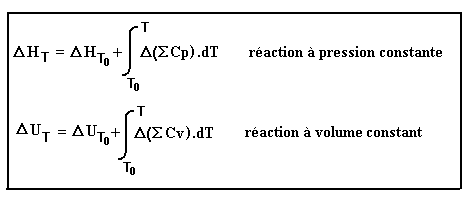
Exercice corrigé II (voir correction)

Calculer, à 450 °C, température à laquelle se fait la synthèse en phase gaz du gaz ammoniac (NH₃) , la chaleur Qp de cette réaction de synthèse selon: N₂ + 3 H₂ ® 2 NH₃

Données: D H°_f (NH₃) = - 10, 98 Kcal. mol^-1 ; Cp (N₂) = 6, 95 cal. mol^-1 .degré^-1 ;

Cp (H₂) = 6, 78 cal. mol^-1 .degré^-1 ; Cp (NH₃) = 8, 89 cal. mol^-1 .degré^-1 .