Déterminer la résistance entre les points A et F. Chaque trait correspond à une résistance de 1 Ω.

 

SOLUTION

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

solution :

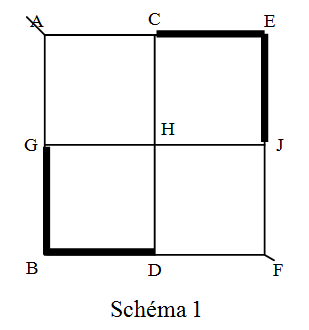
Schéma 1

CE et EJ sont en série : RCJ = 1+1=2 Ω.
GB et BD sont en série : RGD = 1+1=2 Ω.

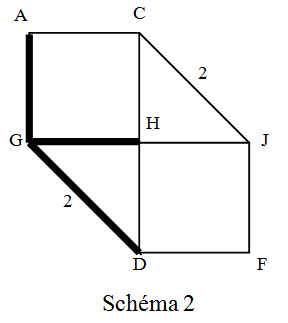
Schéma 2

On remplace l’étoile GH, GA, GD par le triangle AHD
La somme des produits des résistances vaut : 1x1+1x2+2x1=5 Ω
RAH =5/2 Ω            RAD =5/1=5 Ω       RHD =5/1=5 Ω

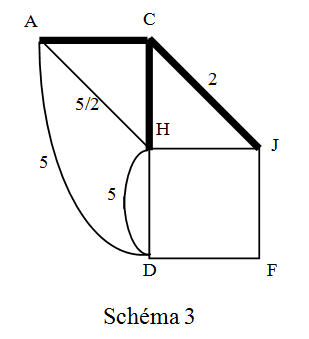
Schéma 3

On remplace l’étoile CA, CH, CJ par le triangle AHJ
La somme des produits des résistances vaut: 1x1+1x2+2x1=5 Ω
RAH =5/2 Ω            RAJ =5/1=5 Ω        RHJ =5/1=5 Ω

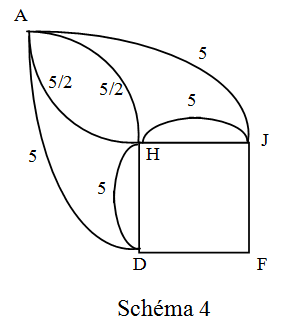
Schéma 4

Entre A et H, 5/2 Ω et 5/2 Ω  en parallèle :RAH=5/4 Ω  
Entre H et J, 5 Ω et 1 Ω en parallèle RHJ=5/6 Ω  
Entre H et D, 5 Ω et 1 Ω en parallèle RHD = 5/6 Ω

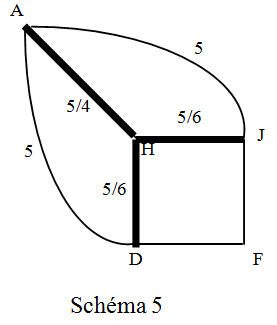
Schéma 5

On remplace l’étoile HA, HJ, HD par le triangle ADJ
La somme des produits des résistances :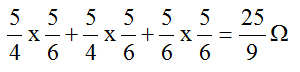
   

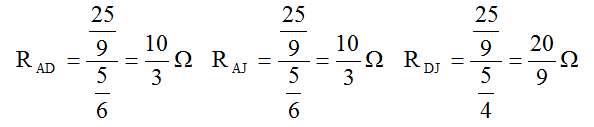
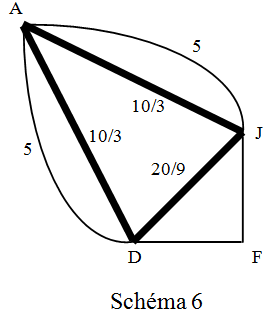
Schéma 6

Entre A et D, 5 Ω et 10/3 Ω en parallèle : RAD = 2 Ω
Entre A et J, 5 Ω et 10/3 Ω en parallèle : RAJ = 2 Ω

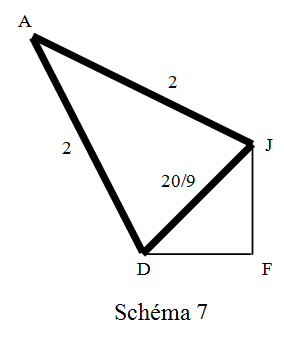
Schéma 7

On remplace le triangle ADJ par l ‘étoile OA, OD, OJ.
La somme des résistances vaut : 2+2+20/9=56/9 Ω

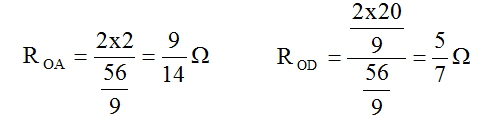
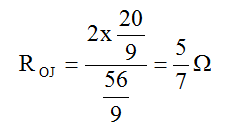
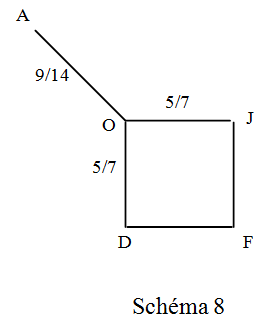
Schéma 8

OD et DF sont en série : ROF =5/7+1= 12/7 Ω
OJ et JF sont en série : R’OF = 5/7+1= 12/7 Ω

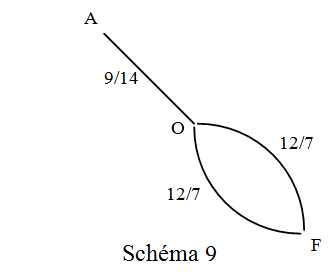
Schéma 9

Les 2 résistances entre O et F sont en parallèle : ROF = 6/7 Ω
Les résistances AO et OF sont en série : RAF = 1,5 Ω.

 

Enoncé