C’est Heinrich Gossen qui a proposé au milieu du XIXe siècle la première version d’une théorie de l’utilité. Selon lui la consommation d’une unité supplémentaire d’un bien augmente l’utilité totale ressentie par le consommateur, mais l’utilité procurée par cette dernière unité consommée est plus faible que celles procurée par l’unité précédente. Ainsi la fonction d’utilité liant quantité consommée et utilité procurée est une fonction croissante mais de moins en moins vite : on dit que l'utilité totale est croissante mais que l’utilité marginale est décroissante.
Supposer qu’un individu est capable d’attacher un indice d’utilité à la consommation d’un bien revient à dire que l’utilité est mesurable, c’est une théorie de l’utilité cardinale. C’est cette conception qui est retenue par les fondateurs de l’analyse marginaliste : Léon Walras, Carl Menger et Stanley Jevons. Conscient de l’impossiblité de mesurer directement l’utilté Vilfredo Pareto introduit la théorie de l’utilité ordinale. Dans la conception ordinale les indices doivent simplement "respecter l’ordre des préférences" pas les "mesurer".

Admettons que les trois hypothèses permettant de passer de la relation de préférence à la fonction d’utilité sont remplies (la relation de préférence est totale, réflexive et transitive). Admettons en plus que : - les quantités consommées des biens et les préférences associées peuvent varier de manière infinitésimale, c’est-à-dire continue, axiome de continuité des préférences - que toute augmentation de la consommation de l’un des produits du panier, sans diminution de la consommation des autres, augmente l’utilité de ce panier, axiome de non satiété des préférences - que pour une même utilité procurée par un panier composé d’un seul bien et un panier composé de plusieurs biens le consommateur choisira le second, axiome de la préférence pour les mélanges (ou pour la variété). 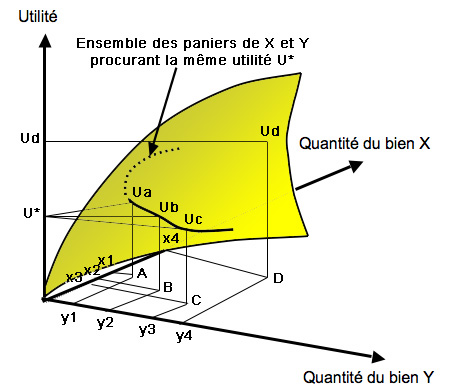Ces trois hypothèses complémentaires correspondent à trois propriétés mathématiques de la fonction d’utilité, la continuité, la monotonicité et la convexité.Sous ces hypothèses (cette axiomatique des préférences), la fonction d’utilité peut être représentée graphiquement en respectant les propriétés exigées. Dans le cas simple de paniers constitués de deux biens X et Y on a par exemple le graphique de gauche. Sur ce graphique les paniers A, B et C procurent la même utilité U*, autrement dit Ua = Ub = Uc = U*. Pour le consommateur il est indifférent de consommer A, B ou C. En revanche le panier D est préféré aux trois autres.

Cette représentation en trois dimensions est délicate, il est plus commode de s’en tenir à deux dimensions par exemple en observant tous les paniers procurant une même utilité. Graphiquement cela revient à couper l’axe vertical de la représentation en trois dimensions par un plan parallèle au repère constitué par les axes des quantités de produits. En coupant la surface représentant la fonction d’utilité par un plan pour un niveau d’utilité donné (par exemple U*) on obtient une "trace" qui donne tous les paniers "indifférents" donnant une même utilité U*.