Propriétés de la fonction d'utilité

L'idée est simple : imaginons un consommateur qui veut consommer deux biens en ayant la possibilité de mélanger comme il le veut les quantités de chacun des deux biens. Il est capable d'apprécier l'utilité procurée par la consommation de telle ou telle quantité de chacun des deux biens. Il est donc capable d'apprécier l'utilité totale associée à chaque combinaison des deux biens.
Les quantités (x₁, y₁) et (x₂, y₂) des biens X et Y donnent la même utilité : le consommateur est indifférent face au choix du panier A₁ ou du panier A₂. En mettant une quantité plus grande de bien Y dans le panier A₁ l’utilité de ce nouveau panier augmente. On peut obtenir la même utilité que celle de ce nouveau panier B₁ en modifiant le panier A₂ par une augmentation de la quantité du bien Y. Le panier B₂ correspond à un indice d’utilité plus grand que celui du panier A₂ et identique à celui du panier B₁.

Plus les courbes d’indifférence sont éloignées de l’origine des axes plus l’indice d’utilité auquel elle corresponde est élevé. Cela revient à considérer que le consommateur est insatiable, ce qui peut s’exprimer de manière "savante" - la propriété mathématique de monocité est aussi l’axiome de la non saturation des préférences – ou de manière triviale – le consommateur « veut toujours plus ».

Si les préférences sont transitives les courbes d’indifférence ne peuvent pas se couper. Un raisonnement par l’absurde permet de le montrer facilement.
Sur le graphique on voit que les paniers A₁ et A₂ sont indifférents et qu’il en va de même pour A₁ et B₂. C’est impossible car le panier B₂ a une plus grande utilité que le panier A₂ puisqu’il contient la même quantité du bien X mais une plus grande quantité du bien Y.Supposons que nous décidions de mélanger deux paniers de biens comme (x₁, y₁) et (x₂, y₂) situés sur une même courbe d’indifférence.

Si on opère le mélange en équilibrant davantage la composition du panier - plus de bien Y que dans le panier 1 et plus de bien X que dans le panier 2 on obtient des paniers qui se situent sur le segment de droite joignant les deux paniers 1 et 2. Comme tous ces points sont "au-dessus" de la courbe d’indifférence de niveau UA ils correspondent à des paniers ayant une plus grande utilité que les deux paniers 1 et 2. Le panier "mélangé" donnant la plus grande utilité dans cet exemple est (x₃, y₃).

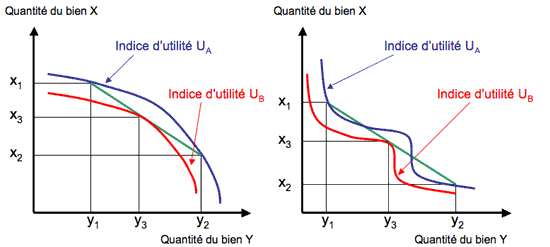
La forme des courbes se déduit de l’hypothèse de "préférence pour les mélanges" comme le troisième graphique.
Lorsque le consommateur "préfère les mélanges", les courbes d’indifférences sont forcément convexes ce qui n’est pas le cas dans ces deux exemples

Dans tout ce qui précède il y a une hypothèse implicite : les biens sont substituables. Le consommateur compose son panier de consommation en combinant des quantités des deux biens parce qu’il peut remplacer l’un par l’autre.
Cette propriété, la substituabilité peut être plus ou moins bien satisfaite, les biens peuvent être plus ou moins substituables, ils peuvent des complémentaires. La complémentarité est une caractéristique traduisant le fait que la consommation d’un bien implique celle d’un autre dans une proportion constante. .

Lorsque la subsituabilité est parfaite les courbes d’indifférence sont des droites, lorsque la substitaubilité se réduit la convexité est plus forte et lorsque la substitution disparait les courbes prennent la forme d’un L.

Supposons qu’un litre d’essence et un litre de gas-oil procurent les mêmes performances et qu’il existe un véhicule acceptant l’un ou l’autre y compris les mélanges dans n’importe quelle proprtion. Un litre de carburant est constiuté dans ces conditions de x% d’essence et de (1 - x)% de gas-oil. Le propriétaire peut substituer sans aucun problème n’importe quelle quantité d’un carburant à l’autre. S’il utilise deux litres de carburant l’utilité procurée augmente et ainsi de suite comme le montre le graphique.

Supposons maintenant que notre consommateur aime le thé et le sucre uniquement quand ils sont associés dans la proportion d’un morceau de sucre pour une tasse de thé, en dehors de cette configuration ni le sucre ni le thé ne lui procure aucun plaisir. Il lui est donc indifférent de recevoir une, deux ou trois tasses de thé s’il n’a qu’un morceau de sucre et de la même manière s’il n’a qu’une seule tasse de thé, deux ou trois morceaux de sucre ne lui procure pas plus de bien être qu’un seul. Cela signifie que le panier A (une tasse de thé et un morceau de sucre) ou le panier B (deux tasses de thé et deux morceaux de sucre) sont désirées, B étant préféré à A puisque la consommation est plus importante. Les courbes d’indifférence sont orthogonales et dessinées en pointillés pour bien montrer qu’en dehors des combinaisons telles de A et B, le consommateur n’améliore pas sa satisfaction.
Dans cet exemple, le sucre et le thé sont des biens complémentaires.

Formes des courbes d'indifférence du consommateur