On peut regrouper tous les points du réseau sur une famille de plans parallèles équidistants appelés plans réticulaires.
Un plan peut être parfaitement défini par trois points quelconques non alignés de ce plan, ces points pouvant être, par exemple,
les intersections avec les axes de coordonnées.
Mais plutôt que de repérer le plan directement par les coordonnées de ses points d’intersection avec les axes, on préfère utiliser
les indices de Miller, qui s’obtiennent de la manière suivante :
- on choisit un repère (O, a, b, c) tel que le point O soit sur un nœud du réseau,
- on trouve les abscisses des points intersections du plan avec les trois axes de vecteurs a, b et c,
- on prend l’inverse de ces valeurs et on détermine les plus petits entiers h, k et l qui sont dans le même rapport que ces inverses.

Les nombres ainsi obtenus sont les indices de Miller du plan, qui est noté (h k l).

Si le plan est parallèle à un des axes de coordonnées, son intersection est rejetée à l’infini, l’indice correspondant est nul (1/∞).
Si le plan coupe l’axe dans sa partie négative, l’indice correspondant est négatif, alors le signe moins est souvent placé au dessus
de l’indice : (h –k l) devient (h k̅ l)

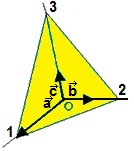
Exemple : Les intersections du plan représenté avec les axes de coordonnées a, b et c, ont respectivement pour abscisses 1, 2 et 3.
La valeur des inverses est respectivement de 1, ½, ⅓.

    Les plus petits entiers qui sont dans le même rapport que ces inverses
    sont 6, 3 et 2. Ce sont les indices de Miller du plan.
    Ce plan réticulaire sera donc noté (632).
    Il existe une infinité de plans réticulaires parallèles à ce plan.
    Cette infinité de plans contient l’ensemble des nœuds du réseau.
    Si l’on désigne cette famille par (h k l).
    Les trois entiers h, k et l sont les indices de Miller de la famille de plans
    réticulaires.
 

On peut résumer par une phrase : Les indices de Miller d’une famille de plans réticulaires sont les inverses des longueurs
découpées sur les axes par le premier plan de la famille qui ne contient pas l’origine.