Droite de régression selon les moindres carrés
Arrivé à ce stade, on peut rappeler les principales étapes de la démarche mise en place.
En étudiant une population donnée, on cherchait à déterminer si un caractère
dépendait de manière affine d'un caractère
.Graphiquement, cette recherche a conduit à celle d'une droite traduisant plus fidèlement que toute autre droite un éventuel alignement des points du nuage représentant les individus de la population étudiée.
On a alors convenu qu'une droite est (globalement) d'autant plus proche des points d'un nuage que l'écart quadratique moyen
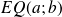par rapport à cette droite est faible.Finalement, si on trouve deux nombres
et
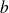tels que
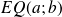soit minimal, alors on aura obtenu le coefficient directeur et l'ordonnée à l'origine de la droite la plus "proche" possible du nuage de points.
Définition :
Une telle droite, qui minimise la valeur de l'écart quadratique moyen, est appelée droite de régression de
en
au sens des moindres carrés (puisque le critère que l'on a défini repose sur une moyenne de carrés que l'on doit rendre minimale). On la note
.
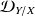On va voir, dans la suite, comment trouver de tels nombres et donc comment obtenir une telle droite de régression.
Il restera ensuite à déterminer si on peut considérer que les points du nuage sont réellement proches de cette "meilleure droite possible", et donc à conclure si les données étudiées confortent l'hypothèse d'une dépendance affine de
par rapport à
.
