T(p) = A/(1+tp)     T(jw) = A/ (1 + jwt)
çT(jw)ç = G(w) = A/(1 + w²t²)^1/2   et   ^T(jw) = j(w) = - arc tan (wt).
Quand w varie de 0 à l'infini, j(w) varie de 0 à - 90°.
Une valeur caractéristique de w :  w₀ = 1/t  est telle que   j(w₀) = - 45°.
On a alors  G(w₀) = A/2^1/2 @ 0,7A.
Le lieu de Nyquist du premier ordre est un demi-cercle.

Le lieu de Black présente une asymptote verticale à - 90°. Pour w = w₀ on a:  G_dB(w₀) = 20logA - 10log2 = A_dB - 3 dB.

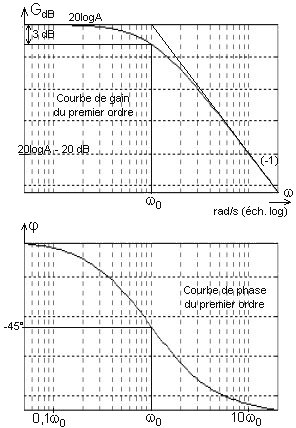
Lieux de Bode: Le diagramme asymptotique de gain est constitué, dans le domaine des basses pulsations, d'une asymptote horizontale [pente (0)] à l'ordonnée AdB = 20logA, et à partir de w = w0 d'une asymptote de pente (-1) c.à.d. -20 dB/décade. Dans le domaine des hautes pulsations, le premier ordre se comporte exactement comme un intégrateur (à partir de w = 10w0). La courbe de phase admet un centre de symétrie en w0 pour j(w0) = - 45°. A l'asymptote de pente (0) pour le gain correspond une asymptote à 0° pour la phase. A l'asymptote de pente (-1) pour le gain correspond une asymptote à (-1) fois 90°. Il y a corrélation entre la pente de la courbe de gain et la valeur du déphasage.

Identification d'un système du premier ordre par la réponse harmonique: 
 
On recherche d'abord la pulsation qui correspond à un déphasage de - 45°. La valeur de cette pulsation est w₀. Puis on règle la pulsation de la sinusoïde de commande à une valeur inférieure à w₀/10. On mesure le gain (rapport d'amplitude) pour cette pulsation. Ce gain est le gain statique A du système. Il ne reste plus qu'à prendre l'inverse de w₀ pour obtenir la constante de temps du système:  t = 1/w₀.
La fonction de transfert s'écrit alors  T(p) = A/(1+tp).