On étudie la propagation de la gauche vers la droite d'un ébranlement le long d'une corde très longue.
L'élongation de l'origine de la corde est donnée par la relation Y₀ = A.sin(ω.t). (A est l'amplitude maximum)
ω est la pulsation (ou fréquence angulaire) du mouvement.
La fréquence est égale à ν = ω / 2π et la période est l'inverse de la fréquence T = 1 / ν = 2π / ω.
Cet ébranlement se propage et tous les points de la corde sont animés d'un mouvement sinusoïdal. Considérons un point P situé à la distance x de l'origine. Son mouvement est également sinusoïdal mais il est déphasé par rapport au mouvement de l'origine de l'angle φ(x). L'élongation de P est donnée par Y(x) = A.sin(ω.t − φ).
L'examen de la corde avec un stroboscope montre que la forme de la corde est une sinusoïde et donc que φ(x) = k.x.
On peut écrire Y(x) = A.sin(ω.t − k.x) et en posant V = ω / k on obtient Y(x) = A.sin ω(t − x / V).
V a la dimension d'une vitesse. Un observateur qui se déplacerait (le point jaune du programme) à la vitesse V le long de la corde en examinant uniquement le point situé en dessous de lui verrait ce point immobile. V est donc la vitese de propagation de la phase de l'onde.
A l'instant t, la distance qui sépare deux points ayant la même élongation est λ = V.T C'est la longueur d'onde.
On définit également le nombre d'onde σ = 1 / λ et le vecteur d'onde k = 2π / λ .
Selon les problèmes étudiés on utilise l'une des formes équivalentes suivantes de l'équation de l'onde progressive :

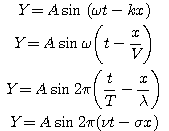
Si la propagation s'effectue de la droite vers la gauche, il faut remplacer dans ces relations les signes − par des signes + puisque V est changé en −V

Utilisation :

Cliquer dans le cadre de l'applet pour geler l'animation .

Avec les curseurs modifier l'amplitude, la pulsation est la vitesse de l'onde.
Le programme calcule et affiche les grandeurs caractéristiques de l'onde. Il trace également le segment qui correspond à la longueur d'onde.
Vérifier en stoppant l'animation que la longueur d'onde est la distance qui sépare deux points ayant la même élongation.
Le point jaune simule un observateur qui se déplace à la vitesse V au dessus de la corde.
Le trait bleu indique l'élongation du point situé à 3 m de l'origine. Pour quelles valeurs de la longueur d'onde ce point est-il en phase avec l'origine ?