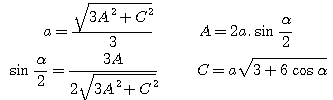Il est assez difficile d'effectuer des calculs dans une maille trigonale. Mais il est toujours possible d'associer à une telle maille une maille multiple hexagonale dans laquelle les calculs sont plus simples.
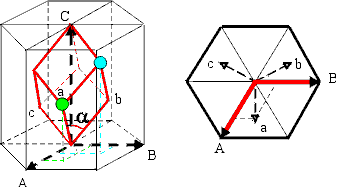
Dans la maille hexagonale caractérisée par les vecteurs de base A, B, C on ajoute au nœud origine 0, 0, 0 deux nœuds dont les coordonnées réduites sont : 2/3, 1/3, 1/3 (en vert) et 1/3, 2/3, 2/3 (en cyan sur la figure). On définit ainsi une maille trigonale dont les vecteurs de base sont a, b et c.
Dans la maille hexagonale caractérisée par les vecteurs de base A, B, C on ajoute au nœud origine 0, 0, 0 deux nœuds dont les coordonnées réduites sont : 2/3, 1/3, 1/3 (en vert) et 1/3, 2/3, 2/3 (en cyan sur la figure). On définit ainsi une maille trigonale dont les vecteurs de base sont a, b et c.
Les matrices de passage entre les deux repères (matrices également valables pour les indices de Miller des plans) sont donc :

Les paramètres des deux mailles sont donc reliés par les relations suivantes :

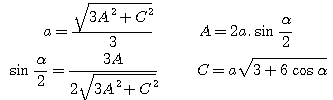
Utilisation :
Cette applet effectue la conversion des paramètres de maille  et des indices de Miller des plans réticulaires entre les réseaux trigonaux et hexagonaux.
Choisir le mode de conversion avec les cases à cocher puis taper les valeurs des paramètres de la maille (avec la valeur de l'angle "α" de la maille trigonale exprimée en degrés) et enfin cliquer sur le bouton [Conversion].
Procéder de la même manière pour les indices de Miller du plan.
Le programme affiche aussi l'équidistance des plans réticulaires de la famille h, k, l.