analyse en composantes principales

On consultera aussi le document « Introduction numérique à l’analyse en composantes principales ».

1 nature des données et Objectifs.

1.1 Nature des données.

Tableau de données quantitatives de la forme individus x variables quantitatives (ex. Euromarket) : la ligne i du tableau donne les observations X_j(i) des variables X_j sur l’individu de rang i.

N°	âge	revenu	achats	nombre d’enfants
1	51	195888	150.15	3
2	39	128456	173.12	2
3	39	117663	88.91	2

Extrait du tableau de données Euromarket

limité aux données quantitatives

1.2 Objectifs

· Formation de groupes d’individus et typologie.

· Description des relations entre des variables statistiques

2 Distance entre deux unités statistiques.

2.1 Propriétés de la distance.

· on choisit les variables dont on tient compte pour comparer les individus ;

· plus les valeurs sont différentes, plus les individus sont différents ;

· la distance entre deux individus identiques doit être nulle ;

· un changement d’unité de mesure ne doit pas changer la distance entre les individus.

2.2 Modélisation

· Les unités statistiques sont définies par les observations de p variables quantitatives ;

· On dit qu’elles appartiennent à un espace de dimension p ;

· On calcule les moyennes et les variances des p variables initiales ;

· On en déduit les valeurs centrées réduites notées x_j’(i) (1 £ i £n, 1 £ j £p) ;

· La distance entre deux unités statistiques i et i’ est donnée par son carré :

		p
d²(i,i’)	=	S	[ x_j’(i) – x_j’(i’)]²
		j = 1

3. Représentations graphiques des unités statistiques.

3.1 Recherche des axes et des plans principaux.

Définition :

Les axes principaux sont les droites déterminées au fur et à mesure de façon que :

· Les unités statistiques soient aussi proches que possible des axes suivant le critère des moindres carrés ;

· Chaque droite soit orthogonale aux précédentes.

Définition :

Les composantes principales sont les variables statistiques dont les valeurs sont les coordonnées des points sur les axes.

· Première composante principale : c₁(1), c₁(2), …, c₁(i), …c₁(n)

· Deuxième composante principale : c₂(1), c₂(2), …, c₂(i), …c₂(n)

· Etc.

Propriétés et définitions :

· les composantes principales sont centrées ;

· les composantes principales sont non corrélées deux à deux ;

· la variance d’une composante principale est appelée valeur propre.

· la somme de toutes les valeurs propres est égale au nombre de variables.

3.2 Représentation graphique.

Construction des plans principaux :

Pour représenter graphiquement les individus par des points :

· on choisit deux axes principaux, en général les deux premiers ;.

· on range les axes principaux suivant les valeurs propres décroissantes ;

· on représente chaque individu par son rang ou son identificateur placé au point dont les coordonnées sont les axes sont les composantes principales de cet individu.

Figure 1 : construction du plan principal 1 x 2

Interprétation :

· Chaque plan défini par deux axes principaux conserve une part d’information mesurée par la somme des valeurs propres correspondantes.

· Les distances entre les individus sont d’autant mieux conservées sur le plan que la somme des valeurs propres est élevée.

· L’origine des axes représente le point moyen (les moyennes de toutes les variables).

· Les plans sans axe commun contiennent des informations strictement complémentaires.

4. Interprétation des axes. Cercles de corrélation.

4.1 Cercles de corrélation.

Définition : un cercle de cercle de corrélation défini par deux composantes principales est la représentation graphique des variables en fonction de leurs coefficients de corrélation avec les composantes principales

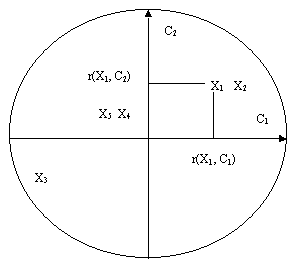
Figure 2 : construction du cercle de corrélation 1 x 2

4.2 Interprétation.

Principes :

· Un point proche du cercle caractérise bien la variable correspondante ;

· un point proche du centre indique une variable dont les propriétés ne sont pas mises en évidence par le cercle de corrélation ;

· deux points proches du cercle et l’un de l’autre indiquent une forte corrélation positive entre les variables qu’ils caractérisent (exemple X₁, X₂);

· deux points proches du cercle et opposés indiquent une forte corrélation négative (exemple X₂, X₃) ;

· deux points proches du centre du cercle ne donnent aucune indication sur la corrélation des variables qu’ils représentent (exemple X₄, X₅).

Relation avec les plans principaux :

Si une corrélation entre une variable et une composante principale est :

· fortement positive :

4 la valeur de la variable observée sur un individu dont la composante principale est positive et élevée sera vraisemblablement largement supérieure à la moyenne ;

4 la valeur de la variable observée sur un individu dont la composante principale est négative et élevée en valeur absolue sera vraisemblablement largement inférieure à la moyenne ;

· fortement négative :

4 la valeur de la variable observée sur un individu dont la composante principale est positive et élevée sera vraisemblablement largement inférieure à la moyenne ;

4 la valeur de la variable observée sur un individu dont la composante principale est négative et élevée en valeur absolue sera vraisemblablement largement supérieure à la moyenne ;

5. Compléments.

cosinus carrés : mesure de la proximité entre un point et l’individu qu’il représente

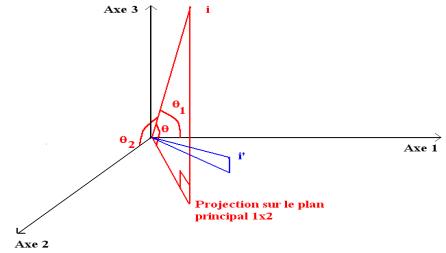
Figure 3 :Projection d’unités statistiques sur le plan principal 1 x 2.

cos²q = cos²q₁ + cos²q₂

· cos²q proche de 1 : individu proche de sa projection

· cos²q proche de 0 : individu éloigné de sa projection

La distance entre deux projections n’est proche de la distance réelle que si les deux individus sont bien représentées.

éléments supplémentaires : éléments figurant sur les représentations graphiques mais non pris en compte dans les calculs (par exemple, centre de gravité de groupes d’individus, moyennes de certaines variables, …)

6. Pratique de l’analyse en composantes principales.

L’analyse en composantes principales est une méthode statistique qui nécessite :

· une bonne connaissance des données analysées ;

· une bonne connaissance de la méthode statistique ;

· un esprit critique développé et de la prudence dans les interprétations ;

· une aptitude à rédiger de façon claire.

On procède tout d’abord par :

· une réflexion sur les données étudies en fonction de la question posée : ces données permettent-elles de répondre à cette question ?

· un examen rapide des données par les méthodes statistiques élémentaires ;

· des transformations pour « normaliser » les histogrammes (passage au logarithme, à la racine carrée à l’arc sinus ou arc tangente ...)

Avant de procéder à l’analyse en composantes principales, on réfléchit sur :

· le choix de la distance entre les individus : quelles sont les variables dont il faut tenir compte ?

· l’introduction de variables supplémentaires : ces variables ne sont pas prises en compte dans le calcul de la distance

· l’introduction d’individus supplémentaires : centres de gravité de groupes d’u.s., par ex.. Le calcul des moyennes , variances et coefficients de corrélation ne tiennent pas compte de ces u.s.

On effectue ensuite l’ACP :le logiciel donne les résultats numériques et graphiques.

· l’étude des valeurs propres permet de sélectionner les axes a priori interprétables ;

· le cercle de corrélation donne une interprétation aux axes ;

· on forme des groupes homogènes d’u.s. en expliquant les points communs ;

· on explique les propriétés structurelles des données.

En conclusion, on indique la confiance que l’on peut accorder aux conclusions de l’analyse suivant la taille du tableau, les données observées, les questions posées, les interprétations effectuées. On notera que ces conclusions ne sont pas toujours pertinentes : s’il faut s’efforcer de détecter les propriétés générales contenues dans les données, il faut inversement accepter l’absence d’informations intéressantes.