Chapitre 9

analyse
multidimensionnelle

L’analyse des données multidimensionnelles regroupe un ensemble de méthodes statistiques récentes et est utilisée couramment depuis les années 1970 environ pour analyser des clientèles, effectuer des études de marché, etc. Elles analysent des données appelées multidimensionnelles, caractérisées par le fait qu’à chaque unité statistique sont associées plusieurs valeurs observées. Ces méthodes sont fondées soit sur les mathématiques – c’est l’analyse factorielle – , soit sur l’informatique – c’est la classification qualifiée parfois d’automatique.

La complexité des calculs rend indispensable l’utilisation d’un ordinateur et de logiciels appropriés.

1. analyse en composantes principales.

1.1 Objectifs.

L’objectif de l’analyse en composantes principales (ou ACP) est purement descriptif : il s’agit « d’explorer » un ensemble d’observations rassemblées sous la forme d’un tableau de données indiquant pour chaque unité statistique les valeurs observées d’un certain nombre de variables quantitatives, comme le tableau des données Euromarket (50 lignes, 5 colonnes).

Ce tableau peut être de dimensions importantes : le nombre de lignes (d’unités statistiques) peut atteindre plusieurs centaines, et le nombre de colonnes (de variables) plusieurs dizaines. Le nombre d’observations, suivant son importance, pourra donner un caractère de généralité aux propriétés structurelles ; il est en effet rare que l’on fasse appel, dans le cadre de l’analyse de données multidimensionnelles, à la statistique inférentielle.

L’analyse en composantes principales est fondée sur le calcul des moyennes, variances et coefficients de corrélation. Les données doivent donc être quantitatives : elles peuvent être discrètes ou ordinales (par ordre de préférence).

Exemple : On étudie les données sur 50 clients de l’hypermarché EUROMARKET constituées de l’âge, du revenu, du montant des achats, du nombre d’enfants, de la catégorie socioprofessionnelle (CSP) et du sexe. Les variables quantitatives sont les suivantes : l’âge, le revenu, le montant des achats, le nombre d’enfants. Nous verrons ultérieurement comment tenir compte du sexe et de la catégorie socioprofessionnelle dans les analyses.

Nous avons étudié dans le chapitre 3 les couples d’observations (âge, revenu) en les représentant graphiquement et en calculant le coefficient de corrélation. Cette représentation graphique nous a montré que le revenu s’accroît en fonction de l’âge, jusqu’à 60 ans environ, ce que nous avons expliqué par le fait qu’au-delà de 60 ans, les clients sont en retraite et voient leurs ressources financières diminuer.

L’analyse en composantes principales généralise cette démarche en prenant en compte la totalité des variables quantitatives : ainsi, nous verrons que les personnes de 60 ans et plus n’ont en général pas d’enfant à charge, et par suite le montant de leurs achats est moins élevé : il y a donc une tendance générale dans les données, liée à l’âge, qui permet d’expliquer la diminution de la consommation de plusieurs façons.

La taille de ce tableau est insuffisante pour que les interprétations soient intéressantes. Mais elle permet de donner la totalité des résultats concernant les variables et d’effectuer des calculs sur quelques unités statistiques à l’aide d’une simple calculatrice.

1.2 Distance entre deux unités statistiques.

Un des objectifs de l’analyse en composantes principales est de grouper des unités statistiques se ressemblant suivant les variables observées et de différencier les groupes ainsi obtenus. Pour être analysée mathématiquement, cette ressemblance doit être mesurée quantitativement. Pour cela, on généralise la distance que l’on définit habituellement entre deux points du plan.

En géométrie euclidienne classique, chaque point M du plan est repéré par deux coordonnées x_M et y_M, et la distance entre deux points M et M’ a pour carré :

d²(M,M’) = (x_M - x_M’)² + (y_M - y_M’)²

En ACP, on considère chaque unité statistique comme un point repéré par ses valeurs. Si à chaque unité statistique i sont associées p valeurs x_j(i) j = 1, …, p, le point est dans un espace de « dimension p ».

Pour comparer deux unités statistiques i et i’, il est naturel de généraliser la distance précédente en considérant la somme des carrés des différences entre toutes les variables.

Exemple : voici deux clients d’Euromarket :

n°	âge	revenu	achats	enfants	CSP	sexe
1	51	195888	150.15	3	Agri.	M
2	39	128456	173.12	2	Ouv.	F

Nous cherchons à mesurer quantitativement la distance entre ces deux clients : l’impossibilité de tenir compte dans le calcul numérique de la CSP et du sexe est évidente, et nous nous limitons aux variables quantitatives. La distance habituelle est définie par son carré : elle consiste à effectuer la somme des carrés des différences entre les valeurs observées.

d²(1,2) = (51 – 39)² +(195888- 128456)² + (150.15 – 173.12)² + (3 – 2)² = 4.547 10⁹

Le deuxième terme du second membre est très élevé par rapport aux autres, que l’on peut considérer comme négligeables. Une différence d’âge de 10 ans a le même effet sur le carré de la distance qu’une différence de revenu annuel de 10F : cela ne correspond pas à la notion intuitive de la distance entre deux clients. Chaque terme du second membre est en fait dépendant de l’unité de mesure de l’observation, ce qui rend la distance sans intérêt puisque l’on n’aura pas la même valeur si les revenus sont mesurés en francs, en KF ou en euros par exemple.

La distance entre deux unités statistiques doit donc être indépendante des unités de mesure. Pour cela on la calcule sur les données centrées réduites.

Exemple : les moyennes et les écarts-types des variables sont les suivantes :

Variable	Moyenne	Écart-type
Âge	40.06	9.34111
Revenu	107639.48	29615.79478
achats	316.945	207.12912
enfant	1.82	1.03325

Les données centrées réduites sont les suivantes :

n°		âge	revenu	achats	enfants
1		51 - 40.06	195888 - 107639.48	150.15 - 316.945	3 - 1.82
		9.34111	29615.79478	207.12912	1.03325
	=	1.1712	2.9798	-0.8053	1.1420

2		39 - 40.06	128456 - 107639.48	173.12 - 316.945	2 - 1.82
		9.34111	29615.79478	207.12912	1.03325
	=	-0.1135	0.7029	-0.6944	0.1742

Le carré de la distance est ici aussi égal à la somme des carrés des différences. Il ne dépend plus des unités de mesure puisque si les revenus sont exprimés en euros et non en francs, la valeur numérique est divisée par 6.56, mais la moyenne et l’écart type aussi. Cette transformation est donc sans effet sur la valeur centrée réduite. On trouve finalement la valeur suivante :

d²(1,2) =7.784

On notera que le calcul peut être effectué de la façon suivante :

(51 – 39)²		(19588 – 128456)²		(150.15-173.12)²		(3 – 2)²
–––––––––	+	–––––––––––––––––	⁺	^{–––––––––––––––––––––}	⁺	^{–––––––––––––––}
9.34111²		29615.79478²		207.12912²		1.03325²

Cas général :

· Les unités statistiques sont définies par les observations de p variables quantitatives ; on dit qu’elles appartiennent à un espace de dimension p ;

· On calcule les moyennes et les variances des p variables initiales ;

· On en déduit les valeurs centrées réduites notées x_j’(i) (1 £ i £n, 1 £ j £p) ;

· La distance entre deux unités statistiques i et i’ est donnée par son carré :

		p
d²(i,i’)	=	S	[ x_j’(i) – x_j’(i’)]²
		j = 1

Le regroupement des unités statistiques dont les distances sont faibles devient impossible à effectuer de façon empirique dès qu’elles deviennent nombreuses. Il faut donc procéder autrement :

· Soit par un algorithme de classification, sans intervention de l’utilisateur (c’est la classification automatique, par exemple la classification ascendante hiérarchique, que nous présentons rapidement dans le paragraphe 3.3) ;

· Soit par une suite de représentations graphiques conservant au mieux l’information contenue dans les données et directement interprétables : il s’agit d’analyse factorielle.

1.3 Représentations graphiques des unités statistiques.

Pour regrouper les unités statistiques en fonction de leur distance et constituer ainsi des groupes homogènes, on utilise des représentations graphiques analogues à celles que l’on construit pour représenter des couples. Il faut donc définir le repère, c’est-à-dire l’origine, les axes et les coordonnées des u.s. sur les axes.

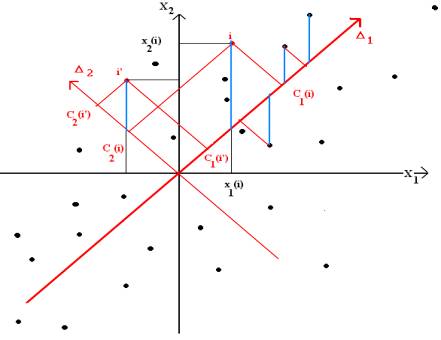
La figure 1.9 ci-dessous représente par des points les observations de deux variables centrées réduites X₁ et X₂. On choisit un système d’axes orthonormés puisque les variables sont centrées réduites. L’origine des axes est donc le point représentant une unité statistique dont toutes les valeurs centrées réduites sont nulles, ce qui signifie que toutes les valeurs initiales sont égales aux moyennes, et la longueur unité est la même sur chaque axe. Cette u.s. et le point sont qualifiés de « moyens ».

On considère la somme des carrés des distances des points à un axe D : ces distances sont les longueurs des segments représentés en rouge. L’axe qui minimise cette somme s’appelle par définition axe principal. Nous l’avons noté D₁ sur la figure 1.9.

On cherche ensuite les axes D_2,D₃, etc.

Nous n’avons représenté sur le schéma que certaines distances, mais il est bien évident qu’il est tenu compte de tous les points. On notera que ce critère est différent de celui que l’on utilise en régression (les distances considérées en régression sont représentées en bleu), et l’axe principal est en général différent de la droite de régression : on pourra visualiser ces deux droites à l’aide du programme de test du F.

Figure 1.9: Critère des moindres carré en analyse en composantes principales

représentation graphique des couples (X₁(i), X₂(i))

Ce qui se passe dans le cas général n’est pas représentable dès que le nombre de variables dépasse 3 : l’espace physique est en effet limité à trois dimensions. Mais la procédure est exactement la même, et consiste à chercher un repère dont les axes sont les plus proches possibles de l’ensemble des points caractérisés par leurs p observations x₁(i), x₂(i), …, x_p(i) (centrées réduites).

On suppose que les points sont répartis à la surface d’un ballon de rugby (figue 2.9). Ce ballon possède trois axes d’allongement maximum :

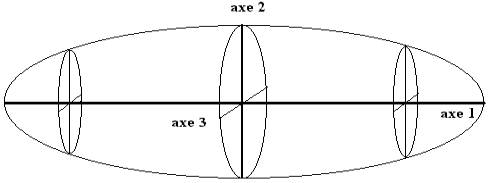
Figure 2.9 : axes principaux (espace de dimension 3)

Une fois le premier axe déterminé, on cherche le second : le critère des moindres carrés est le même, mais on impose au second axe d’être orthogonal au précédent et de passer par l’origine des axes ; dans le cas de la figure 1.9, il n’existe qu’un axe orthogonal D₂ au premier, mais en dimension trois (figure 2.9), le second axe est dans le plan orthogonal au premier axe. Le troisième, orthogonal aux deux premiers, est alors complètement déterminé par les deux précédents. Et ainsi de suite suivant le nombre de variables.

Définition :

Les axes principaux sont les droites déterminées au fur et à mesure de façon que :

· les unités statistiques soient aussi proches que possible des axes suivant le critère des moindres carrés ;

· chaque droite soit orthogonale aux précédentes.

Les axes sont ordonnés suivant la part d'information que chacun représente, mesurée par la somme des carrés des distances entre les unités statistiques qu’il permet de conserver. Cette part d'information représentée par un axe est évaluée par un paramètre appelé valeur propre et notée en général l : l’axe 1 correspond à la plus grande valeur propre l₁, l’axe 2 à la suivante l_2,etc.

On notera que les axes sont orientés de façon quelconque : deux logiciels différents peuvent donner deux axes de même rang orientés inversement l’un de l’autre sur les mêmes données, la coordonnée de chaque individu étant alors de signe opposé.

Définition : Les composantes principales sont les variables statistiques dont les valeurs sont les coordonnées des points sur les axes.

· première composante principale : c₁(1), c₁(2), …, c₁(i), …c₁(n)

· deuxième composante principale : c₂(1), c₂(2), …, c₂(i), …c₂(n)

· etc.

Les composantes principales sont obtenues comme des combinaisons linéaires des variables centrées réduites, c’est-à-dire qu’elles sont de la forme :

C_l = u_l¹ X₁ + u_l² X₂ + … + u_l^p X_p

expression dans laquelle X₁, X₂, …, X_p désignent les variables centrées réduites et u_l¹, u_l², …, u_l^p une suite de valeurs numériques possédant les propriétés suivantes :

· chaque suite u_l¹, u_l², …, u_l^p est notée u_l et est appelée vecteur propre de rang l.

· la somme des carrés u_l^{1 2} + …+u_l^p
2 est égale à 1.

· la somme des produits des termes de même rang pour deux composantes principales différentes C_l et C_k est égale à 0 :

u_l¹ x u_k¹ + u_l² x u_k² + … + u_l^p x u_k^p = 0

· les valeurs propres sont les variances des composantes principales, ou les variances des coordonnées sur les axes. Le premier axe est donc celui de la dispersion maximale des unités statistiques, le second aussi en étant orthogonal au premier etc.

Propriété : les axes principaux constituent un système d’axes orthonormés dont chacun est le plus proche des unités statistiques observées compte tenu des axes précédents. Un plan principal est un plan défini par deux axes principaux.

Exemple : la première composante principale est calculée à partir des variables centrées réduites par la formule suivante :

C₁ = 0.1200 âge - 0.3825 revenu - 0.6115 achats - 0.6822 enfants

En donnant à l’âge, au revenu, aux achats et au nombre d’enfants les valeurs centrées réduites du client de rang 1, on obtient sa coordonnée sur l’axe 1 du plan principal 1x2.

De même pour les autres clients.

Concrètement, la composante principale de rang 1 est la suite des coordonnées des clients sur l’axe 1.

Nous donnons ci-dessous la représentation graphique des 50 clients sur le plan principal 1x2. Au groupe (25, 31, 43) détecté par la représentation graphique des couples (âge, revenu) s’ajoute le client de rang 28. On peut définir un groupe opposé au précédent : (9, 11, 37, 7, 6, 45). Le client de rang 10 est assez particulier.

Le coefficient de corrélation des deux composantes principales est nul, par définition des composantes principales : il est donc impossible de distinguer une liaison linéaire sur ce plan. Par contre, dans certains cas (mais pas ici), on pourra constater une liaison non linéaire.

Figure 3.9 : plan défini par les axes principaux de rang 1 et 2 (l₁ = 1.810,l₂ = 1.290)

(certains clients sont confondus avec d’autres)

Constituer des groupes d’unités statistiques sans expliquer ce qu’elles ont en commun ne présente qu’un intérêt limité. Ces propriétés communes sont données par l’interprétation des composantes principales.

1.4 Interprétation des axes. Cercles de corrélation.

Pour caractériser les composantes principales, on calcule les coefficients de corrélation des variables initiales et des composantes principales. Ces coefficients indiquent l’intensité et la nature de la liaison entre une composante principale et les variables initiales et s’interprètent de la façon habituelle que nous avons expliquée dans le chapitre 3.

Exemple : les coefficients de corrélation des variables initiales et des composantes principales d’Euromarket sont donnés dans le tableau ci-dessous.

La corrélation entre la première composante principale d’une part, le montant des achats et le nombre d’enfant d’autre part est proche de –1 (-0.823 et –0.918) : ces valeurs numériques montrent qu’une forte valeur de cette composante principale (ce qui correspond à une coordonnée élevée sur l’axe 1, par exemple les clients 28, 25, 43 et 31) correspond à une faible valeur du montant des achats, du nombre d’enfants et du revenu dans une moindre mesure (coefficient de corrélation égal à –0.515).

	C₁	C₂	C₃	C₄
âge	0.161	0.863	-0.458	0.140
revenu	-0.515	0.707	0.436	-0.211
achats	-0.823	-0.200	-0.461	-0.266
enfants	-0.918	-0.065	0.088	0.381

Les propriétés mises en évidence par les composantes principales sont globales, vraies en général. Elles peuvent être inexactes dans des cas particuliers. Par exemple, on notera que le montant des achats du client 25 n’est pas particulièrement faible, de même que le revenu du 28.

n°	Âge	revenu	achats	enfants	CSP	sexe
25	62	76865	293.12	0	C.sup.	M
28	48	96885	63.22	0	PIC	F
31	68	86468	104.57	0	PIC	M
43	67	72999	241.78	0	Emp.	M

Pour interpréter les coefficients de corrélation, il est plus commode de les représenter graphiquement que de lire le tableau, surtout dans le cas d’un grand nombre de variables. Ces représentations graphiques s’appellent les cercles de corrélation. Un abus fréquent consiste à superposer les cercles de corrélation et les plans principaux, mais au plan mathématique, cette démarche est inexacte : la démarche exacte consiste à représenter les axes définissant les variables initiales sur les plans principaux, de la même façon qu’en figure 3.9, nous avons représenté les axes principaux dans le plan représentant les variables X₁ et X₂.

Exemple : cercle de corrélation C₁xC₂ des données Euromarket.

Ce cercle de corrélation montre que la seconde composante principale est fortement corrélée au revenu et surtout à l’âge : un client d’Euromarket dont la coordonnée est élevée sur l’axe 2 aura très vraisemblablement un âge supérieur à la moyenne et inversement. C’est le cas des n°1 et 10. On retrouve les clients n° 25, 31 et 43 dont la coordonnée élevée sur l’axe 1 montrent que le nombre d’enfants et le montant des achats sont faibles. Réciproquement, les client 9 et 37 dont les coordonnées sur l’axe 2 sont fortement négatives sont jeunes et ont un revenu faible. Rappelons que ces propriétés peuvent être inexactes sur des cas particuliers, et que l’orientation des axes peut être inversée si l’on utilise un autre logiciel.

Figure 4.9 : Cercle de corrélation C₁x C₂ (l₁ = 1.810,l₂= 1.290)

1.5 Paramètres numériques complémentaires.

Nous résumons et complétons dans ce paragraphe les résultats donnés précédemment de l’analyse en composantes principales des données Euromarket, en expliquant leur signification au fur et à mesure.

Nous donnons ci-dessous un extrait des résultats numériques concernant les unités statistiques :

n°	Axe 1	Cos²	Axe 2	Cos²	Axe 3	Cos²	Axe 4	Cos²
1	-1.286	0.135	2.822	0.653	1.569	0.202	0.350	0.010
2	0.023	0.001	0.464	0.211	0.881	0.762	0.164	0.026
3	0.411	0.123	0.309	0.069	0.917	0.614	0.514	0.193
4	1.343	0.720	-0.352	0.050	0.759	0.230	0.024	0.000
5	1.503	0.848	-0.164	0.010	0.575	0.124	0.220	0.018
…	…	…	…	…	…	…	…	…

Les lignes du tableau donnent les paramètres calculés sur chaque client.

Les colonnes intitulées Axe 1, Axe 2, … donnent les coordonnées des clients sur les axes principaux, c’est-à-dire les valeurs numériques des composantes principales.

Les colonnes intitulées Cos² contiennent un paramètre appelé cosinus carré qui indique la proximité d’un client avec le point qui le représente.

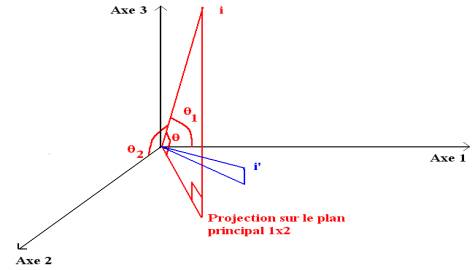
Figure 5.9 : projection d’unités statistiques sur le plan principal 1 x 2.

Le cosinus carré du client de rang 1 avec le plan 1 x 2 est égal à 0.135+0.653 = 0.788. Le cosinus de l’angle q est donc de l’ordre de 0.9, ce qui signifie que l’angle q est presque nul. On peut considérer que le client de rang est proche de sa projection sur le plan 1 x 2 représentée par le chiffre 1. C’est le cas du point i’ (figure 5.9), pour lequel nous avons :

cos²q = cos²q₁ + cos²q₂

Il n’en est pas de même du client 2 : 0.001+0.211 = 0.212. Cette valeur est faible, et le client 2 est mal représenté par sa projection sur le plan 1 x 2 : c’est le cas du point i (figure 5.9). Les unités statistiques i et i’ sont donc différentes tout en étant projetées à proximité l’une de l’autre . On notera qu’il est bien représenté sur le plan 2 x 3.

Une autre propriété générale peut être vérifiée à l’aide d’une simple calculatrice : la somme des cosinus carrés des angles entre une unité statistique et chaque axe est égale à 1. De façon analogue, la somme des carrés des coefficients de corrélation d’une variable avec chaque composante principale est égale à 1.

2. analyse des correspondances

L’analyse des correspondances est plus récente que l’analyse en composantes principales. Elle a été proposée par J-P Benzecri, professeur à l’université Paris VI, à partir des années 1965 et est très utilisée dans les sciences humaines et commerciales.

2.1 Objectifs et données.

Ses objectifs sont les mêmes que ceux de l’analyse en composante principales : c’est une méthode descriptive qui facilite la recherche de structure dans de grands ensembles de données. à l’origine, les données étudiées sont des tableaux donnant la répartition d’une population suivant deux critères qualitatifs, obtenus par exemple par tri croisé d’un ensemble de questionnaires recueillis par sondage. Elles peuvent être aussi des observations de variables quantitatives à condition toutefois qu’elles soient positives.

L’analyse factorielle des correspondances diffère de l’analyse en composantes principales par la définition des unités statistiques et de la distance utilisée pour les comparer. Dans le cas de tableaux de données quantitatives positives, c’est l’interprétation de la distance qui permet de choisir entre l’ACP et l’AFC.

Les notations utilisées dans ce paragraphe sont celles du chapitre 4 paragraphe 5.1.

Exemple : nous donnons ci-dessous un tableau obtenu par tri croisé. Le nombre de personnes interrogées est égal à la somme des termes du tableau (527) et les questions Q₁ et Q₂, comportant p = 3 et q = 4 modalités, sont les suivantes :

Q₁ : fume des cigarettes brunes, blondes, ne fume pas ;

Q₂ : mineur masculin (mm), mineur féminin (mf), majeur féminin (MF), majeur masculin (MM).

			Q₂
		mm	mf	MF	MM
	brunes	63	37	41	47
Q₁	blondes	36	55	39	38
	ne fume pas	34	27	72	38

Le test d’indépendance du c² aboutit au rejet de l’indépendance de Q₁ et Q₂ :

X² = 35.726

degré de liberté n = 6

Probabilité critique P(c²>35.726) = 0

2.2 unités statistiques.

Les unités statistiques que l’on étudie par l’analyse des correspondances sont particulières : il ne s’agit pas des personnes interrogées, mais des répartitions de leurs réponses suivant les modalités des deux questions. L’AFC complète le test d’indépendance du c² en deux variables qualitatives (cf. chapitre 6) en précisant la relation qui peut exister entre elles.

Les répartitions marginales sont obtenues par ce que l’on appelle les tris à plat. Elles donnent les pourcentages de réponses à chaque modalité de chaque question, sur le total des réponses. On note :

· P_I = (p_i.) i = 1, …, p: répartition des réponses à la question Q₁ suivant les modalités x₁, x₂, …(en proportions)

· P_J = (p._j) j = 1, …, q : répartition des réponses à la question Q₂ suivant les modalités y₁, y₂, …(en proportions)

Exemple : nous donnons ci-dessous les répartitions

· Répartition des personnes interrogées suivant qu’elles fument des brunes, des blondes ou qu’elles ne fument pas :

	brunes	blondes	non fumeurs
P_I	0.357	0.319	0.324

· Répartition des gens interrogés suivant qu’ils sont mineurs masculins, mineurs féminins, majeurs masculins, majeurs féminins :

	mm	mf	MF	MM
P_J	0.252	0.226	0.288	0.233

Les unités statistiques sont des répartitions conditionnelles, que l’on préfère souvent appeler profils : elles sont définies par les répartitions des réponses à la question Q₂ des gens qui ont donné une réponse fixée à Q₁, et inversement. On définit ainsi deux types de profils : les profils lignes et les profils colonnes. Les profils lignes sont notés P_Jⁱ et les profils colonnes P_I^j. En général, on les exprime en pourcentages, mais les calculs sont toujours effectués sur les proportions.

Ils sont affectés de poids, définis par les répartitions marginales : le poids affecté à une modalité de réponse est égal à la proportion de gens ayant choisi cette modalité dans la totalité des personnes interrogées.

Les répartitions marginales possèdent une propriété fondamentale pour l’interprétation des résultats : ce sont les centres de gravité des profils.

Exemple : Dans le tableau précédent, les profils lignes sont :

· la répartition des fumeurs de blondes suivant l’âge et le sexe ;

· la répartition des fumeurs de brunes suivant l’âge et le sexe ;

· la répartition des non-fumeurs suivant l’âge et le sexe

	mm	mf	MF	MM	total	poids
profil brunes	0.335	0.197	0.218	0.250	1	0.357
profil blondes	0.214	0.327	0.232	0.226	1	0.319
profil non fumeur	0.199	0.158	0.421	0.222	1	0.324
centre de gravité P_J	0.252	0.226	0.288	0.233	1

profils lignes P_Jⁱ

Le centre de gravité est obtenu de la façon suivante :

mm	mf	MF	MM
0.357 x 0.335	0.357 x 0.197	0.357 x 0.218	0.357 x 0.250
+ 0.319 x 0.214	+ 0.319 x 0.327	+ 0.319 x 0.232	+ 0.319 x 0.226
+ 0.324 x 0.199	+ 0.324 x 0.158	+ 0.324 x 0.421	+ 0.324 x 0.222
= O.252	= O.226	= O.288	= 0.233.

Les profils colonnes P_I^j sont :

· la répartition des mineurs masculins suivant qu’ils sont fumeurs de blondes, de brunes, ou non fumeurs ;

· la répartition des mineurs féminins suivant qu’ils sont fumeurs de blondes, de brunes, ou non fumeurs ;

· la répartition des majeurs masculins suivant qu’ils sont fumeurs de blondes, de brunes, ou non fumeurs ;

· la répartition des majeurs féminins suivant qu’ils sont fumeurs de blondes, de brunes, ou non fumeurs.

	profil mm	profil mf	profil MF	profil MM	centre de gravité P_I
brunes	0.474	0.311	0.270	0.382	0.357
blondes	0.271	0.462	0.257	0.309	0.319
non fumeur	0.256	0.227	0.474	0.309	0.324
total	1	1	1	1	1
poids	0.252	0.226	0.288	0.233

profils colonnes P_I^j

Le calcul du centre de gravité est analogue au précédent.

2.3 Notion de distance entre deux profils.

La distance utilisée pour comparer deux profils s’appelle la distance du c².

Définitions :

· La distance du c² entre deux profils lignes P_Jⁱ et P_J^i’ est définie par son carré de la façon suivante :

		q
d²(i,i’)	=	S	[ p_jⁱ – p_jⁱ’]² / p._j
		j = 1

· La distance du c² entre deux profils colonnes P_I^j et P_I^j’ est définie par son carré de la façon suivante :

		p
d²(i,i’)	=	S	[ p_i^j – p_i^j’]² / p_i.
		j = 1

Exemple : nous avons calculé les distances du c² entre les profils lignes et entre les profils colonnes du tableau de contingence précédent. Nous donnons ci-dessous le détail du calcul entre deux profils lignes :

	y₁	y₂	y₃	y₄
profil brunes	0.335	0.197	0.218	0.250
profil blondes	0.214	0.327	0.232	0.226
centre de gravité P_J	0.252	0.226	0.288	0.233

d²(x₁, x₂)	=	(0.335 –0.214)²/0.252 + (0.197-0.327)²/0.226
	+	(0.218-0.232)²/0.288 + (0.250-0.226)²/0.233

La totalité des carrés des distances entre les profils lignes et les profils colonnes sont donnés dans les tableaux ci-dessous :

	x₁	x₂	x₃
x₁	0.000
x₂	0.136	0.000
x₃	0.226	0.252	0.000

Distances entre les profils lignes

	y₁	y₂	y₃	y₄
y₁	0.000
y₂	0.192	0.000
y₃	0.264	0.325	0.000
y₄	0.037	0.109	0.128	0.000

Distances entre les profils colonnes

L’usage de la distance du c² pour comparer les profils est justifié par ses propriétés mathématiques, en particulier par les propriétés suivantes :

Propriétés de la distance du c² :

Soit X² la statistique utilisée dans le test d’indépendance du c² de Pearson et N la somme du tableau (cf. chapitre 6, paragraphe 3.2). On admettra les propriétés suivantes :

· La moyenne des carrés des distances au centre de gravité pondérés par les poids des profils est égale à X²/N ;

· La moyenne des carrés des distances entre les profils pondérés par le produit de leurs poids est égale à X²/N.

Exemple : le détail des calculs pour vérifier numériquement la seconde propriété dans le cas des profils lignes est donné ci-dessous :

p₁. p₂. d²(1,2)	+ p₁. p₃. d²(1,3)	+ p₂. p₃. d²(2, 3)	= X²/N
0.357 x 0.319 x 0.136	+ 0.357 x 0.324 x0.226	+ 0.319 x 0.324 x 0.252	= 35.726 / 527

2.4 Description d'un ensemble de profils. Définitions.

La description de chaque ensemble de profils est effectuée comme en analyse en composantes principales. On recherche les axes les plus proches des points au sens de la distance du c², et sous contrainte d’orthogonalité. Les coordonnées sur ces axes définissent des variables appelées ici souvent facteurs au lieu de composantes principales, et les variances de ces variables sont appelées valeurs propres, ou encore inerties expliquées.

Définitions et propriétés :

· Les facteurs principaux sont les composantes principales ;

· ils sont centrés et non corrélés deux à deux ;

· la variance d’un facteur, appelée inertie expliquée par l’axe, est égale à la valeur propre associée.

· le nombre de valeurs propres non nulles est inférieur ou égal au nombre de lignes moins un et au nombre de colonnes moins un.

La somme des inerties est égale à X²/N : l’analyse factorielle des correspondances apparaît ici comme une décomposition de la statistique X² utilisée dans le test d’indépendance : chaque axe principal caractérise une certaine liaison, indépendante des autres, dans l’ordre des valeurs propres croissantes.

Une différence importante avec l’analyse en composantes principales est la pondération des profils. Il est fréquent de compléter les résultats numériques associés à chaque profil par un critère tenant compte de cette pondération, appelé « contribution relative à l’inertie », qui mesure l’importance du profil dans l’inertie expliquée par l’axe (la variance).

Considérons par exemple les profils lignes. Leurs coordonnées sur l’axe l étant notées c_l(i) i = 1, …, p , on a d’après les propriétés précédentes :

	p
l_l =	S	p_i. c_l(i)²
	i = 1

La contribution relative du profil P_Jⁱ à l’inertie expliquée par l’axe est par définition le rapport p_i. c_l(i)² / l_l exprimé en général en pourcentage. La somme de ces pourcentages doit être égale à 100% pour chaque facteur.

Exemple : nous donnons ci-dessous les résultats numériques de l’analyse factorielle des correspondances du tableau de contingence:

			axe 1			axe 2
	poids	C(i)	Cos²(i)	Contrib(i)	C(i)	Cos²(i)	Contrib(i)
brunes	0.357	-0.128	0.331	12.9	-0.181	0.669	51.4
blondes	0.319	-0.168	0.449	20.0	0.186	0.551	48.2
ne fume pas	0.324	0.305	0.997	67.1	0.017	0.003	0.4

Coordonnées des profils lignes

			axe 1			axe 2
	poids	C(j)	Cos²(j)	Contrib(j)	C(j)	Cos²(j)	Contrib(j)
mm	0.252	-0.131	0.286	9.7	-0.207	0.714	47.5
mf	0.226	-0.226	0.513	25.7	0.220	0.487	48.0
MF	0.288	0.316	0.980	64.1	0.045	0.020	2.5
MM	0.233	-0.030	0.312	0.5	-0.044	0.688	2.0

Coordonnées des profils colonnes

On pourra vérifier toutes les propriétés des facteurs données ci-dessus à l’aide d’une simple calculatrice.

2.5 Représentation graphique simultanée.

Les deux ensembles de profils, étudiés jusqu’ici séparément, sont liés en fait par une relation de dualité qui facilite l’interprétation des facteurs. Cette relation est définie par les propriétés suivantes :

· les valeurs propres calculées dans chaque ensemble de profils sont égales ;

· les facteurs d’un ensemble de profils sont liés aux facteurs de l’autre.

La seconde propriété permet de représenter sur un même graphique les plans principaux des deux ensembles de profils et d’interpréter la proximité et l’éloignement de deux points caractérisant l’un un profil ligne, l’autre un profil colonne.

Exemple : nous avons représenté les profils lignes et colonnes dans un système d’axes orthonormés caractérisant les facteurs principaux. L’origine des axes caractérise les points moyens, c’est-à-dire les répartitions marginales du tableau.

Nous avons caractérisé les profils par des abréviations pour interpréter le graphique :

· mm et mf désignent respectivement les mineurs masculins et féminins

· MM et MF désignent respectivement les majeurs masculins et féminins

· brunes désigne les fumeurs de brunes

etc.

Figure 6.9 : Plan principal 1x 2 (l₁ = 0.045) axe vertical 2 (l₂ = 0.023)

On ne doit pas oublier que les comparaisons utilisent les répartitions marginales comme références. En particulier, lorsqu’une répartition marginale est déséquilibrée, il est indispensable d’en avoir bien mémorisé les propriétés avant d’effectuer les interprétations.

On peut interpréter les distances entre les profils lignes de la même façon qu’en analyse en composantes principales. De même pour les distances entre les profils colonnes. La dualité entre les deux ensembles donne l’interprétation de la proximité entre un profil ligne et un profil colonne. Ainsi :

· dans le profil blondes, la modalité mineur féminin est plus fréquente qu’en moyenne, les modalités mineur masculin et majeur féminin moins fréquentes ;

· dans le profil majeur masculin, la répartition entre fumeurs de brunes, fumeurs de blondes et non fumeurs est proche de la répartition dans la population, avec une proportion légèrement supérieure pour les brunes ;

· il y a un nombre relativement important de femmes majeures parmi les non-fumeurs, et inversement relativement peu de fumeurs de blondes ou de brunes.

On peut vérifier ces interprétations sur les tableaux des profils, en comparant aux centres de gravité correspondants.

3. Autres méthodes.

Il existe beaucoup d’autres méthodes d’analyse de données multidimensionnelles : analyse canonique, analyse factorielle des correspondances multiples, … Nous en présentons rapidement deux autres fréquemment utilisées en techniques de commercialisation : l’analyse factorielle discriminante et la classification.

3.1 Analyse factorielle discriminante.

L’analyse factorielle discriminante établit la relation entre les groupes d’unités statistiques définis par une variable qualitative et plusieurs variables quantitatives. Elle présente la particularité de proposer une règle de classement des unités statistiques.

Exemple : nous avons constitué trois groupes de clients d’Euromarket : les clients sans enfants (groupe 1), les familles classiques ayant 1 ou deux enfants (groupe 2) et les familles nombreuses (3 ou 4 enfants). La question à laquelle l’analyse factorielle discriminante permet de répondre concerne la liaison entre les groupes de famille (sans enfants, classiques, nombreuses), et les variables quantitatives observées (revenu, montant des achat, âge). L’objectif final est d’affecter un client supplémentaire à un groupe de familles suivant ses caractéristiques.

La méthodologie est fondée sur la décomposition de la variance lorsque les unités statistiques sont réparties en plusieurs groupes. C’est une propriété que nous avons déjà vue précédemment (chapitre 7, paragraphe 2.2), que nous rappelons rapidement :

Soit X une variable statistique observée sur n unités statistiques réparties en k groupes I₁, I₂, …, I_l, … I_k., d’effectifs n₁, n₂, …, n_l, … n_k. Le nombre total d’observations est égal à n :

n = n₁ + n₂ + … + n_l + … n_k

On note m et s² la moyenne et la variance de la variable X dans la totalité de la population et m₁, m₂, …, m_l, …, m_k et s₁², s₂², …, s_l², …, s_k² dans chaque groupe. On a alors les relations ci-dessous :

–––

n_l m_l

s²

–––

n_l (m_l – m)²

–––

n_l s_l²

l = 1

La seconde formule exprime la variance totale (s²) comme la somme de la variance « inter » (premier terme : variance des moyennes pondérées) et de la moyenne des variances « intra » (second terme).

Lorsque les groupes sont très différents les uns des autres, la variance inter est élevée relativement à la variance totale, et les variances intra sont faibles, ce qui signifie qu’au sein d’un groupe donné, les unités statistiques sont proches de la moyenne de ce groupe. Inversement, si les groupes sont mélangés, cela signifie que les moyennes sont relativement proches les unes des autres, et que les observations d’un même groupe sont fortement dispersées. On mesure cette « discrimination » par le rapport de corrélation :

Définition : on appelle rapport de corrélation le rapport de la variance inter à la variance totale.

Ce rapport est toujours compris entre 0 et 1. Ses propriétés sont les suivantes :

· plus il est proche de 1, plus la variance inter est élevée, plus les variances intra sont faibles (par rapport à la variance totale) et plus forte est la discrimination.

Figure 7.9 : rapport de corrélation proche de 1, bonne discrimination

· plus il est proche de 0, plus la variance inter est faible, plus les variances intra sont élevées, et moins la discrimination est forte.

Figure 8.9 : rapport de corrélation proche de 0, mauvaise discrimination

Pour en apprécier la taille, on peut l’interpréter approximativement comme le carré d’un coefficient de corrélation linéaire (il existe un test d’égalité à 0 fondé sur la loi de Fisher Snedecor).

Cette propriété est vraie quelle que soit la variable quantitative considérée X. Lorsque l’on dispose de plusieurs variables X₁, X₂, …, X_j, …, X_p que l’on suppose centrées réduites, on peut donc considérer l’ensemble des variables Y de la forme :

Y =u₁ X₁ + u₂ X₂ + … + u_j X_j + … + u_p X_p

les coefficients u₁, u₂, …, u_j, …, u_p étant des nombres réels quelconques.

L’analyse factorielle discriminante consiste à chercher ces coefficients de façon que le rapport de corrélation de Y soit le plus élevé possible. Les valeurs moyenne de cette variable Y calculées dans chaque groupe sont les plus dispersées possible au sens de la variance (inter) et inversement les valeurs de Y prises par les unités statistiques de chaque groupe sont concentrées autour de la moyenne de ce groupe (variance intra). La discrimination est maximale. On détermine ainsi la première composante discriminante, dont le rapport de corrélation est appelé pouvoir discriminant.

On cherche ensuite une autre suite de coefficients maximisant le rapport de corrélation, de façon que la seconde composante discriminante soit non corrélée à la précédente et ainsi de suite.

On trouve un nombre de composantes discriminantes inférieur ou égal au nombre de groupes diminué de 1. Parmi ces composantes discriminantes, on ne considère en général que les premières (2 ou 3). Et c’est à l’aide de ces composantes discriminantes que l’on classe les unités statistiques.

3.2 Exemple d’analyse factorielle discriminante.

Les familles clientes d’Euromarket étant réparties en trois groupes suivant le nombre d’enfants, le nombre d’axes discriminants est égal à 2, et la représentation du plan discriminant 1 x 2 est donnée en figure 6.9, chaque client étant représenté par le groupe auquel il appartient.

Le pouvoir discriminant de la première composante discriminante (0.52) n’est que légèrement supérieur au rapport de corrélation du montant des achats (0.46), auquel elle est fortement corrélée (0.893). Celui de la seconde reste relativement élevé (0.25).

On a également représenté les centres de gravité G₁, G₂ et G₃ de ces groupes en éléments supplémentaires – c’est-à-dire qu’ils n’ont pas été pris en compte dans le calcul des axes discriminants.

Figure 9.9 : plan discriminant 1 x 2

On note que le groupe 1 est nettement plus âgé en moyenne que les deux autres, que son revenu est légèrement plus faible et que c’est le montant des achats qui différencie le plus le groupe 2 (un ou deux enfants) du groupe 3 (trois ou quatre enfants). On notera que les composantes discriminantes, toujours non corrélées, ne sont pas ici indépendantes : on distingue une liaison non linéaire sur la figure 9.

	effectif	âge	revenu	achats
Groupe 1	6	50.67	87 383.8	209.2233
Groupe 2	31	38.90	107 314.4	238.4945
Groupe 3	13	37.92	117 763.5	553.7369

Moyennes des variables par groupes

(centres de gravité)

La règle d’affectation d’un client à un groupe est la suivante :

· on calcule la distance du client aux centres de gravité des groupes G₁, G₂, G₃.

· on affecte le client au groupe dont le centre de gravité est le plus proche.

On note alors quelques cas particuliers, indiqués par leur rang en italique dans la figure 7.9 : le client 32 appartient au groupe 1, le 8 appartient au groupe 2, le 26 appartient au groupe 3.

D’une façon plus générale, on calcule le tableau donnant la répartition des clients suivant le groupe auquel ils appartiennent (en ligne) et le groupe auquel ils sont affectés (en colonne) :

	1	2	3
1	4	1	1
2	1	28	2
3	0	3	10

Tableau de classement appartenance x affectation

· Sur les six clients du groupe 1, quatre sont bien classés, un est classé dans le groupe 2 et un dans le groupe 3.

· Sur les trente-et-un clients du groupe 2, l’un est classé dans le groupe 1, deux dans le groupe 3.

· Sur les treize clients du groupe 3, trois sont classés dans le groupe 2.

On calcule fréquemment pour résumer ce tableau le pourcentage de bien-classés, égal ici à 84%.

Considérons maintenant un client X âgé de 38 ans, dont le revenu est de 80000F et qui a dépensé 357F. L’analyse discriminante propose de l’affecter dans l’un des trois groupes en fonction de sa distance aux centres de gravité de chaque groupe :

Groupe 1 : 2.601287

Groupe 2 : 0.9520697

Groupe 3 : 3.235366

Ce client est beaucoup plus proche du centre de gravité du groupe 2 que des autres : il a vraisemblablement, d’après l’analyse, un ou deux enfants.

Cette analyse demande toutefois une grande prudence : le nombre d’unités statistiques doit être élevé (50 est la plupart du temps très insuffisant), le nombre de variables faible, et la règle d’affectation à un groupe est discutable.

L’analyse discriminante, comme la régression linéaire, donne des résultats dont la validation est indispensable. Il existe plusieurs façons de contrôler les résultats. La plus simple est d’appliquer la règle choisie sur un échantillon test permettant de comparer le groupe d’affectation au groupe auquel l’u.s. appartient effectivement : il faut disposer pour cela d’un effectif suffisant. Une autre façon est de calculer le pourcentage de bien classés en cas d’affectation aléatoire : on trouve ici 33% en affectant chaque u.s. à un groupe avec la probabilité 1/3. Notons qu’en affectant systématiquement les u.s. au groupe 2 et si les proportions de l’échantillon sont respectées dans la population, le pourcentage de bien classés est égal à 28/50 x 100% = 56%. Ce pourcentage ne mesure donc pas la validité de la règle de façon satisfaisante. C’est pourquoi on peut procéder enfin à une chaotisation de l’échantillon de calcul : on tire au hasard les groupes auxquels sont censés appartenir les observations, et, après avoir effectué l’analyse, on détermine le pourcentage de bien classés. Si ce pourcentage reste du même ordre qu’avec les groupes réels, c’est que la discrimination n’est pas satisfaisante. Nous avons effectué dix fois cette chaotisation et trouvé les pourcentages suivants : 38%, 6%, 24%, 8%, 42%, 24%, 50%, 44%, 24%, 32%. Le pourcentage de 80% est donc satisfaisant (on pourrait augmenter le nombre de chaotisations).

La règle de décision utilisée précédemment est élémentaire : elle n’est justifiée que sous des hypothèses contraignantes (matrice de covariances des groupes constantes). On préfère souvent utiliser comme règle d’affectation l’une de celles que nous donnons dans le paragraphe suivant. On consultera aussi l’application « vers d’autres règles de décision. »Les tests statistiques ne peuvent être utilisés que si les variables considérées suivent la loi normale (ce qui n’est pas le cas dans le fichier EUROMARKET).

3.3 Classification et règles d’affectation.

La classification rassemble des procédures surtout informatiques totalement différentes des analyses factorielles précédentes. Le modèle mathématique est beaucoup moins développé, et les difficultés des méthodes sont surtout algorithmiques et informatiques.

Toutes les procédures de classification suivent la même démarche :

· on compare des objets, qui peuvent être des unités statistiques ou des variables ;

· on définit une notion de distance, qui généralise la notion utilisée en analyse factorielle ;

· on choisit une règle d’affectation d’un objet à un groupe d’objets pour créer des groupes homogènes.

La notion de distance est fréquemment appelée dissimilarité, parce qu’elle ne vérifie pas nécessairement les hypothèses d’une distance mathématique. Les hypothèses qu’elle doit vérifier sont les suivantes :

· la dissimilarité d’un objet à un autre est positive ou nulle ;

· la dissimilarité d’un objet à lui-même est nulle.

Pour rassembler les objets qui se ressemblent, il faut définir la distance entre un objet et un groupe et plus généralement entre deux groupes d’objets. Plusieurs choix pour définir la dissimilarité entre deux groupes sont possibles, parmi lesquels (figure 10.9) :

· la distance la plus petite entre deux objets pris dans chaque groupe ;

· la distance la plus grande entre deux objets pris dans chaque groupe ;

· la distance moyenne entre les objets pris dans chaque groupe ;

· la distance entre les centres de gravité.

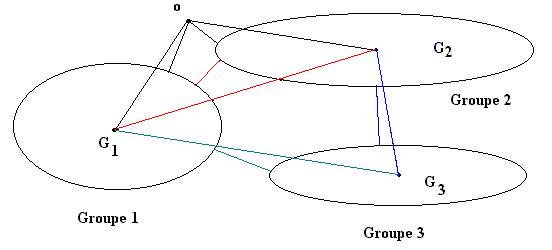
Figure 10.9 : disance entre un objet o et des groupes

distance entre deux groupes

On observe la diversité des proximités suivant le critère choisi ) : l’objet o est affecté au groupe 1 (distance au centre de gravité) ou au groupe 2 (groupe de l’objet le plus proche).

La procédure consiste alors à calculer les distances entre tous les objets, à grouper les deux objets les plus proches pour en constituer un autre qui les remplace, et à recommencer jusqu’à l’obtention d’un seul groupe constitué de tous les objets.

En figure 10.9, suivant la règle choisie, les groupes G₂ et G₃ sont réunis (distance entre les centres de gravité), ou G₁ et G₂ (suivant le plus proche voisin).

La liberté qui est laissée dans le choix de la distance se paie, et la représentation graphique des objets conformément à leurs distances réciproques peut être difficile. En particulier, il n’est pas toujours possible de les représenter géométriquement dans un système d’axes. On utilise souvent pour effectuer cette représentation une arborescence, que l’on appelle aussi dendogramme, analogue à l’arbre de classification des espèces bien connu en biologie.

3.4 Exemple.

Nous avons effectué la classification des clients d’Euromarket en considérant comme distance entre deux clients celle qui est définie par la somme des carrés des différences des variables centrées réduites, comme en analyse en composantes principales, et en choisissant comme critère d’agrégation le critère de minimisation de la variance.

Le dendogramme que l’on obtient est donné en figure 11.9. Il peut être utilisé pour classer les clients en un nombre de groupes fixé, par une procédure appelée troncature. Par exemple, pour un nombre de groupes égal à 4, on obtient la partition suivante :

Classe n° 1	1	8	10	12	25	27	31	39	43
Classe n° 2	2	3	14	16	17	19	21	23	24	26	33	34	35	36	38	41	42	44	47
Classe n° 3	4	5	13	18	2	22	28	29	3	32	4	48	49	5
Classe n° 4	6	7	9	11	15	37	45	46

Partition en 4 classes

Les groupes obtenus n’apparaissent guère sur le plan principal que nous avons donné en figure 3.9. La distance considérée est la même, mais sur ce plan n’apparaissent que les distances reconstruites par les deux premiers axes : cela explique la différence.

Cela explique aussi que souvent, on préfère effectuer cette classification sur les composantes principales ou les facteurs préalablement sélectionnés. On retrouve des groupes cohérents avec l’analyse factorielle.

Figure 11.9 : dendogramme des clients d’Euromarket

(distance euclidienne sur les données centrées réduites,

agrégation suivant la variance minimale)

conclusion

Nous avons présenté dans ce chapitre les méthodes d’analyse multidimensionnelle les plus fréquemment utilisées en France. Il en existe beaucoup d’autres, comme l’analyse des correspondances multiples, l’analyse canonique, que nous appliquons dans des études de cas figurant dans les applications pédagogiques. Ces deux dernières méthodes sont assez particulières : l’analyse des correspondances multiples, très utilisée dans les dépouillements d’enquête, donne des résultats souvent bien difficiles à interpréter de même que l’analyse canonique pourtant fréquemment utilisée aux États-Unis et au Royaume-Uni.

Le développement de ces méthodes, au plan méthodologique comme au plan numérique, suit celui de l’informatique. Les données que l’on pouvait analyser sur des systèmes informatiques puissants des années 1970 peuvent maintenant être traitées sans difficulté sur un micro-ordinateur, et de nombreuses méthodes, nécessitant une puissance de calcul de plus en plus importante, apparaissent régulièrement. On peut citer deux tendances au plan méthodologique : l’analyse de tableaux multiples, par exemple un même tableau échelonné dans le temps (J. Pagès, B. Escofier) et l’analyse de données textuelles (F. Lebart).

La facilité avec laquelle on peut effectuer une analyse multidimensionnelle présente des inconvénients : elle cache la complexité de la méthode statistique et réduit l’analyse scientifique des données préalable à l’analyse statistique. On pourra lire le texte « L’illusion du savoir » sur les problèmes posés par l’influence de la démarche scientifique sur les sciences humaines dans la rubrique Articles du site SMASH.