Chapitre 8
analyse des séries
chronologiques
Nous abordons dans ce chapitre l’analyse de données statistiques particulières en ce sens que les observations sont régulièrement échelonnées dans le temps. Ce genre de données est bien connu en économie : la quasi-totalité des indices de prix, de production etc. sont calculés régulièrement par l’INSEE ou d’autres établissements et constituent ce que l’on appelle des séries chronologiques. Elles sont fréquentes aussi en gestion : surveillance du niveau des stocks, suivi des ratios d’une entreprise etc.… Leur particularité vient de l’introduction du temps dans l’analyse de ces données : on étudie une suite de couples de la forme (t, xt), où xt est l’observation de la variable à l’instant t.
1. Description d'une série chronologique.
On distingue en général trois effets constitutifs d’une série chronologique :
· Un effet à long terme, appelée tendance (on ajoute parfois à long terme), composante tendancielle ou trend ;
· Un effet dit saisonnier, qui réapparaît à intervalles réguliers ; cet effet se traduit par une composante de la série appelée composante saisonnière.
· Un effet inexpliqué : cet effet, que l'on suppose en général dû au hasard, se manifeste par des variations accidentelles.
Dans les séries économiques longues, on cite souvent un effet supplémentaire : c'est ce que l'on appelle le cycle de Kondratiev, qui résulte du fait que, suivant la théorie de Kondratiev, à une période de prospérité économique succède mécaniquement une période de dépression.
1.1 Description de la tendance.
La description initiale de la tendance repose sur l'interprétation de la représentation graphique de la série.
Définition : on appelle tendance (ou variation à long terme ou trend) de la série xt la série ct résultant de la totalité des effets permanents auxquels est soumise la série xt.
Exemple : Nous donnons ci-dessous les cours (en €) du titre Alcatel de code sicovam 13000 du 4 janvier (n°1) au 5 mars 1999 (n°45). L'unité de temps est le jour boursier, et le cours est déterminé par l’offre et la demande elles-mêmes déterminées par l’évolution économique. Les données figurent sur le site (paramètres Alcatel.par) :
|
1 |
109.500 |
10 |
103.750 |
19 |
100.100 |
28 |
94.000 |
37 |
99.950 |
|
2 |
113.200 |
11 |
105.400 |
20 |
101.800 |
29 |
94.600 |
38 |
103.150 |
|
3 |
119.700 |
12 |
101.175 |
21 |
102.450 |
30 |
96.425 |
39 |
101.250 |
|
4 |
122.350 |
13 |
101.100 |
22 |
100.600 |
31 |
94.025 |
40 |
98.450 |
|
5 |
122.900 |
14 |
100.150 |
23 |
99.200 |
32 |
95.350 |
41 |
97.550 |
|
6 |
118.250 |
15 |
96.050 |
24 |
99.200 |
33 |
94.175 |
42 |
100.000 |
|
7 |
113.550 |
16 |
96.950 |
25 |
94.375 |
34 |
96.600 |
43 |
107.050 |
|
8 |
107.700 |
17 |
101.000 |
26 |
96.350 |
35 |
97.250 |
44 |
112.900 |
|
9 |
107.400 |
18 |
103.000 |
27 |
97.250 |
36 |
98.500 |
45 |
117.400 |
Tableau 1.8 : Cours du titre Alcatel du 4 janvier 1999 au 5 mars 1999
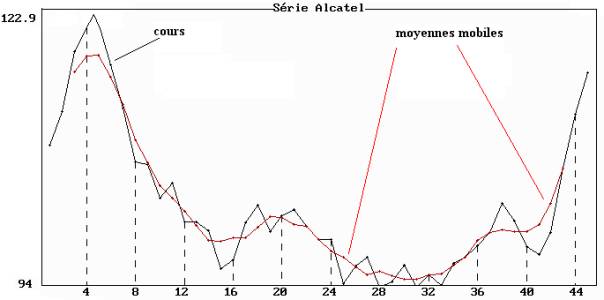
La tendance peut être décomposée en trois phases (figure 1.8) :
· Le cours baisse du début des observations (7 janvier ) jusqu'à l'observation n°15 (c'est-à-dire le 22 janvier) ;
· De l'observation n°16 (25 janvier) à l'observation n°41 (1er mars), le cours diminue légèrement ;
· Il augmente rapidement à partir du 2 mars.
On ne distingue pas sur la figure 1.8 de variations apparaissant à intervalles réguliers : la série n'est soumis à aucun effet saisonnier visible. La composante accidentelle est visualisée par les petites variations de cours d'un jour à l'autre. Par exemple le cours n°11 est supérieur au cours n°10 : cela ne remet pas en cause la baisse de la tendance compte tenu des cours du 7 au 22 janvier.

Figure 1.8 : cours journalier du titre Alcatel
(du 4 janvier 1999 au 5 mars 1999)
Pour faire apparaître plus clairement la tendance, il faut atténuer la composante accidentelle. On utilise pour cela les moyennes mobiles définies de la façon suivante :
· on appelle moyenne mobile centrée de longueur impaire li = 2 k +1 à l’instant t la valeur moyenne mmt des observations xt-k, xt-k+1, …, xt, xt+1, …, xt+k :
mmt = (xt-k + …+ xt-1 + xt
+ xt+1 + … + xt+k) / li
· on appelle moyenne mobile centrée de longueur paire lp = 2 k à l’instant t la valeur moyenne mmt des observations xt-k, xt-k+1, xt-k+2, xt, xt+1, …, xt+k , la première et la dernière étant pondérées par 0.5 :
mmt
= (0.5 xt-k + xt-k+1
+ … + xt-1 + xt + xt+1 + … + xt+k-1+ 0.5 xt+k)
/ lp
Dans la première formule, le nombre de termes de la somme est égal à 2 k + 1 : il s'agit bien d'une moyenne. Dans la seconde, la somme des coefficients est égale à 2 k, puisque le premier et le dernier sont égaux à 0.5 : il s'agit d'une moyenne pondérée. Dans les deux cas, le nombre d'observations prise en compte avant l’instant t est égal au nombre d'observations prises en compte après l’instant t : c’est pour cela que les moyennes sont dites centrées.
La première valeur d’une moyenne mobile de longueur 4 ( = 2 x 2) ou 5 (= 2 x 2 + 1) que l’on peut calculer, est à l’instant t = 3, puisque la première observation connue est x1 :
|
mm3 = (0.5 x1 + x2 + x3 + x4 + 0.5 x5) / 4 |
(l = 4) |
|
mm3 = (x1 + x2 + x3 + x4 + x5) / 5 |
(l = 5) |
De façon générale, ne peut calculer de moyenne mobile en t = 1, t = 2, …, t = k puisque les formules ne peuvent être appliquées que si l'on connaît xt-k. De même, si T est le nombre total d'observations, on ne peut calculer mmT, … mmT-k+1 puisqu'il faut connaître xt+k.
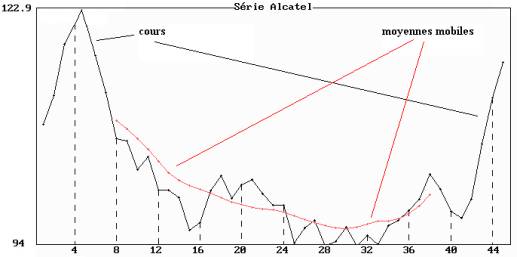
L’avantage des moyennes mobiles est d'atténuer la composante accidentelle tout en conservant les tendances linéaires : la série est dite « lissée », et est d'autant plus lissée que la longueur de la moyenne mobile est élevée comme on peut le constater sur la figure 3.8 sur laquelle nous avons représenté les moyennes mobiles de longueur 14.
Exemple : nous donnons dans le tableau 2.8 un extrait des moyennes mobiles de longueur 5 et les représentations graphiques sur les figures 2.8 et 3.8 des cours du titre Alcatel et des moyennes mobiles de longueur 5 et 14.
|
Instant |
cours (€) |
moyenne mobile |
Instant |
cours (€)€ |
moyenne mobile |
|
1 |
109.50000 |
|
42 |
100.00000 |
103.19000 |
|
2 |
113.20000 |
|
43 |
107.05000 |
106.98000 |
|
3 |
119.70000 |
117.53000 |
44 |
112.90000 |
|
|
4 |
122.35000 |
119.28000 |
45 |
117.40000 |
|
Tableau 2.8 : cours du titre Alcatel du 4 janvier (n°1) au 5 mars 1999 (n°45)
moyennes mobiles de longueur 5 (extrait)
On notera que, dans les journaux financiers, les moyennes mobiles ne sont pas centrées : on utilise les moyennes des 50 ou 100 dernières observations avant l’instant t pour définir la tendance à l’instant t.
L'inconvénient des moyennes mobiles de longueur 14 est qu’elles ne sont définies qu'à partir de la 8e observation et jusqu’à la 38e. On ne dispose d'aucune information sur la tendance ni au début ni à la fin de la période d'observation. Il faut donc choisir la longueur des moyennes mobiles suivant le nombre d'observations et l'objectif de l'analyse. Nous verrons que la longueur de ces m.m. dépend aussi de la période des variations saisonnières pour faire apparaître la tendance.
Figure 2.8 : cours du titre Alcatel du 4 janvier au 5 mars 1999
Moyennes mobiles de longueur 5.
Figure 3.8 : cours du titre Alcatel du 4 janvier au 5 mars 1999
Moyennes mobiles de longueur 4.
Théorème : si la tendance d’une série chronologique xt est linéaire et a pour équation ct = b t + a, les moyennes mobiles centrées ont pour tendance la même droite et en sont d’autant plus proches que la longueur des moyennes mobiles est élevée.
Ce théorème est démontré dans un complément pédagogique. Il peut être complété par l’étude de tendance de la forme ct = b2t2 + b1t + a proposée en application pédagogique.
1.2 Description simultanée des variations saisonnières et de la tendance.
Une variation saisonnière est caractérisée par le fait qu'elle se produit à intervalles de temps réguliers, d'où d'ailleurs le terme saisonnier.
Définition : on appelle variation saisonnière d'une série chronologique à l’instant t une variation due à un effet momentané se reproduisant régulièrement dans le temps.
Exemple : nous étudions la série
chronologique suivante observée trimestriellement pendant 6 ans (tableau 3.8).
|
|
1er trimestre |
2e trimestre |
3e trimestre |
4e trimestre |
|
Année 1 |
89.658 |
97.593 |
108.906 |
114.157 |
|
Année 2 |
96.205 |
99.399 |
112.763 |
119.185 |
|
Année3 |
99.602 |
105.192 |
116.556 |
121.911 |
|
Année 4 |
103.272 |
109.644 |
121.208 |
126.508 |
|
Année 5 |
105.637 |
113.428 |
125.641 |
131.147 |
|
Année 6 |
111.118 |
117.215 |
129.776 |
133.000 |
Tableau 3.8 : série chronologique 1
(période p = 4)
L’observation de chaque trimestre est soumis à un effet
particulier qui revient tous les ans ; il y a donc 4 variations saisonnières
correspondant chacune à un trimestre.
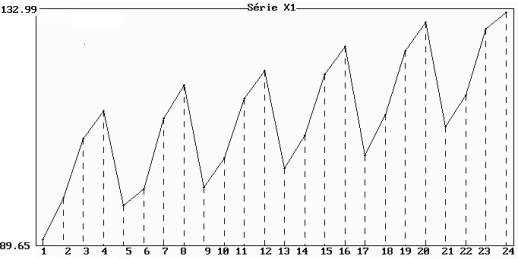
Figure 4.8 : représentation
graphique de la série 1
(données observées trimestriellement pendant 6 ans)
Définition : la période notée p des variations saisonnières est la longueur exprimée en unités de temps séparant deux variations saisonnières dues à un même phénomène.
Remarque : nous supposerons dans la suite que la série est soumise à des variations saisonnières de même période p. La période est alors le nombre de variations saisonnières. Cette hypothèse n’est pas toujours réalisée au départ : les ventes par tranches horaires d’un hypermarché sont soumises par exemple à une première variation saisonnière due à l’heure et à une seconde due à la journée. Ce cas est traité théoriquement en considérant une période égale au plus petit commun multiple des deux périodes : deux variations saisonnières de périodes 4 et 6 donnent une variation saisonnière de période 12 (= 3 x 4 = 2 x 6).
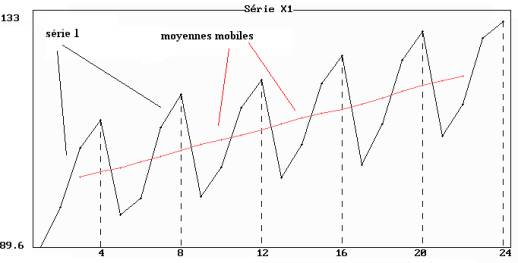
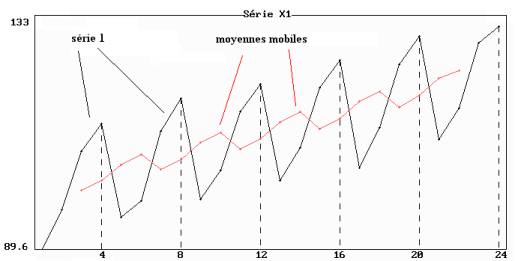
Il n'est pas toujours facile de distinguer la tendance lorsque la série chronologique est soumise à des variations saisonnières. La méthode mathématique consiste à calculer les moyennes mobiles en choisissant comme longueur la période des variations saisonnières, de façon à les faire disparaître. Si la moyenne mobile choisie est de longueur différente, les variations saisonnières ne sont pas toujours éliminées (cf. figures 5.8 et 6.8).
Ces moyennes mobiles ont en outre l'avantage d'atténuer les variations accidentelles comme nous l'avons vu précédemment, mais l'inconvénient de n'être définies ni au début ni à la fin de la période observée.
Exemple : on pourra comparer sur les
figures 5.8 et 6.8 ci-dessous les moyennes mobiles de longueur 4 (dont les
valeurs numériques sont données dans le tableau 4.8) et de longueur 5.
Figure 5.8 :
représentation simultanée de la série 1
et des moyennes
mobiles de longueur 4
Figure 6.8 : représentation simultanée de la série
1
et des moyennes mobiles de longueur 4
Contrairement aux m.m. de longueur 4, les m.m. de
longueur 5 n’éliminent pas les variations saisonnières.
Théorème : les moyennes mobiles d’une série soumise à des variations saisonnières de période p ne sont pas soumises à ces variations saisonnières si leur longueur l est égale à la période p, et plus généralement si leur longueur est un multiple de la période.
Ce théorème est démontré dans un complément pédagogique.
Conclusion : les moyennes mobiles d’une série chronologique dont la tendance est linéaire et les variations saisonnières sont de période p font apparaître la tendance et disparaître les variations saisonnières si leur longueur l est égale à la période p.
2. Modélisation et désaisonnalisation.
Un modèle de série chronologique est une équation précisant la façon dont les composantes s’articulent les unes par rapport aux autres pour constituer la série chronologique. Il existe de très nombreux modèles, et parmi eux deux modèles classiques simples : le modèle additif et le modèle multiplicatif, auxquels nous nous limiterons.
Dans les deux modèles présentés, la longueur des moyennes
mobiles doit être impérativement égale à la période des variations
saisonnières.
Nous avons présenté dans le tableau 3.8 les données sous une forme particulière : en lignes, ce sont les années, et en colonnes les trimestres : le terme xt correspondant à la te observation est alors noté xi,j, i donnant l'année (la ligne) et j le trimestre (la colonne).
La relation entre les indices i et j d’une part et l’instant t d’autre part est la suivante :
t = (i-1) p + j
Exemple :
|
|
j
= 1 |
j
= 2 |
j = 3 |
j = 4 |
|
i = 1 |
t
= 1 |
t
= 2 |
t
= 3 |
t
= 4 |
|
i
= 2 |
t
= 5 |
t
= 6 |
t
= 7 |
t
= 8 |
|
i
= 3 |
t
= 9 |
t
= 1° |
t
= 11 |
t
= 12 |
Exemple
pour n = 3 et p = 4
Nous utiliserons cette notation très souvent dans la suite du texte.
2.1 Modèle additif de série chronologique.
La série chronologique xt se décompose en une tendance notée ct, des variations saisonnières st de période p (égales à s1, s2, s3, …, sp) et d'une composante accidentelle et.
Le modèle le plus simple est le modèle additif, dans lequel la variation saisonnière s'ajoute simplement à la tendance :
|
pour tout t = 1, …, T |
xt = ct + st + et |
Le modèle additif s'exprime donc en général de la façon suivante :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j = ci,j + sj + ei,j |
Le terme sj caractérise la variation saisonnière à l’instant j de chaque période i : du trimestre j dans le cas particulier des séries 1 et 2 (p = 4), du mois j dans des données mensuelles (p = 12) etc.… Les moyennes mobiles seront aussi notées mmi,j.
Définition : les termes sj du modèle additif exprimé sous la forme précédente sont appelés coefficients saisonniers du modèle additif.
On peut calculer la différence entre l'observation et la tendance :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j – ci,j = sj + ei,j |
Pour un même trimestre, la différence entre l'observation et la tendance est donc à peu près constant et égale à sj (on suppose que la composante accidentelle est relativement faible).
Nous avons vu précédemment que les moyennes mobiles de longueur l égale à la période des variations saisonnières sont des approximations de la tendance. On peut donc considérer que la différence entre une observation xi,j et la moyenne mobile mmi,j correspondante est à peu près constante pour j fixé :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j
– mmi,j » sj |
Cette propriété est recherchée sur la représentation graphique de la série xt pour déterminer si cette série suit un modèle additif ou non. Elle peut être observée sur la figure 5.8 dans laquelle la tendance est caractérisée par les moyennes mobiles de longueur 4 : les différences entre x3 et mm3, entre x7 et mm7, entre x11 et c11 sont à peu près constantes, de même les différences entre x4 et mm4, x8 et mm8, x12 et mm12 etc.
On peut en déduire les différences xi,j – mmi,j. Les moyennes mobiles donnant une première approximation de la tendance ci,j, les colonnes du tableau des différences contiennent des approximations des coefficients sj.
Exemple : Les moyennes mobiles et
par suite différences xi,j – mmi,j ne sont pas définies
aux premier et deuxième trimestres de la première année, ni aux troisième et
quatrième trimestres de la dernière (tableaux 4.8 et 5.8).
|
|
1er trimestre |
2e trimestre |
3e trimestre |
4e trimestre |
|
Année 1 |
|
|
103.39678 |
104.44080 |
|
Année 2 |
105.14860 |
106.25917 |
107.31233 |
108.46116 |
|
Année3 |
109.65950 |
110.47448 |
111.27404 |
112.28937 |
|
Année 4 |
113.42748 |
114.58360 |
115.45379 |
116.22236 |
|
Année 5 |
117.24943 |
118.38337 |
119.64839 |
120.80691 |
|
Année 6 |
121.79719 |
122.54573 |
|
|
Tableau 4.8 : moyennes mobiles de longueur 4 de la série 1
|
1er trimestre |
2e trimestre |
3e trimestre |
4e trimestre |
|
|
Année 1 |
|
|
5.50932 |
9.71580 |
|
Année 2 |
-8.94393 |
-6.86050 |
5.45047 |
10.72334 |
|
Année3 |
-10.05746 |
-5.28258 |
5.28226 |
9.62153 |
|
Année 4 |
-10.15538 |
-4.93910 |
5.75471 |
10.28534 |
|
Année 5 |
-11.61263 |
-4.95497 |
5.99271 |
10.33979 |
|
Année 6 |
-10.67929 |
-5.33023 |
|
|
Tableau 5.8 : différences entre les observations et les
moyennes mobiles
de la série 1
Les
différences apparaissant dans une même colonne sont proches les uns des autres
et caractérisent le modèle additif.
Les différences xi,j – mmi,j sont donc des approximations des coefficients sj. Leur moyenne (ou leur médiane) , pour chaque colonne j, donne une première estimation sj':
|
|
|
1 |
n |
|
|
sj' |
= |
––– |
S |
(xi,j – mmi,j) |
|
|
|
n |
i = 1 |
|
On obtiendra enfin les estimations définitives sj en centrant ces termes sj’:
· on calcule la moyenne des sj’:
|
|
|
1 |
|
|
ms' |
= |
––– |
(s1' + s2' + … + sp') |
|
|
|
p |
|
· on centre en posant :
|
pour tout j =1, …, p |
sj = sj' – ms' |
Exemple : le tableau 5.8 donne les différences entre les observations et les moyennes mobiles. On en déduit les moyennes suivantes :
|
s1' = -10.2897 |
s2' = -5.4735 |
s3' = 5.5979 |
s4' = 10.1371 |
·
On calcule la moyenne des sj' : ms'
= -0.007039938
·
Les valeurs définitives sont obtenues en posant sj
= sj' – ms':
|
s1 = -10.2827 |
s2 = -5.4664 |
s3 = 5.6049 |
s4 = 10.1442 |
|
règle de
calcul des estimations des
coefficients saisonniers du modèle additif |
|
· on calcule les différences entre les observations et les moyennes mobiles ; |
|
· on calcule la moyenne ou la médiane sj’ des différences de chaque colonne du tableau ; |
|
· on calcule la moyenne ms' de ces valeurs sj' ; |
|
· on obtient les estimations sj en centrant les valeurs sj’ : sj = sj' – ms'. |
2.2 Modèle multiplicatif de série chronologique.
Le second modèle que nous étudions ici est le modèle multiplicatif suivant :
|
pour tout t = 1, …, T |
xt = ct (1 + st) + et |
En présentant les données comme dans le paragraphe précédent, le modèle multiplicatif s'exprime de la façon suivante :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j = ci,j ( 1 + sj ) + ei,j |
Le terme sj caractérise la variation saisonnière du trimestre j dans le cas particulier des séries 1 et 2, du mois j dans des données mensuelles etc.
On peut calculer la différence entre l'observation et la tendance :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j – ci,j = ci,j sj + ei,j |
Considérons le cas particulier j = 1 (1er trimestre de l’année i).
|
pour tout i = 1, …, n |
xi,1 – ci,1 = ci,1 s1 + ei,1 |
La différence xi,1 – ci,1 entre l'observation et la tendance est proportionnelle à la tendance ci,1 : lorsque cette tendance est croissante, la différence augmente, lorsqu'elle est décroissante, il diminue.
Le même raisonnement peut évidemment être tenu pour j fixé quelconque. Les différences permettent ainsi de déterminer si la série chronologique étudiée suit un modèle multiplicatif.
Exemple :
on considère la série chronologique ci-dessous :
|
|
1er
trimestre |
2e
trimestre |
3e
trimestre |
4e
trimestre |
|
Année 1 |
224.3705 |
253.2811 |
201.2421 |
248.9411 |
|
Année 2 |
274.3802 |
300.1641 |
248.9038 |
298.4386 |
|
Année 3 |
331.9657 |
371.4032 |
303.4313 |
365.9029 |
|
Année 4 |
406.6326 |
437.9967 |
361.5774 |
444.8447 |
|
Année 5 |
488.4166 |
536.5268 |
435.5698 |
549.3614 |
|
Année 6 |
598.0016 |
659.2896 |
533.2156 |
669.2675 |
Tableau 6.8 : série chronologique 2
(modèle multiplicatif , période p = 4)
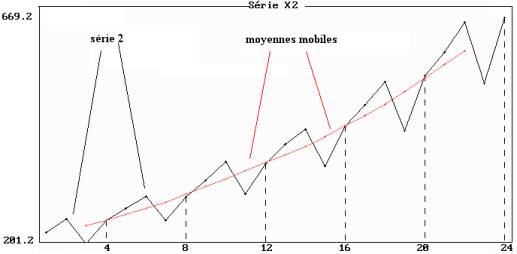
Figure 7.8 : série 2 et moyennes mobiles de longueur 4
Cette série est soumise à des variations saisonnières de
période 4 ; la tendance, caractérisée par les moyennes mobiles de longueur 4,
est croissante, et la différence entre une observation xt et la
moyenne mobile mmt a tendance à augmenter pour une même variation
saisonnière : l Les différences entre x3 et mm3,
entre x7 et mm7, entre x11 et c11
augmentent visiblement, de même que les différences entre x4 et mm4,
x8 et mm8, x12 et mm12 etc. (figure
7.8).
Pour quantifier les variations saisonnières, on considère les rapports xi,j / ci,j :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j / ci,j = 1 + sj + ei,j / ci,j |
En considérant que les variations accidentelles ei,j sont faibles par rapport à la tendance ci,j et en utilisant l'approximation de la tendance par les moyennes mobiles, on constate donc que les rapports x3 / mm3, x7 / mm7, x11/mm11, … sont à peu près constants et donnent une approximation de 1 + s3, de même les rapports x4 / mm4, x8 / mm8, x12 / mm12 etc. donnent une approximation de 1 + s4 :
|
|
xi,j |
|
|
|
pour tout j = 1, …, p |
–––––– |
= |
1 + sj = S j |
|
|
mmi,j |
|
|
Exemple :
les tableaux 7.8 et 8.8 ci-dessous contiennent les moyennes mobiles de la série
et les rapports xi, j / mmi,j.
|
1er
trimestre |
2e
trimestre |
3e
trimestre |
4e
trimestre |
|
|
Année 1 |
|
|
238.210 |
250.322 |
|
Année 2 |
262.140 |
274.284 |
287.670 |
303.773 |
|
Année3 |
319.494 |
334.743 |
352.509 |
370.167 |
|
Année 4 |
385.759 |
402.895 |
422.986 |
445.525 |
|
Année 5 |
467.090 |
489.404 |
516.167 |
545.210 |
|
Année 6 |
572.761 |
599.955 |
|
|
Tableau 7.8 : moyennes mobiles de longueur 4 de la série 2
|
|
1er trimestre |
2e
trimestre |
3e
trimestre |
4e
trimestre |
|
Année 1 |
|
|
0.84481 |
0.99449 |
|
Année 2 |
1.04670 |
1.09435 |
0.86524 |
0.98244 |
|
Année3 |
1.03904 |
1.10952 |
0.86078 |
0.98848 |
|
Année 4 |
1.05411 |
1.08712 |
0.85482 |
0.99847 |
|
Année 5 |
1.04566 |
1.09629 |
0.84385 |
1.00761 |
|
Année 6 |
1.04407 |
1.09890 |
|
|
Tableau 8.8 : rapports des observations aux moyennes mobiles de la série 2
Les rapports dans chaque colonne du tableau 8.8 sont à
peu près constants.
Les rapports xi,j / mmi,j sont donc des approximations des termes 1 + sj que l'on appelle coefficients saisonniers dans le cas du modèle multiplicatif.
Définition : les termes Sj = 1 + sj du modèle multiplicatif exprimé sous la forme précédente sont appelés coefficients saisonniers du modèle multiplicatif.
On obtient des premières estimations Sj' des coefficients saisonniers en calculant la moyenne (ou la médiane) des rapports figurant dans chaque colonne. Par analogie avec les coefficients saisonniers sj du modèle additif, dont la moyenne est égale à 0, on cherche des estimations définitives Sj de moyenne 1 :
· on calcule la moyenne :
|
|
|
1 |
|
|
mS' |
= |
––– |
(S1'
+ S2' + … + Sp') |
|
|
|
p |
|
·
on
pose :
|
pour tout j =1, …, p |
Sj = Sj' /
mS' |
Les coefficients saisonniers estimés Sj sont ainsi de somme p :
|
|
|
1 |
|
|
S1 + S2 + … + Sp |
= |
––– |
( S1’ + S2’ + … + Sp’ ) |
|
|
|
mS’ |
|
|
|
= |
p |
|
ce qui équivaut à une moyenne des sj égale à 0 puisque l'on a Sj = 1 + sj.
Exemple :
· le tableau 8.8 donne les rapports des observations aux moyennes mobiles.
·
on en déduit les moyennes suivantes :
|
S1' = 1.045913 |
S2' = 1.097236 |
S3' = 0.8539006 |
S4' = 0.9942986 |
·
on calcule la moyennes des Sj' : mS'
= .9978371
·
les valeurs définitives sont obtenues de façon que
les Sj' soient de moyenne 1 :
|
S1 = 1.04818 |
S2 = 1.099614 |
S3 = 0.8557515 |
S4 = 0.9964539 |
|
règle de calcul des estimations des coefficients
saisonniers du modèle multiplicatif |
|
· on calcule les rapports des observations aux moyennes mobiles ; |
|
· on calcule la moyenne ou la médiane des rapports Sj’ de chaque colonne du tableau ; |
|
· on calcule la moyenne mS’ de ces valeurs ; |
|
· on obtient les estimations Sj en posant Sj=Sj’ / mS’. |
2.3 Désaisonnalisation.
Les coefficients saisonniers permettent d'éliminer d'une observation les effets de la variation saisonnière correspondante. On obtient ainsi les valeurs corrigées des variations saisonnières, ou encore les valeurs désaisonnalisées.
L'avantage de cette désaisonnalisation est de permettre la comparaison de deux observations soumises à des variations saisonnières différentes.
définition : on appelle observation corrigée des variations saisonnières la valeur xi,j' obtenue en éliminant l'effet saisonnier sur la valeur xi,j.
|
modèle additif : |
xi,j' = xi,j – sj |
|
modèle multiplicatif : |
xi,j' = xi,j / Sj |
Les valeurs corrigées des variations saisonnières (expression souvent abrégée par c.v.s.) caractérisent à la fois la tendance et la variation accidentelle.
Exemple : on donne ci-dessous les quatre dernières observations de la série 2 (année 6) et les valeurs corrigées des variations saisonnières :
|
|
1er trimestre |
2e trimestre |
3e trimestre |
4e trimestre |
|
observations : |
598.00160 |
659.28960 |
533.21560 |
669.26750 |
|
valeur c.v.s. : |
570.51396 |
599.56452 |
623.09629 |
671.64924 |
L'observation du deuxième trimestre est largement supérieure à celle du troisième, mais c'est l'inverse pour les valeurs c.v.s. : la tendance est restée croissante au troisième trimestre.
Supposons que l'observation du premier trimestre de l'année 7 soit égale à 720.15. Pour savoir si la tendance est restée à la hausse, on calcule la valeur désaisonnalisée :
x7,1' = 720.15/1.04818 = 687.04771
et on la compare à la valeur désaisonnalisée du quatrième trimestre de l'année précédente :
x6,4' = 671.649
La valeur c.v.s. x7,1' est supérieur à x6,4'. La tendance est restée à la hausse si la différence est supérieure à la variation accidentelle . Il faudrait donc comparer cette différence à l’écart type des variations accidentelles, calculé sur les données antérieures. Il semble que dans la pratique, cette comparaison ne soit guère effectuée.
3. Filtre de Buys-Ballot.
Le filtre de Buys-Ballot concerne les séries chronologiques suivant un modèle additif et dont la tendance est linéaire. Il consiste à estimer les paramètres de ce modèle suivant le critère des moindres carrés, et permet ensuite, dans la mesure où les hypothèses sont respectées, d'effectuer des prévisions. Il s’agit en fait d’une régression linéaire multiple particulière.
Lorsque la série suit le modèle multiplicatif et que la tendance est exponentielle, les logarithmes des observations vérifient les conditions précédentes. On peut alors appliquer le filtre de Buys-Ballot.
3.1 Filtre de Buys-Ballot.
Nous supposons donc que la série étudiée suit le modèle additif et que la tendance est linéaire :
ct = b t + a
Pour exprimer la tendance en fonction de la ligne i et de la colonne j du tableau, nous utilsons la relation et les variables t, i et j données précédemment :
t = (i-1) p + j
dans laquelle i varie de 1 à n, j de 1 à p. Le nombre total T d'observations est égal à n p.
Le modèle complet est le suivant :
|
pour tout i = 1, …, n |
pour tout j = 1, …, p |
xi,j = b [(i-1) p + j ] + a + sj + ei,j |
Les coefficients en caractères grecs sont des coefficients théoriques qu’il s’agit d’estimer : on retrouve ici la notation employée dans le chapitre précédent. Les observations de la variable expliquée sont notées ici xi,j, et les variables explicatives sont le temps t et p variables particulières qui n’apparaissent pas directement dans la formule et dont les coefficients de régression sont les variations saisonnières sj.
Le critère des moindres carrés consiste à déterminer les paramètres b, a, s1, s2, …, sp de façon à minimiser la somme des carrés des différences ei,j = xi,j – [( b (i-1) p + j + a + sj ] entre la valeur observée xi,j et la valeur estimée par le modèle b [(i-1) p + j ] + a + sj.
Les valeurs obtenues sont des estimations des paramètres théoriques b, a, sj. Le coefficient de corrélation du modèle est le coefficient de corrélation entre les valeurs observées xi,j et les valeurs estimées xi,j’.
On calculera les estimations des paramètres à l’aide des formules suivantes :
|
a |
= |
m – b ( n p + 1)/2 |
|||
|
sj |
= |
m.j – m – b [ j – ( p + 1 )/2 ] |
|
|||
avec les notations suivantes :
m : moyenne de la totalité des observations
mi. : moyenne des observations de la ligne i
m.j : moyenne des observations de la colonne j
définition : les termes ei,j = xi,j – [ [ b (i-1) p + j ] + a + sj ] sont appelés résidus.
Comme en régression, la variance des résidus s2 dépend du coefficient de corrélation r et de la variance sx2 des observations xi,j de la variable expliquée :
|
s2 = sx2 ( 1 – r2) |
L’interprétation du coefficient de corrélation est délicate dans le cas des séries chronologiques. Il est souvent très élevé (une valeur de 0.98 n’est pas rare) sans que l’on puisse en déduire directement que l’ajustement obtenu est satisfaisant. Cette particularité est due au fait que la variable temps est ordonnée. Dès lors, il suffit que la tendance soit croissante ou décroissante pour que le coefficient de corrélation soit élevée. Mais il ne donne aucun renseignement sur la nature de la tendance, qui peut être exponentielle ou linéaire etc.
Exemple : le modèle additif et l'hypothèse de linéarité de la tendance de la série 1 sont confirmés par la représentation graphique (figure 8.8).
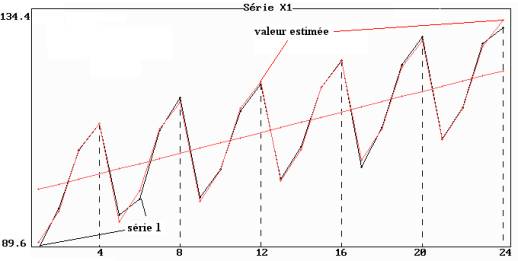
Figure 8.8 : représentation simultanée de la série 1,
de la tendance
et des
valeurs estimées par le modèle
Nous donnons les résultats partiels suivants :
|
années |
moyennes annuelles mi. |
produits i mi. |
|
1 |
102.57846 |
102.57846 |
|
2 |
106.88766 |
213.77531 |
|
3 |
110.81528 |
332.44585 |
|
4 |
115.15820 |
460.63280 |
|
5 |
118.96325 |
594.81625 |
|
6 |
122.77737 |
736.66425 |
On en
déduit le modèle estimé par le filtre de Buys-Ballot :
|
b =
1.011173 |
a = 100.2237 |
|
s1
= -10.43134 |
s2 = -5.27912 |
|
s3 = 5.77288 |
s4 = 9.93759 |
|
r = 0.99791 |
s² = 0.5641465 |
Tableau 9.8 : paramètres du modèle linéaire additif
estimés par le filtre de Buys-Ballot sur la série 1
L'ajustement peut être considéré comme très précis puisque le coefficient de corrélation entre les observations xi,j et les estimations xi,j' est égal à 0.99791.
La série 1 n'est pas une série réelle : elle a été obtenue par simulation du modèle linéaire additif avec comme paramètres théoriques :
xt = b t + a + st + et
b = 1, a = 100, et » N(0,1), s1 = -10, s2 = -5, s3 = 5, s4 = 10.
Les valeurs estimées sont visiblement très proches des valeurs théoriques. La méthode statistique permet donc de retrouver à partir des observations les valeurs des paramètres utilisés pour générer les données. C’est le moins qu’on pouvait en attendre.
3.2 Validation du modèle linéaire et prévision.
Pour effectuer la prévision xi,jp de la série chronologique à l’instant t = (i-1) p + j, on remplace dans le modèle théorique les paramètres par leurs estimations :
|
xi,jp = b [(i-1) p + j ] + a + sj |
Ces prévisions ponctuelles peuvent être complétées par des prévisions par intervalle de confiance, comme en régression, mais nous ne donnerons pas les formules trop complexes pour être utilisées facilement.
Exemple :
Les valeurs estimées par le modèle sont données par la formule :
|
xi,j = 1.011173 [ (i-1)
4 + j ] + 100.2237 + sj |
avec :
|
s1 = -10.43134 |
s2 = -5.27912 |
s3 = 5.77288 |
s4 = 9.93759 |
Les prévisions concernant l'année 7 sont les suivantes :
|
x7,1p = 115.07169 |
x7,2p = 121.23509 |
x7,3p = 133.29826 |
x7,4p = 138.47414 |
Les prévisions que l'on peut effectuer après l'estimation des paramètres ne sont justifiées que dans la mesure où les hypothèses du modèles sont respectées.
Une hypothèse fondamentale pour la prévision et souvent négligée est que les conditions dans lesquelles la série chronologique évolue sont les mêmes à la date de la prévision que dans le passé. Il faut noter que cette condition n’est pas toujours vérifiée, par l’effet de la prévision elle-même : par exemple, un hypermarché qui prévoit une baisse de son chiffre d’affaires va prendre des mesures de réduction de coût, augmenter sa publicité etc., de façon à augmenter ses ventes : les décisions vont donc à l’encontre de la prévision.
Il est indispensable en outre de contrôler statistiquement le modèle. Pour cela, on étudie les résidus ei,j. Ces résidus possèdent les propriétés mathématiques habituelles en régression : ils sont centrés, indépendants de la variable explicative (ici le temps). Les résidus de chaque trimestre sont en outre de moyenne nulle.
Pour que le modèle soit valide, leur répartition doit être proche de la loi normale. Ils ne doivent présenter pas d'évolution particulière dans le temps, ce que l’on peut vérifier par une représentation graphique ou par des tests (tests de Durbin et Watson, sur le coefficient d’autocorrélation de rang 1).
Rappelons enfin que la prévision xi,jp est la prévision de la moyenne des observations pour t fixé : l’intervalle de confiance donné par certains logiciels est celui de cette moyenne, et non de la valeur individuelle à l’instant t.
4. Lissage exponentiel.
4.1 Généralités sur le lissage exponentiel.
Le lissage exponentiel est une classe de méthodes de lissage de séries chronologiques dont l'objectif est la prévision à court terme. Ces méthodes sont fondées sur une hypothèse fondamentale : chaque observation à l’instant t dépend des observations précédentes et d'une variation accidentelle, et cette dépendance est plus ou moins stable dans le temps.
L'estimation xtp de la série à l’instant t connaissant xt-1 est donc obtenue par une formule de la forme :
xtp = at-1 x0 + at-2x1 + at-3 x2 + …. + a0 xt-1
On peut généraliser cette formule au cas où seule l'observation xt-h est connue :
xtp = at-h x0 + at-h-1 x1 + at-h-2 x2 + …. + a0 xt-h
Dans le premier cas, on peut prévoir à l’horizon 1 : sachant xt, on prévoit xt+1, l'observation suivante, et dans le cas général, on peut prévoir à l'horizon h : sachant xt, on prévoit xt+h. On peut penser que plus l'horizon h est faible, meilleure est la prévision.
Les méthodes de lissage exponentiel consistent à choisir les coefficients aj en fonction de la série étudiée.
· Dans le cas où la série est stationnaire (on ne distingue pas de tendance à la hausse ni à la baisse), on utilise le lissage exponentiel simple. Les coefficients aj sont de la forme :
aj = aj / (1 – a)
où a est la constante de lissage choisie de façon empirique entre 0 et 1. La valeur 1/a est parfois appelée âge moyen du lissage.
· Lorsque la série présente une tendance linéaire par morceaux (la tendance peut être considérée comme linéaire sur une suite de quelques observations), et n'est soumise à aucune variation saisonnière, on effectue les prévisions à l'aide du double lissage exponentiel. En effet, en appliquant deux fois le lissage exponentiel simple, on détermine une suite de droites de tendance qui ajustent les observations.
· Dans le cas d’une série soumise à des variations saisonnières, on utilise souvent le modèle de Holt et Winters, que nous expliquons rapidement dans le paragraphe 4.2.
Dans les lissages exponentiels simple et double, il y a donc une seule constante à fixer. Le choix peut être empirique, c’est-à-dire effectué par l’utilisateur en fonction de la connaissance qu’il a de la série. Lorsque la valeur xt ne dépend guère que des 3 ou 4 dernières observations, on peut choisir la constante a proche de 1. Inversement, si les observations antérieures gardent longtemps une influence sur la valeur xt, on choisira a proche de 0. On peut aussi déterminer la constante de façon à minimiser la somme des carrés des erreurs commises pour l’horizon h fixé. Certains programmes proposent cette option.
Exemple : la figure 9.8
ci-dessous montre l'ajustement obtenu à l'horizon 1 du cours de l’action
Alcatel par un double lissage exponentiel.
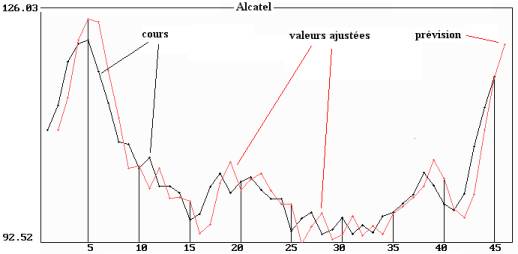
Figure 9.8 : cours du titre Alcatel et prévision à
l’horizon 1
par double lissage exponentiel (a = 0.65)
La constante de lissage a été déterminée
de façon à minimiser la somme des carrés des erreurs (a = 0.65). La valeur prévue
suit la série avec retard.
Le
cours prévu à l’instant t = 46 (8 mars 1999) est égal à 122.22 € ; le cours
moyen observé de la séance est de 118 € : la prévision n’est pas très
satisfaisante. Les méthodes de prévision ne donnent pas de bons résultats sur
les cours en Bourse (sinon, cela se saurait !).
4.2 Modèle de Holt et Winters.
La méthode de Holt et Winters permet en effet d'effectuer des prévisions sur des séries chronologiques assez irrégulières et soumises ou non à des variations saisonnières suivant un modèle additif ou multiplicatif.
Elle consiste en trois lissages exponentiels simultanés. On définit donc trois paramètres, notés a, b et g. A chaque instant t, elle donne une estimation :
· de la tendance
· du coefficient saisonnier correspondant
· de la valeur observée.
On peut choisir les coefficients arbitrairement : faibles si l'on considère que la valeur à l’instant t dépend d'un grand nombre d'observations antérieures, élevés dans le cas contraire. On peut aussi en calculer les valeurs optimales, en minimisant la somme des carrés des différences entre les valeurs observées et estimées. On procède ensuite aux prévisions, en considérant que la tendance suit un modèle linéaire additif ou multiplicatif à très court terme.
Exemple
: on étudie ici la série constituée du nombre trimestriel de
naissances dans la région Centre. La figure 10.8 montre une tendance assez
irrégulière, avec des variations saisonnières de période 4.
Le filtre de Buys-Ballot n'est visiblement pas adapté dans
ce cas particulier, et nous appliquons ici le modèle de Holt et Winters. Nous
choisissons comme modèle un modèle dont la tendance à court terme est linéaire
(ici, on se limite à examiner une succession de quelques points), et les variations
de période 4 additives. Nous fixons l'horizon à 4 pour disposer des prévisions
de toute l'année 1986.
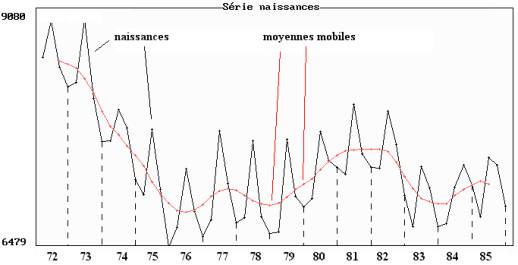
Figure 10.8 : nombre de naissances dans la région Centre de 1972 à 1985
Moyennes mobiles de longueur 4.
Les paramètres optimaux que l'on obtient en minimisant la
somme des carrés de la totalité des résidus sont : a =
0.9, b
= 0.9, g
= 0.1.
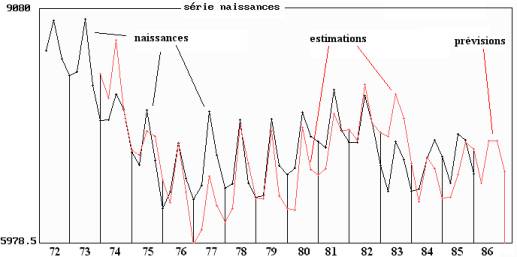
Figure 11.8 : nombre de naissances dans la région
Centre de 1972 à 1985
Estimations par le modèle de Holt et Winters et prévision
pour 1986
Le tableau 10.8 permet de comparer prévisions et observations de l'année 1986 : les naissances aux deux premiers trimestres ne sont pas très bien estimées, contrairement aux deux dernières.
|
1er trimestre |
2e
trimestre |
3e
trimestre |
4e trimestre |
|
|
observations |
7018 |
7720 |
7415 |
6986 |
|
prévisions |
6824 |
7410 |
7405 |
6984 |
Tableau 10.8 : nombre de naissances dans la région Centre observés et prévus en 1986
Conclusion
L'analyse des séries chronologiques est un des objectifs fondamentaux de la statistique. Nous insistons sur le fait, que quelle que soit la méthode utilisée, il faut être vigilant sur les prévisions effectuées qui peuvent être dans certains cas totalement aberrantes (cf. Bensaber et Bleuse-Trillon, p. 123, à propos du modèle de Holt et Winters).
Nous conseillons fortement aux praticiens de se limiter aux méthodes qu’ils connaissent lorsqu’ils effectuent leurs prévisions. Le logiciel qu’ils utilisent doit être sûr, contrôlé : il nous est arrivé d’obtenir des résultats différents sur les mêmes données et par la même méthode en employant deux logiciels différents, ou d’aboutir des prévisions manifestement fausses puisque différentes des valeurs données dans les ouvrages de référence.
TABLE DES MATIERES
1. Description d'une série
chronologique.
1.1 Description de la tendance.
1.2 Description simultanée des
variations saisonnières et de la tendance.
2.
Modélisation et désaisonnalisation.
2.1 Modèle additif de série
chronologique.
2.2 Modèle multiplicatif de série
chronologique.
3.2 Validation du modèle linéaire et
prévision.
4.1 Généralités sur le lissage
exponentiel.
4.2 Modèle de Holt et Winters.