échelle Logarithmique

L’échelle logarithmique, fréquemment utilisée pour représenter des indices, variables ou grandeurs économiques, est fondée sur les propriétés de la fonction logarithme décimale notée log , et définie par la fonction réciproque de la fonction exponentielle 10^x:

y = 10 ^x

Û

x = log y

On sait que 10⁰ = 1. Donc :

· quand x varie entre 0 et 1, y varie entre 1=10⁰ et 10 =10¹; pour x = 1/2, on a y = 10^1/2 = 3.1623

· quand x varie entre 1 et 2, y varie entre 10 et 10² ; pour x = 3/2, on a y = 10^3/2 = 10 x 10^1/2 = 31.623

· quand x varie entre 2 et 3, y varie entre 10² et 10³ ; pour x = 5/2, on a y = 10² x 10^1/2 = 316.23

· pour y = 5, on a x = log y = 0.699 (10^0.699 = 5)

· pour y = 50, on a x = log y = 1.6990 (10^1.6990 = 50)

· pour y = 500, on a x = log y = 2.6990 (10^2.3979 = 500)

L’échelle logarithmique sur l’axe des ordonnées revient à représenter les valeurs log(y_i) au lieu de y_i. Cela revient à graduer l’axe des ordonnées par les puissances de 10.

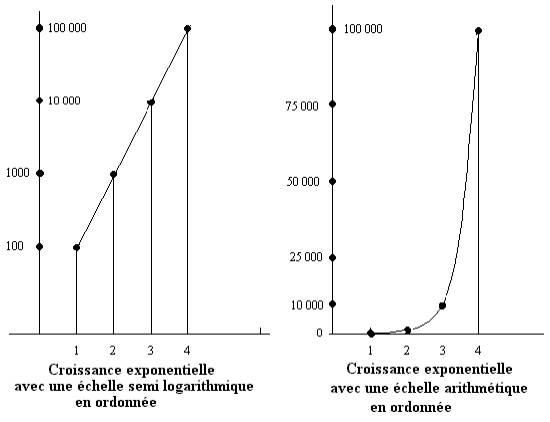
Par exemple, l’axe des ordonnées ci-dessous est gradué de la façon suivante : le premier centimètre représente 1 à 10, le deuxième 10 à 10² = 100, le troisième 10² à 10³ = 1000, etc...  L’avantage est de rendre possible la représentation graphique d’une grandeur économique qui augmente très vite comme on peut le voir sur les figures ci-dessous.

On peut effectuer les représentations graphiques sur du papier spécial, appelé papier semi-logarithmique, sur lequel l’échelle est directement représentée.