régression polynômiale

à la bourse de paris

Nous reprenons une étude de cas proposée par A. Bensaber et B. Bleuse-Trillon (cf. bibliographie) qui ont analysé l’évolution de l’indice INSEE des valeurs françaises à la Bourse de Paris de 1962 à 1986. Les données et les paramètres figurent dans les fichiers bourse.dat et bourse.par.

Nous expliquons ici la hausse des valeurs boursières en fonction du temps :

y_t = f(t) + e

La figure 1 ci-dessous montre une évolution non linéaire de l’indice boursier, avec une croissance très rapide de 1982 à 1986 :

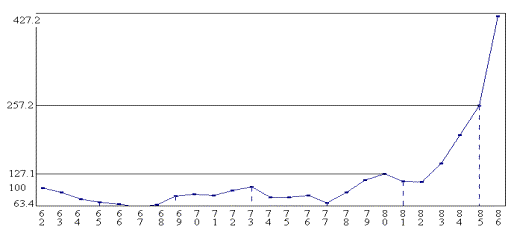
Figure1 : Indice INSEE des valeurs françaises

à la Bourse de Paris de 1962 à 1986

Nous nous limitons à l’étude des 21 dernières observations, de 1966 à 1986, pour pouvoir utiliser les résultats de cette analyse dans l’étude de cas « L’inflation boursière ».

On peut envisager un ajustement exponentiel ou polynômial pour caractériser la tendance de cette série. L’ajustement exponentiel consiste à effectuer une régression linéaire sur la série des logarithmes :

ln y_t = b₀ + b₁ t + e_t

La série des logarithmes et les paramètres des données se trouvent dans les fichiers bourse2.dat et bourse2.par, et les calculs ont été effectués par le programme d’analyse d’une série chronologique de StatPC.

Le modèle estimé est le suivant :

ln y_t » 3.994804 + 0.0618002 t

Le coefficient de corrélation linéaire est égal à 0.81703 et la variance estimée des résidus à 0.0771.

La figure 2 montre que l’ajustement linéaire des logarithmes n’est pas satisfaisant. Elle suggère plutôt un ajustement linéaire en deux morceaux, le premier de 1966 à 1977, le second de 1978 à 1986. On peut envisager aussi un nouvel ajustement exponentiel.

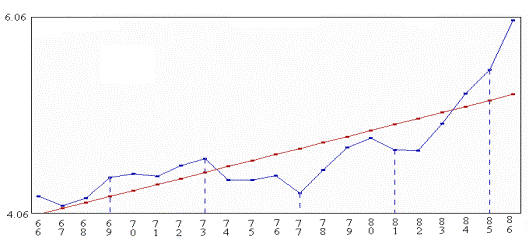
Figure 2 : logarithme de l’indice INSEE des valeurs françaises

à la Bourse de Paris de 1962 à 1986

Les résidus, dont le coefficient de corrélation avec la variable explicative, ici l’année, est nul, présentent une tendance évidente à la hausse à la fin de la période. L’ajustement exponentiel effectué ne correspond donc pas à la nature des données.

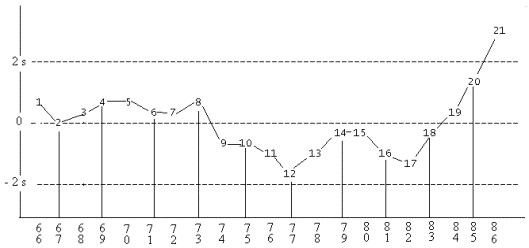
Figure 3 : résidus obtenus par l’ajustement exponentiel

de l’indice INSEE des valeurs françaises

à la Bourse de Paris de 1962 à 1986.

A. Bensaber et B. Bleuse-Trillon proposent d’effectuer un ajustement polynômial, qui consiste à introduire dans le modèle de régression des fonctions puissances de la variable explicative, ici le temps. Le modèle est donc le suivant :

y_t = b₀ + b₁ t + b₂ t² + …+ b_p t^p + e_t

Il s’agit donc d’une régression linéaire multiple.

Suivant le principe de parcimonie, le nombre de variables explicatives doit être le plus petit possible : on peut en proposer ici une explication par le fait que, en considérant p = 20, on obtiendrait un ajustement exact des 21 points de la même façon que par deux points il passe une droite, par trois points un polynôme de degré 2 etc. Ces relations purement numériques n’ont évidemment pas de sens au plan statistique.

Nous allons donc nous limiter à p = 4. Pour simplifier les calculs, nous définissons l’origine des temps par t = 5. Les résultats numériques ci-dessous, calculés en double précision, sont légèrement différents de ceux de Bensaber et Bleuse-Trillon.

On obtient le modèle ci-dessous :

y_t » -116.3697 t + 16.7282 t² - 0.9610 t³ + 0.0192 t⁴ +345.905

Les tests de Student montre que tous les coefficients sont significatifs :

coefficient	estimation	test de Student
b1	-116.3697	-2.203
b2	16.7282	2.771
b3	- 0.9610	-3.378
b4	0.0192	4.075

Le rapport de corrélation est hautement significatif : R² = 0.9573, et les résidus ne montrent pas de tendance particulière :

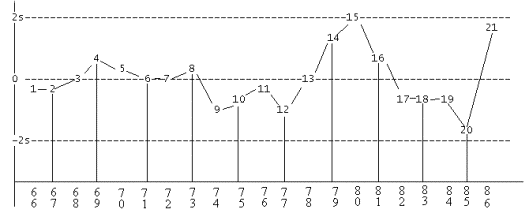
Figure 3 : résidus obtenus par l’ajustement polynomial

de l’indice INSEE des valeurs françaises

à la Bourse de Paris de 1962 à 1986.

La répartition des résidus est plus difficile à étudier. Le petit nombre de valeurs empêche de contrôler si leur répartition est gaussienne par un test d’ajustement du c², mais le test de Kolmogorov est positif et permet d’accepter cette hypothèse :

Probabilité critique ou p-value : PC =P(D > 0.1027) = 0.9797

En conclusion, l’ajustement est statistiquement satisfaisant, la dernière valeur observée (n°21) créant toutefois quelques difficultés dont nous parlons dans l’étude de cas plus complète : Inflation à la Bourse de Paris.

Son intérêt se limite à un lissage de la série. Il n’est pas envisageable d’effectuer des prévisions suivant ce modèle, que rien ne permet de supposer valide pour les années qui suivent. Le choix du temps comme variable explicative est discutable, et on ne voit pas comment il pourrait intervenir directement dans l’évolution de la Bourse. D’ailleurs, le krach boursier de 1987 nous rappelle à la prudence dans ce domaine.

Notons pour finir que nous n’avons pas effectué les démarches plus spécialement adaptées à l’étude de données chronologiques : lissage de la série par les moyennes mobiles, test sur les coefficients d’autocorrélation (voir l’étude de cas sur les processus autorégressifs), tests de Durbin et Watson (voir l’ouvrage de Bensaber Bleuse-Trillon) etc…