régression linéaire multiple
sur composantes principales
Cette étude de cas utilise des données simulées pour mettre en évidence l’intérêt et les difficultés de la régression sur composantes principales. Tous les traitements statistiques ont été effectués avec StatPC.
On considère un ensemble d’étudiants dont on connaît les notes moyennes annuelles dans cinq disciplines : la gestion, les mathématiques, la langue étrangère, l’expression et l’économie. L’objectif de l’analyse est d’analyser les relations entre les cinq variables pour reconstruire la note d’économie à l’aide des autres. Pour cela, on effectue la régression linéaire multiple. Le problème posé est de déterminer le meilleur ensemble de variables explicatives possible.
procédures de simulation
On dispose d’un échantillon de taille 10 dont les paramètres sont définis par le fichier exreg.par. En simulant cet échantillon par l’option prévue dans le menu principal de la régression linéaire multiple, on crée un échantillon de taille 100 de loi multinormale de mêmes paramètres théoriques (mêmes moyennes, variances et corrélations) que le premier. On effectue ensuite dans cet échantillon un tirage aléatoire sans remise donnant :
· un premier échantillon de taille 50, utilisé pour effectuer les calculs (dsreg0.par, dsreg0.dat).
· un second échantillon de taille 50 pour contrôler les résultats des modèles sélectionnés (dsreg1.par, dsreg1.dat).
Procédures de calcul.
Régression linéaire multiple (quatre variables explicatives).
On effectue la régression linéaire multiple en considérant l’ensemble des variables explicatives. On en déduit les estimations des coefficients de régression :
COEFFICIENTS DE REGRESSION
|
Variable |
coefficient de régression |
écart-type |
t de Student |
|
Gestion |
0.8005 |
0.1415 |
5.658 |
|
Maths. |
-0.0835 |
0.1200 |
-0.696 |
|
Langue |
-0.4033 |
0.1552 |
-2.598 |
|
Expression |
0.1792 |
0.1118 |
1.603 |
|
Constante |
5.6493 |
0.9232 |
6.119 |
ANALYSE DE VARIANCE
|
|
ddl |
Somme des carrés |
variance estimée |
% de variance totale |
|
Totale |
49 |
268.9013 |
5.4878 |
1 |
|
Expliquée |
4 |
206.9611 |
4.1113 |
0.7697 |
|
Résiduelle |
45 |
61.9402 |
1.3764 |
0.2303 |
|
R = 0.8773 |
P[F(4,45) > 37.590] =0 |
|
Somme des carrés des rés. 61.9402 |
Variance résiduelle estimée 1.37645 |
Régression linaire multiple ( deux variables explicatives).
Les procédures ascendantes et descendantes de sélection des variables explicatives ont donné le même résultat, pour des risques égaux à 10% : les variables explicatives introduites dans le modèle sont la note de gestion et la note de langue. Les résultats sur le fichier de calcul sont les suivants :
COEFFICIENTS DE REGRESSION
|
Variable |
coefficient de régression |
écart-type |
t de Student |
|
Gestion |
0.7094 |
0.0648 |
10.942 |
|
Langue |
-0.2123 |
0.0909 |
-2.335 |
|
Constante |
5.7231 |
0.8504 |
6.730 |
ANALYSE DE VARIANCE
|
|
ddl |
Somme des carrés |
variance estimée |
% de variance totale |
|
Totale |
49 |
268.9013 |
5.487781 |
1 |
|
Expliquée |
2 |
203.4217 |
4.094598 |
0.756492 |
|
Résiduelle |
47 |
65.47962 |
1.393183 |
0.243508 |
|
R =0.8698 |
P [F(2,47)> 73.006] = 0.0000 |
|
Somme des carrés des rés. 65.4796 |
Variance résiduelle estimée 1.39318 |
Régression sur composantes principales :
On effectue l’analyse en composantes principales des quatre variables explicatives potentielles. On sélectionne ensuite parmi les composantes principales celles dont le coefficient de corrélation avec la variable expliquée est significativement non nul pour un risque égal à 10%.
REGRESSION SUR LES COMPOSANTES PRINCIPALES
|
Composante principale |
Valeur propre |
Corrélation avec Y |
F observé |
ddl |
prob. crit. |
|
C1 |
2.698 |
0.714 |
51.023 |
1,49 |
0.0000 |
|
C2 |
0.948 |
-0.439 |
11.466 |
1,48 |
0.0000 |
|
C3 |
0.291 |
0.045 |
0.096 |
1,47 |
0.7559 |
|
C4 |
0.063 |
0.254 |
3.251 |
1,47 |
0.0743 |
Le risque de première espèce est fixé comme auparavant à 10%. On sélectionne donc les composantes principales C1, C2 et C4. Cette sélection est d’ailleurs celle qui minimise la statistique de Mallows Cq – q utilisée pour sélectionner un système de prédicteurs en vue d’effectuer des prévisions.
On note que la valeur propre l4 est faible (l4 = 0.063), et que cela induit vraisemblablement une colinéarité entre les variables, c’est-à-dire une augmentation des variances des estimateurs des coefficients de régression. Cette petite valeur propre permet par ailleurs d’interpréter la composante principale correspondante comme un bruit blanc, c’est-à-dire caractérisant des variations purement aléatoires. On décide donc d’éliminer cette composante principale.
COEFFICIENTS DE REGRESSION SUR LES VARIABLES INITIALES
APRES SELECTION DES COMPOSANTES PRINCIPALES C1, C2
|
Variable |
coefficient de régression |
écart-type |
t de Student |
|
Gestion |
0.3006 |
0.0303 |
9.938 |
|
Maths. |
0.3297 |
0.0369 |
8.949 |
|
Langue |
0.0024 |
0.0468 |
0.051 |
|
Expression |
-0.0305 |
0.0438 |
-0.697 |
|
Constante |
4.5748 |
|
|
|
R = 0.8384 |
P[F(2,47) > 55.60] = 0.0000 |
|
Somme des carrés des rés. 79.885 |
Variance résiduelle estimée 1.7000 |
Procédures de test
Le logiciel StatPC permet de conserver sur fichiers implicites les estimations des coefficients de régression, dans l’ordre où ils sont calculés. On peut donc effectuer les prévisions de la variable expliquée suivant chaque modèle. Ces prévisions, sur le fichier de calcul dsreg0.dat, aboutissent aux résultats obtenus par les méthode de régression correspondantes (mêmes résidus). Par contre, lorsque ces modèles sont appliqués aux données figurant sur le fichier test, les résidus les plus petits au sens de la moyenne de leurs carrés indiquent le modèle le meilleur. Le critère choisi est ici la moyenne des carrés des résidus et non leur variance, puisque leur moyenne n’est pas nécessairement égale à 0.
Le coefficient de corrélation multiple R indiqué dans le tableau ci-dessous est le coefficient de corrélation linéaire entre la note d’économie observée et la note d’économie estimée par le modèle sur les données tests.
|
|
Gestion, maths., langue, expression |
Gestion et langue |
C1 et C2 |
|
moyenne des résidus |
-0.129 |
-0.176 |
0.006 |
|
moyenne des carrés |
1.419 |
1.541 |
0.857 |
|
R |
0.719 |
0.692 |
0.820 |
Tous ces résultats montrent de façon évidente que le meilleur modèle de régression est défini par les deux premières composantes principales sur les variables explicatives.
contrôle des résidus
Pour terminer l’analyse et procéder aux prévisions par intervalles de confiance, il faut procéder au contrôle des résidus.
La répartition des résidus ne doit pas être trop éloignée de la loi normale. Pour vérifier cette hypothèse, nous nous limitons à l’étude de l’histogramme, des coefficients d’asymétrie et d’aplatissement et effectuons un test d’ajustement du c2.
L’histogramme ci-dessous ne montre pas de résidus particulièrement élevés en valeur absolue. Il possède une légère asymétrie, que l’on peut contrôler en examinant le coefficient d’asymétrie :
cas = -0.280
La valeur trouvée est inférieure en valeur absolue à la valeur limite donnée par la table (0.534 pour un échantillon de taille 50).
On examine ensuite le coefficient d’aplatissement :
cap = 2.957
Il est compris entre les valeurs limites données par la table (2.15 et 3.99). Il est même très proche de 3.
Pour effectuer le test d’ajustement du c2, on répartit les observations dans dix classes de même amplitude, et on effectue des regroupements de façon que la condition de convergence de X2 vers la loi du c2 soit satisfaite.
|
Cl. |
% |
Probabilité |
Condition |
|
¦Cl. |
% |
Probabilité |
condition |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0.020 |
0.00820 |
0.41 |
* |
2 |
0.040 |
0.02773 |
1.39 |
* |
|
3 |
0.020 |
0.07914 |
3.96 |
* |
4 |
0.180 |
0.15918 |
7.96 |
|
|
5 |
0.160 |
0.22575 |
11.29 |
|
6 |
0.260 |
0.22575 |
11.29 |
|
|
7 |
0.220 |
0.15918 |
7.96 |
|
8 |
0.040 |
0.07914 |
3.96 |
* |
|
9 |
0.060 |
0.02773 |
1.39 |
* |
10 |
0.000 |
0.00820 |
0.41 |
* |
On regroupe donc les classes 1, 2 et 3, puis 8, 9 et 10. La loi testée étant la loi normale de moyenne nulle et d’écart type estimé, le calcul donne le résultat suivant :
|
Test du c²: x²= 3.1482 |
Ddl: 4 |
Probabilité critique P(X²>x²) = 0.5358 |
On accepte donc l’hypothèse de la loi normale de moyenne nulle.
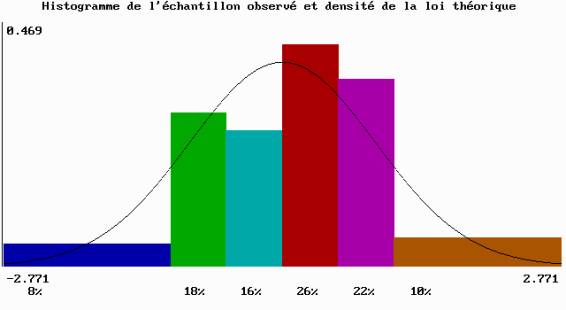
Histogramme des résidus (fichier des données tests dsreg1.dat, 50 observations)
conclusion
Cette étude de cas montre les difficultés à choisir le meilleur modèle de régression possible. Le critère de l’estimation sans biais de la variance résiduelle est discutable, en particulier dans le cas d’une régression sur composantes principales : le meilleur modèle sur le fichier test est celui dont la variance résiduelle est la plus élevée, c’est-à-dire le moins bon au sens du premier critère.
La recherche d’un modèle par sélection des variables explicatives parmi les variables initiales montre aussi ses limites. On notera que le choix du risque de première espèce pour effectuer cette sélection n’est pas facile. Dans cette étude de cas, ce risque exerce une forte influence sur les variables explicatives sélectionnées. En choisissant un risque égal à 20%, on définit le modèle par les trois variables notes de gestion, de langue et d’expression. La moyenne des carrés des résidus calculés sur les données tests est alors égale à 1.20, nettement plus faible qu’en conservant uniquement les notes de gestion et de langue sélectionnées avec un risque de première espèce égal à 10%.
Enfin, nous avons décidé d’éliminer la composante principale C4, malgré un coefficient de corrélation avec la note d’économie significatif pour un risque de 10% : cette décision est prise en considération de la taille de la valeur propre correspondante. Il existe un algorithme permettant de calculer approximativement le coefficient de corrélation minimum pour introduire la composante principale en tenant compte simultanément de l’erreur de première espèce (écarter une composante principale significative) et de celle de seconde espèce (introduire une composante principale non significative). Cet algorithme, trop compliqué pour être présenté ici[1], donne comme système de prédicteurs les trois composantes principales C1, C2 et C4, produit aussi par le critère de Mallows. Ce modèle est nettement meilleur sur les données initiales (fichier DSREG0.DAT) et nettement moins bon sur le fichier test (DSREG1.DAT) que dans le cas des deux composantes principales C1 et C2, ce qui confirme apparemment l’interprétation de C4 comme bruit blanc. Cette interprétation est renforcée aussi par la petite taille (0.08) du coefficient de corrélation entre la composante principale C4 et la variable expliquée Y (note d’économie) dans le fichier test. Le modèle constitué des trois composantes principales C1, C2 et C4 reste toutefois meilleur que les deux autres, définis par l’ensemble des variables initiales et les deux variables gestion et langue. Enfin, dans le modèle défini par les composantes principales C1 et C2, les coefficients de régression des notes de gestion et de maths. sont très proches l'un de l'autre et hautement significatifs. Par contre, les coefficients de régression des notes d’expression et de langue sont faibles et non significatifs. Ces coefficients sont cohérents avec la matrice de corrélation.
Finalement, la note d’économie dépend quasiment uniquement de celles de gestion et de mathématiques. Plus exactement, les notes de gestion et de mathématiques sont suffisantes pour reconstruire la note d’économie aussi bien que possible compte tenu des données.