ANAlyse de l’hérédité
étude de cas commentée

L’étude de cas que nous proposons ici a pour but de retrouver statistiquement des résultats concernant les facteurs héréditaires bien connus des généticiens. Les données sont suffisamment nombreuses pour que l’on puisse leur appliquer un grand nombre des méthodes présentées dans le chapitre sur la régression linéaire multiple.

Ces données et les paramètres figurent sur les fichiers hereditf.dat et hereditf.par (répertoires data et datapar). Ce sont des données réelles ; elles concernent 90 jeunes filles, leurs pères et leurs mères. On distingue trois groupes de variables :

· la taille, le poids et la pointure des jeunes filles elles-mêmes ;

· la taille, le poids et la pointure de leurs pères ;

· la taille, le poids et la pointure de leurs mères.

On note la particularité de la pointure parmi ces variables, qui est donnée en nombre entier.

L’approche que nous proposons dans l’étude de cas « analyse de l’hérédité par l’analyse canonique » consiste à analyser les relations entre la taille, le poids et la pointure des jeunes filles et les mêmes variables concernant leurs parents ; ici, on ne cherche à étudier que le facteur héréditaire dans la taille des étudiantes, qui est donc la variable expliquée. Les six variables explicatives sont alors la taille, le poids et la pointure de leurs parents.

Toutes les analyses concernant ces données peuvent être effectuées sur les données analogues concernant des jeunes de 20 ans de sexe masculin et figurant sur les fichiers hereditm.dat et hereditm.par. Mais le plus petit nombre d’observations (63) est un peu gênant et limite les conclusions auxquelles on aboutit .

La première démarche indispensable consiste à examiner les données. Les résultats statistiques élémentaires sont donnés ci-dessous :

Tableau 1 : Moyennes variances et corrélations

de la taille, du poids et de la pointure des étudiantes, de leurs pères et de leurs mères

Effectif considéré : 90

		Minimum	Maximum	Moyenne	Variance	Ecart-type
Étudiantes	Taille	148	175	163.978	32.200	5.674
	Taille	160	180	169.789	29.300	5.413
Pères	Poids	50	92	71.767	57.423	7.578
	Poids	38	45	41.639	2.095	1.447
	Taille	146	175	160.467	33.560	5.793
Mères	Poids	40	80	57.856	51.612	7.184
	Pointure	35	42	38.217	2.167	1.472

Tableau 2 : Matrice des corrélations de la taille des étudiantes,

de la taille, du poids et de la pointure de leurs pères et de leurs mères

		J.F.		Pères			Mères
		Taille	Taille	Poids	Pointure	Taille	Poids	Pointure
J.F.	taille	1.000
	Taille	0.438	1.000
Pères	Poids	0.168	0.448	1.000
	Pointure	0.288	0.474	0.370	1.000
	Taille	0.427	0.208	0.097	0.126	1.000
Mères	Poids	0.116	-0.187	-0.012	-0.046	0.286	1.000
	Pointure	0.173	-0.105	-0.095	-0.232	0.515	0.376	1.000

On peut effectuer les représentations graphiques des couples d’observations comme (Taille, Poids) pour détecter les unités statistiques aberrantes, mais cela nécessite beaucoup de graphiques (21 en tout) ; le mieux est d’effectuer l’analyse en composantes principales des données constituées des variables explicatives (ici, la taille, le poids et la pointure des parents) et de la variable expliquée (la taille de l’étudiante) ; les plans principaux donnés par cette méthode sont en effet des représentations graphiques des unités statistiques, prennent en compte toutes les variables, et conservent assez bien les distances. On pourra donc distinguer sur ces plans les unités statistiques particulièrement différentes des autres. Nous laissons au lecteur le soin d’effectuer cette ACP très classique qu’il trouvera

On peut utiliser aussi l’analyse en composantes principales pour calculer la courbe de régression de la taille Y des étudiantes par les variables explicatives : on calcule ici les composantes principales des six variables explicatives, puis la courbe de régression de Y par chaque composante principale.

Nous avons effectué ces calculs en regroupant les observations suivant 5 intervalles de même amplitude définis sur la première composante principale. On lit dans le tableau ci-dessous qu’il y a 6 observations dont la première composante principale est dans la première classe, 25 dans la deuxième classe, 35 dans la troisième etc...On calcule ensuite la moyenne et l’écart-type de la variable expliquée Y sur ces 6 observations, puis sur les 25, les 35 etc.... La taille moyenne et la composante principale varient en sens inverse l’une de l’autre :

Tableau 2 : courbe de régression de la taille

par la première composante principale

	Classe	Effectif	Moyenne	Écart-type
1	[-3.448, -2.050[	6	167.67	4.78
2	[-2.050, -0.651[	25	165.20	5.59
3	[-0.651, 0.748[	35	163.37	5.90
4	[0.748, 2.146[	15	162.93	5.31
5	[2.146, 3.545[	9	162.22	4.24

Le rapport de corrélation est défini par le rapport de la variance pondérée des moyennes à la variance totale. Il est ici égal à 0.0608. Le coefficient de corrélation de la variable expliquée et de la première composante principale est égal à -0.262, et son carré (0.0686) est très voisin du rapport de corrélation, ce qui laisse penser que la liaison est linéaire (le test du lack of fit pour vérifier l’hypothèse de linéarité consiste à comparer ces deux valeurs. Il n’est pas expliqué dans le cours et nous ne l’avons pas effectué).

Les moyennes sont régulièrement décroissantes. La courbe de régression (figure 1) est constituée de points relativement bien alignés. L’analyse graphique aboutit donc à la même conclusion.

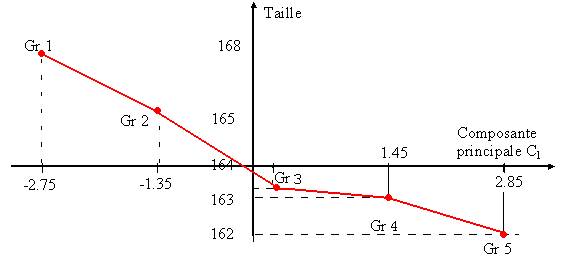
Figure 1 : courbe de régression de la taille des étudiantes

par la première composante principale des variables explicatives

Pour effectuer une régression linéaire simple, on choisit de préférence comme variable explicative celle dont le coefficient de corrélation avec la variable expliquée est le plus élevé en valeur absolue. Un algorithme effectuerait un choix purement numérique, et proposerait la taille du père et non celle de la mère. En examinant la matrice, on constate qu’il n’y a en réalité aucune raison objective, les deux coefficients de corrélation étant très proches l’un de l’autre (0.44 et 0.43). Par contre, le coefficient de corrélation entre la taille du père et celle de la mère est assez faible (0.21) : ces deux variables apportent des informations complémentaires, et nous y reviendrons.

Choisissons comme première variable explicative la taille du père et calculons les coefficients de corrélation partielle.

Les résultats (tableau ) montrent les conséquences de l’introduction de la taille du père comme variable explicative :

· le coefficient de corrélation entre la taille du père et celle de la jeune fille est hautement significatif (la probabilité critique est numériquement nulle : R² = 0.192, F(1, 88 ) = 20.923, P(F>20.923) = 0).

· le coefficient de corrélation partielle entre la taille de la mère et celle de la jeune fille (0.382) est aussi hautement significatif. Cela correspond à l’intuition que nous en avions en examinant la matrice des corrélations (cf. supra).

· Les coefficients de corrélation partielle entre la taille de la jeune fille et le poids ou la pointure de son père sont faibles (pour le poids, on a F =.11, P(F> 0.11) = 0.7436). L’introduction de la taille du père a pris en compte toute l’hérédité paternelle.

· Les coefficients de corrélation partielle entre le poids et la pointure de la mère et la taille de sa fille ont augmenté et sont devenus significatifs (pour le poids, on a F = 4.6 et P(F > 4.6) = 0.033). Toutes les variables concernant la mère contribuent à la taille de sa fille.

Tableau 3 : Analyse des coefficients de corrélation partielle

conditionnellement à la taille du père

Variables explicatives considérées : taille Père

R²	F( 1, 88 )	Prob.crit.	Variance résiduelle estimée
0.19209	20.9229	0.0000	26.606

Coefficients de détermination de chaque variable par rapport aux variables explicatives :

Pères		Mères
poids	pointure.	taille	poids	pointure
0.200	0.225	0.043	0.035	0.011

Coefficients de corrélation partielle avec la taille de la J.F.:

Pères		Mères
poids	pointure.	taille	poids	pointure
-0.035	0.101	0.382	0.224	0.246

Test sur le coefficient de corrélation partielle maximal (taille Mères)

Coefficient	Probabilité critique
0.382	0.00

Pour choisir une deuxième variable explicative, on considère celles dont les coefficients de corrélation partielle sont les plus grands en valeur absolue, et, parmi elles, on élimine celles dont le coefficient de détermination avec les variables explicatives déjà introduites est très élevé. Il n’existe aucune difficulté ici : on introduit la taille de la mère comme deuxième variable explicative. On calcule ensuite les nouveaux coefficients de corrélation partielle, conditionnellement à la taille du père et à celle de la mère :

Tableau 4 : Analyse des coefficients de corrélation partielle

conditionnellement à la taille du père et à celle de la mère

Variables explicatives considérées : taille Père, taille Mère

R²	F( 1, 88 )	Prob.crit.	Variance résiduelle estimée
0.31014	19.5563	0.0000	22.979

Coefficients de détermination de chaque variable par rapport aux variables explicatives :

Pères		Mères
poids	pointure.	poids	pointure
0.200	0.225	0.145	0.312

Coefficients de corrélation partielle avec la taille de la J.F.:

Pères		Mères
poids	pointure.	poids	pointure
-0.040	0.096	0.109	0.045

Test sur le coefficient de corrélation partielle maximal (poids Mères)

Coefficient	Probabilité critique
0.109	0.3116

Les résultats ci-dessus sont assez clairs : aucun coefficient de corrélation partielle n’est plus significatif, et il n’y a pas lieu d’introduire une nouvelle variable explicative. L’introduction de la taille de la mère comme variable explicative prend en compte toute l’hérédité maternelle, comme cela s’est produit pour le père.

En fait, nous avons effectué à la main l’algorithme de régression ascendant en contrôlant la colinéarité à l’aide du coefficient de détermination des variables par rapport aux variables explicatives déjà introduites et constaté qu’il ne cache aucune propriété particulière due au critère numérique utilisé.

Le choix des variables explicatives est donc terminé : il montre l’existence, concernant la taille des jeunes filles, de deux facteurs héréditaires, caractérisés par la taille de son père et par celle de sa mère. On notera que tous les tests précédents ne sont jutifiés que si les résidus sont distribués suivant la loi normale, hypothèse qu’il sera donc indispensable de vérifier lorsqu’ils auront été calculés. Le modèle de régression est le suivant :

Taille J.F. » 0.3829 Taille Père + 0.3441 Taille Mère + 43.7568

Nous donnons dans le tableau 5 les résultats statistiques complets de la régression. Tous les coefficients de régression sont très significatifs, puisque le T de Student est largement au-dessus de la valeur critique 2 (exactement 1.96 puisque pour 90 observations, la loi de Student est confondue avec la loi normale centrée réduite) ; la valeur 0 n’appartient d’ailleurs pas aux intervalles de confiance. Le modèle de régression est donc a priori satisfaisant.

Tableau 5 : Résultats numériques de la régression linéaire

Variable	Estimation	Ecart-type	T de Student	Intervalle de confiance
taille Père	0.3829	0.0954	.012	[0.1959, 0.5699]
Taille Mère	0.3441	0.0892	3.858	[0.1693, 0.5189]
Constante	43.7568

On observe que plus l’un des parents est grand, plus sa fille est grande, et ces deux effets s’ajoutent dans les mêmes proportions puisque les coefficients de régression sont presqu’égaux. Mais le fait que leur somme soit inférieure à 1 montre que l’écart à la moyenne a tendance à diminuer d’une génération à la suivante : la taille est un caractère héréditaire récessif. Donnons un exemple concret pour expliquer ce que cela signifie : lorsque les parents mesurent dix centimètres de plus que la moyenne des personnes de leur âge, leur fille aura tendance à mesurer un peu plus de sept centimètres de plus que celles de son âge (0.3829 x 10 + 0.3441 x 10 cm).

Le tableau ci-dessous donne les paramètres statistiques habituellement regroupés sous le nom d’analyse de variance.

Tableau 6 : Analyse de variance

	Degrés	Somme des	Variance	Pourcentage de
	de liberté	Carrés	Estimée	de variance totale
Totale	89	2897.956	32.5613	1.0000
Expliquée	3	898.774	9.5822	0.3101
Résiduelle	87	1999.200	22.9800	0.6899
R^2	2,87	R^2 = 0.3101	F(2,87) = 19.556	P(F>19.556)=0.000

Le coefficient de détermination est très significatif, à peine inférieur au coefficient de détermination obtenu par le modèle complet constitué des six variables taille, poids et pointure des deux parents (0.329). La variance résiduelle estimée est légèrement inférieure (22.98 au lieu de 23.43). Le plus gros avantage est que ce modèle incomplet comporte beaucoup moins de variables explicatives (2 au lieu de 6).

Pour valider le modèle et en particulier justifier tous les tests sur les coefficients de corrélation ou les T de Student, et les intervalles de confiance, il reste à examiner les résidus et à vérifier qu’ils suivent approximativement la loi normale.

Parmi les résidus réduits, 3 d’entre eux seulement sont supérieurs en valeur absolue à 1.96, et tous sont inférieurs à 3 : cela correspond à la normalité de la distribution. Les distances de Cook calculées par le logiciel sont très faibles, inférieures à 0.11, et il n’apparaît donc pas d’unité statistique qui perturberait les estimations.

Nous donnons ci-dessous, en figure 2, l’histogramme des résidus réduits répartis en 5 classes de même amplitude.

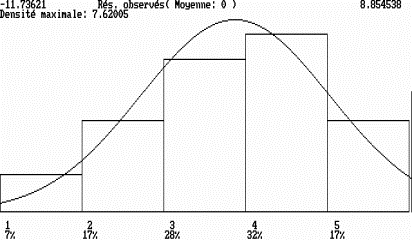
Figure 2 : Histogramme des résidus observés (5 classes de même amplitude)

et densité de la loi normale de mêmes paramètres

La courbe superposée à l’histogramme est la densité de la loi normale centrée réduite : elle lui est visiblement très proche et la normalité de la variable résiduelle est assez évidente (un test d’ajustement du c² ou un test de Kolmogorov donnent comme décision l’acceptation de l’hypothèse d’une loi normale centrée réduite avec des probabilités critiques de l’ordre de 0.85 et 0.55 respectivement. Ces tests ne sont qu’approximatifs).

En outre, les distributions de la taille du père et de la taille de la mère sont elles-mêmes normales, et l’hypothèse d’un modèle multinormal, qui justifie théoriquement l’hypothèse de normalité des résidus, est très vraisemblable.

Ce modèle permet donc d’effectuer des prévisions dans de bonnes conditions ; nous en donnons ci-dessous quelques exemples commentés.

Considérons tout d’abord la taille des jeunes filles dont le père mesure 1.75m et la mère 1.65m :le logiciel StatpC donne les résultats suivants :

Tableau 7 : Première prévision

Variable	Moyenne	écart-type	valeur
TailP	169.788889	5.412936	? 175
TailM	160.466667	5.793099	? 165
	Prévision	Ecart-type	Interv. de conf. (95%)
Taille	167.532805	0.763192	166.006420, 169.059189
			157.824754, 177.240856

Les parents de la jeune fille sont donc plus grands que la moyenne, et l’écart est de l’ordre de l’écart-type. Les résultats signifient que :

· Les jeunes filles dont le père mesure 1.75m et la mère 1.65m mesurent en moyenne 1.675m. Plus précisément, cette moyenne est comprise entre 1.66 et 1.69m.

· La plupart –environ 95%- mesurent entre 1.58m et 1.77m .

Une réaction courante des utilisateurs débutants de la régression est de penser que finalement, la méthode n’apporte guère d’information précise sur la taille des jeunes filles, compte tenu du dernier intervalle de confiance. Ils oublient simplement que la taille d’une jeune fille est loin d’être déterminée totalement par celles de ses parents.

Tableau 8 : Deuxième prévision

Variable	moyenne	Écart-type	valeur
TailP	169.788889	5.412936	? 180
TailM	160.466667	5.793099	? 170
	Prévision	Ecart-type	Interv. de conf. (95%)
Taille	171.167568	1.258228	168.651113, 173.684023
			161.255507, 181.079629

La deuxième prévision que nous avons effectuée concerne les jeunes filles dont les parents mesurent 10 cm de plus que la moyenne. Leur taille moyenne est de 1.71m, environ 7cm de plus que la moyenne, conformément à ce que nous avons dit précédemment, et se rapproche de la taille moyenne 1.64m. On constate en outre que l’écart-type de la prévision est supérieur au précédent. C’est une propriété générale : plus les valeurs des variables explicatives s’écartent des moyennes, moins la prévision est précise.

Tableau 9 : Troisième prévision

Variable	Moyenne	Écart-type	valeur
TailP	169.788889	5.412936	? 160
TailM	160.466667	5.793099	? 150
	Prévision	Ecart-type	Interv. de conf. (95%)
Taille	156.628515	1.279284	154.069946, 159.187084
			146.705679, 166.551351

Cette troisième prévision montre que le caractère récessif de la taille joue aussi dans l’autre sens : les parents mesurent 10 cm de moins que la moyenne, mais leur fille 7.36 cm de moins.

L’intérêt de cette étude de cas est en un certain sens la confiance qu’elle donne à l’utilisateur dans l’analyse statistique des données : il est rassurant en effet de vérifier qu’elle met en évidence des propriétés qui sont bien connues des spécialistes. On aurait pu poursuivre l’analyse en effectuant des tests sur les coefficients de régression, en vérifiant par un test statistique que leur somme est inférieure à 1, et donc que la taille est un caractère récessif indépendamment des données observées, ou encore qu’ils sont égaux, et donc que l’hérédité maternelle intervient autant que l’hérédité paternelle. Les procédures deviennent trop compliquées pour qu’on puisse les développer ici.

On pourra enfin utiliser ces donnéer pour appliquer d’autres méthodes de régression, en particulier la régression sur composantes principales et la régression pas à pas.