Algorithme de Simulation de la Loi binormale
Il s’agit
ici d’expliquer l’algorithme utilisé dans la plupart des cas pour simuler
un échantillon de la loi binormale. On
suppose connues les procédures de simulation d’une loi uniforme et d’une loi
normale pexpliquées dans une autre application du chapitre 5.
La densité
la plus connue d’un couple de (X,Y) de variables aléatoires est la loi
binormale. Lorsque les v.a. X et Y sont centrées et réduites, on a :
|
mx = 0 |
sx = 1 |
my = 0 |
sy = 1 |
Soit r le coefficient de corrélation des v.a. X et
Y. La densité du couple (X, Y) est donnée par la formule ci-dessous :
Un grand nombre de test statistiques, par exemple le test du F sur le
coefficient de corrélation (cf. chapitre 6), sont fondés sur l’hypothèse que le
couple (X, Y) suit la loi binormale. La simulation de la loi binormale permet
concrétiser ces tests et leurs résultats.
La procédure
de simulation repose sur une propriété fondamentale : la moyenne E(Y / X = x) de la
variable Y pour une valeur x de X fixée est une fonction linéaire de x. Cette
propriété s’exprime de la façon suivante :
E(Y / X = x) = b x +
a
|
ou encore : |
Y = b x + a
+ |
|
avec : |
b = r sy/sx = r |
|
|
a = my – b mx = 0 |
La v.a. e suit la loi normale d’espérance nulle et de variance 1 – r2, puisque par hypothèse la variance de la v.a. Y est égale à 1. Elle est indépendante de X. On en déduit :
Y = r X + [ (1 – r2)] 1/2 Z
avec les conditions suivantes :
· X suit la loi normale centrée réduite
· Z suit la loi normale centrée réduite.
· X et Z sont indépendantes.
Dès lors, la simulation est simple :
· on génère une valeur x suivant la loi normale centrée réduite ;
· on génère une valeur z suivant la loi normale centrée réduite ;
· on pose :
|
y = r x + [ (1 – r2)] 1/2 z |
Le couple (x, y) est une réalisation du couple (X,Y) de loi binormale, dont les v.a. X et Y suivent la loi normale centrée réduite et dont le coefficient de corrélation est égal à r.
On peut déduire du couple (X,Y) un couple (X’,Y’) de moyenne et de variance quelconques mX’, sX’ et mY’, sY’ en effectuant les simples transformations linéaires :
|
X’ = sX’X + mX’ |
Y’ = sY’Y + mY’ |
Le logiciel donne la liste des couples simulées et la représentation graphique pour un coefficient de corrélation donné. La multiplication des expériences montre que le coefficient de corrélation observé est plus ou moins proche du coefficient de corrélation théorique et que la forme du nuage de points est liée au coefficient de corrélation :
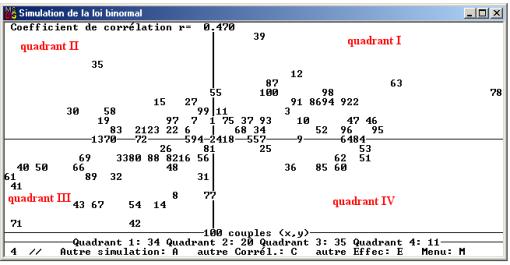
Cette forme est d’autant plus stable que
l’effectif est important. Elle s’explique par la répartition des observations
dans les quatre quadrants du plan, indiquée en bas de l’écran (34 dans le
quadrant I, 20 dans le quadrant II, 35 dans le quadrant III, et 11 dans le
quadrant IV sur le schéma ci-dessus).
Il est possible de tirer le coefficient de
corrélation au hasard : le jeu est alors d’en donner une valeur approximative.
Cette dernière procédure est systématisée dans le logiciel TESTEAO (test de
Fisher sur le coefficient linéaire) et expliquée en détail dans l’ouvrage
Introduction aux tests statistiques, Enseignement assisté par ordinateur, T.
Foucart, Technip, 1991.