Devoir surveillé de Statistiques
(1e année, 28/01/2005)
On remettra l’annexe après avoir complété les tableaux. Toutes les réponses doivent être rapidement justifiées sur une feuille à part contenant également les graphiques (une justification graphique est parfois suffisante). On enlèvera un point pour chaque faute d’orthographe. La présentation des résultats et la qualité de la rédaction interviennent notablement dans la note définitive.
I. On considère une série de 500
observations comprises entre 0 et 20.
1) Déterminer à l’aide du graphique donné en annexe la médiane, les quartiles et les déciles d1 et d9.
2) On donne en annexe la représentation graphique de la fonction de concentration C(p) calculée sur la série (xi) i=1, …, 500. Déterminer graphiquement, pour chaque valeur p ci-dessous, la valeur de la fonction de concentration C(p) correspondante :
|
p = |
0.1 |
0.3 |
0.5 |
0.7 |
0.9 |
|
C(p) = |
|
|
|
|
|
3) Déterminer graphiquement le pourcentage p d’observations les plus petites dont la somme représente une proportion C(p) de la somme totale :
|
p = |
|
|
|
|
|
C(p) = |
0.2 |
0.4 |
0.6 |
0.8 |
4) Déterminer graphiquement le pourcentage q d’observations les plus plus grandes dont la somme représente une proportion C’(q) de la somme totale :
|
q = |
|
|
|
|
C’(q) = |
0.25 |
0.5 |
0.75 |
II. On considère la série de 25
observations (xi) i = 1, …, 25 donnée en annexe.
1) Calculer la fonction de répartition F(x) pour les valeurs de x données dans le tableau figurant en annexe.
Représenter graphiquement la fonction de répartition (on se limitera aux points ci-dessus). Déterminer graphiquement la médiane et les quartiles et comparer ces approximations à leurs valeurs calculées sur les observations.
2) Compléter le tableau en annexe donnant la concentration pour chaque valeur de x. Représenter graphiquement la courbe de concentration C(p) aux points p = 0, 0.2, 0.4, 0.6, 0.8, 1.(on effectuera une interpolation linéaire entre les points).
3) Calculer l’aire de la zone comprise entre la courbe de concentration et la droite d’équation y = x, en la découpant en triangles et en trapèzes (on rappelle l’aire d’un trapèze : somme des bases multipliée par hauteur et divisée par 2).
4) En déduire une valeur approchée du coefficient de concentration.
ANNEXE
I.
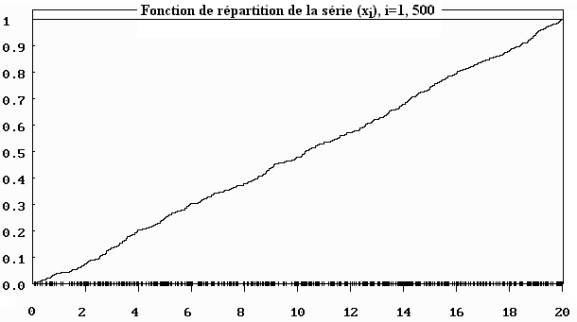
|
médiane = |
q1 = |
q3 = |
d1 = |
d9 = |
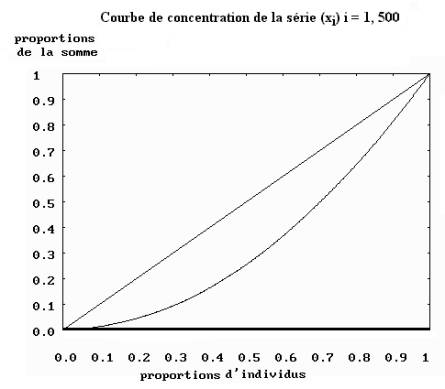
|
p = |
0.1 |
0.3 |
0.5 |
0.7 |
0.9 |
|
C(p) = |
|
|
|
|
|
|
p = |
|
|
|
|
|
C(p) = |
0.2 |
0.4 |
0.6 |
0.8 |
|
q = |
|
|
|
|
C’(q) = |
0.25 |
0.5 |
0.75 |
II. Tableaux concernant la série des 25
observations à compléter :
Liste des 25 observations :
|
0.04 |
0.06 |
0.08 |
0.12 |
0.16 |
|
0.17 |
0.18 |
0.21 |
0.25 |
0.26 |
|
0.33 |
0.50 |
0.63 |
0.64 |
1.12 |
|
1.41 |
1.58 |
1.59 |
1.75 |
2.13 |
|
2.30 |
2.45 |
2.59 |
2.73 |
2.95 |
Tableau de la fonction
de répartition :
|
x |
0 |
0.3 |
0.6 |
0.9 |
1.2 |
1.5 |
1.8 |
2.1 |
2.4 |
2.7 |
3 |
|
F(x) |
|
|
|
|
|
|
|
|
|
|
|
Tableau de la courbe de concentration :
|
n° |
Proportion p |
valeur observée |
somme partielle |
concentration C(p) |
|
1 |
0.04 |
0.04 |
0.04 |
0.00153 |
|
2 |
0.08 |
0.06 |
0.10 |
0.00382 |
|
3 |
0.12 |
0.08 |
0.18 |
0.00687 |
|
4 |
0.16 |
0.12 |
|
0.01145 |
|
5 |
0.20 |
0.16 |
0.46 |
0.01756 |
|
6 |
0.24 |
0.17 |
0.63 |
0.02405 |
|
7 |
0.28 |
0.18 |
0.81 |
0.03092 |
|
8 |
0.32 |
0.21 |
1.02 |
0.03893 |
|
9 |
0.36 |
0.25 |
1.27 |
0.04847 |
|
10 |
0.40 |
0.26 |
1.53 |
0.05840 |
|
11 |
0.44 |
0.3 |
1.83 |
0.06985 |
|
12 |
0.48 |
0.5 |
2.33 |
0.08893 |
|
13 |
0.52 |
0.63 |
2.96 |
0.11298 |
|
14 |
0.56 |
0.64 |
3.60 |
|
|
15 |
0.60 |
1.12 |
4.72 |
0.18015 |
|
16 |
0.64 |
1.41 |
6.13 |
0.23397 |
|
17 |
0.68 |
1.58 |
7.71 |
0.29427 |
|
18 |
0.72 |
1.59 |
|
|
|
19 |
0.76 |
1.75 |
11.05 |
0.42176 |
|
20 |
0.80 |
2.13 |
13.18 |
0.50305 |
|
21 |
0.84 |
2.3 |
15.48 |
0.59084 |
|
22 |
0.88 |
2.45 |
17.93 |
0.68435 |
|
23 |
0.92 |
2.59 |
20.52 |
0.78321 |
|
24 |
0.96 |
2.73 |
23.25 |
0.88740 |
|
25 |
1.00 |
2.95 |
26.20 |
1.00000 |