Thierry Foucart

Département TC

Châtellerault

Devoir surveillé de Statistiques

(1^e année, 23/05/2005)

La qualité de la présentation, de la rédaction et l’orthographe seront prises en compte de façon importante dans l’évaluation globale du travail rendu.

On considère deux séries chronologiques.

I. Les graphiques sont donnés ci-dessous :

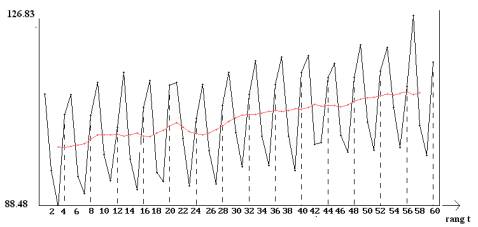
Figure 1 : représentation graphique de la série 1

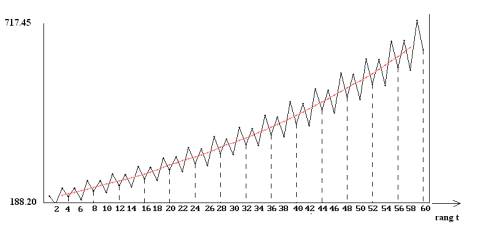
Figure 2 : représentation graphique de la série 2

Commenter ces deux graphiques.

II. On considère les 20 premières observations de la série 1 :

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990	111.11	95.75	88.48	106.96
1991	110.94	94.65	91.16	106.79
1992	113.44	98.99	93.69	104.48
1993	115.45	98.12	91.90	108.39
1994	113.82	95.39	93.64	112.85

Valeurs observées

1) En utilisant la représentation graphique précédente et les résultats numériques ci-dessous, justifier le modèle additif et calculer les coefficients saisonniers.

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990
1991	100.59	100.90	101.19	102.05
1992	102.91	102.93	102.90	103.04
1993	102.71	102.97	103.26	102.71
1994

moyennes mobiles de longueur 4

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990
1991	10.34	-6.25	-10.03	4.73
1992	10.52	-3.94	-9.21	1.43
1993	12.73	-4.85	-11.36	5.67
1994

différences observations - moyennes mobiles

L’observation du premier trimestre 1995 est égale à 113.39. Que peut-on en dire par rapport au dernier trimestre 1994 ?

2) On donne ci-dessous les moyennes annuelles m_T et des résultats numériques :

année	T	moyenne mT
1990	1	100.57
1991	2	100.88
1992	3	102.64
1993	4	103.46
1994	5	103.92
		Sommes
des observations T		15
des observations mT		511.5
des carrés T²		55
des carrés mT²		52335.55
des produits T x mT		1543.78

Effectuer la régression linéaire de de la moyenne annuelle m_T, par l’année numérotée de T = 1 à T = 5. En déduire les prévisions de la moyenne annuelle pour les années suivantes, de 1995 à 2000. Que peut-on dire de ces prévisions ?

année	T	moyenne mT
1995	6	103.61
1996	7	103.64
1997	8	106.58
1998	9	107.55
1999	10	108.13
2000	11	108.92

III. On considère les 20 premières observations de la série 2 :

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990	210.86	188.20	234.06	208.73
1991	234.38	200.66	254.62	224.98
1992	254.72	222.01	274.31	241.68
1993	272.83	237.72	295.09	261.29
1994	293.70	257.24	320.96	286.29

Valeurs observées

1) En utilisant la représentation graphique précédente et les résultats numériques ci-dessous, justifier le modèle multiplicatif et calculer les coefficients saisonniers.

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990
1991	222.02	226.62	231.20	236.41
1992	241.54	246.09	250.44	254.67
1993	259.23	264.28	269.34	274.39
1994

moyennes mobiles de longueur 4

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990
1991	12.35	-25.96	23.41	-11.43
1992	13.17	-24.08	23.86	-12.99
1993	13.59	-26.56	25.74	-13.10
1994

différences observations - moyennes mobiles

années	1^er trimestre	2^etrimestre	3^e trimestre	4^e trimestre
1990
1991	1.05	0.88	1.10	0.95
1992	1.05	0.90	1.09	0.94
1993	1.05	0.89	1.09	0.95
1994

rapports observations / moyennes mobiles

L’observation du premier trimestre 1995 est égale à 324.32. Que peut-on en dire par rapport au dernier trimestre 1994 ?

2) Effectuer la régression linéaire de de la moyenne annuelle m_T, par l’année numérotée de T = 1 à T = 5.

année	T	moyenne mT
1990	1	210.46
1991	2	228.66
1992	3	248.18
1993	4	266.73
1994	5	289.54
		Sommes
des observations T		15
des observations mT		1243.57
des carrés T²		55
des carrés mT²		313150.4
des produits T x mT		3926.94

En déduire les prévisions de la moyenne annuelle pour les années suivantes, de 1995 à 2000. Que peut-on dire de ces prévisions par rapport aux moyennes réelles données ci-dessous  ?

année	T	moyenne mT
1995	6	315.36
1996	7	340.91
1997	8	368.48
1998	9	398.32
1999	10	430.74
2000	11	467.53