Thierry Foucart
Département TC
Châtellerault
Devoir surveillé de Statistiques
(1e année, 14 avril 2006)
Barème (pour des réponses complètes, justifiées rapidement et présentées correctement sans faute de français ni d’orthographe ):
|
1) 2 |
2) 3 |
3) 3 |
4) 3 |
5) 3 |
6) 3 |
7) 3 |
On considère deux variables X et Y dont on dispose de 52 observations (xi,
yi). On trouvera en annexe la représentation graphique de ces
couples, les résultats numériques et les tables statistiques nécessaires pour répondre
aux questions. On conservera le texte et les tables statistiques et on
remettra cette annexe complétée avec la copie. Les justifications des réponses
seront données sur la copie et non sur l’annexe.
1) Calculer les moyennes mX, mY, et les variances sX2, sY2 des variables X et Y et leur covariance cov(X,Y). Que peut-on dire la valeur numérique de la covariance obtenue ?
2) Calculer le coefficient de corrélation linéaire r(X,Y) (on donnera deux décimales). Que peut-on dire de ce coefficient si on multiplie toutes les valeurs xi par 2 et on divise toutes les valeurs yi par 4 ? Ce coefficient de corrélation peut-il être considéré comme grand en valeur absolue ? Montre-t-il l’existence d’une relation linéaire ?
3) Calculer les coefficients b et a de l’équation y = b x + a de la droite de régression de Y par X. Quelle valeur de Y prévoit-on pour x = 2 ? Pour x = – 2 ? Que peut-on dire de ces prévisions ?
4) Quelle est la moyenne des résidus ? Leur variance ? On donne les observations ci-dessous :
|
i |
xi |
yi |
|
6 |
1.2873 |
-2.0458 |
|
18 |
0.4225 |
1.0767 |
Calculer les résidus e6 et e18.
5) Construire à l’intérieur du cadre prévu
dans l’annexe l’histogramme des résidus suivant la répartition
ci-dessous :
|
[-2.0 , -0.7 [ |
8 |
|
[-0.7 , -0.3 [ |
5 |
|
[-0.3 , 0.3 [ |
22 |
|
[0.3 , 0.7 [ |
9 |
|
[0.7 , 2.0 ] |
8 |
6) On donne ci-dessous le coefficient d’asymétrie et le coefficient d’aplatissement des résidus :
|
cas = –0.126 |
cap = 2.836 |
Peut-on considérer que les résidus sont répartis suivant la loi normale ?
7) Que peut-on dire des résidus e6 et e18 précédents ?
Résultats
numériques (n = 52 observations) :
|
Somme des observations xi: |
-7.893781 |
des carrés xi²: |
54.22464 |
|
Somme des observations yi: |
7.885101 |
des carrés yi²: |
40.84260 |
|
Somme des produits xiyi: |
-31.41701 |
|
|
Annexe
(à remettre avec le devoir)
Nom |
Prénom |
Groupe |
|
mX
= |
mY
= |
|
sX2
= |
sY2 = |
|
cov(X,Y) = |
r(X,Y) = |
|
b = |
a = |
|
pour x = 2, y = |
Pour x = –2, y = |
|
moyenne des résidus = |
s2 = |
|
e6
= |
e18
= |
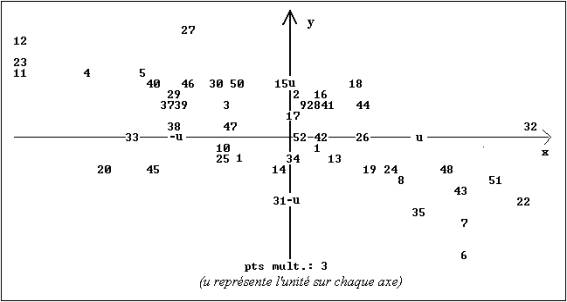
Représentation graphique des couples (xi, yi) i = 1, …52.

Histogramme des résidus ei, i = 1, …52
Tables statistiques
|
n |
valeur limite |
n |
valeur limite |
n |
valeur limite |
|
10 |
0.6319 |
60 |
0.2542 |
150 |
0.1603 |
|
20 |
0.4438 |
70 |
0.2352 |
160 |
0.1552 |
|
30 |
0.3610 |
80 |
0.2199 |
170 |
0.1506 |
|
40 |
0.3120 |
90 |
0.2072 |
180 |
0.1463 |
|
50 |
0.2787 |
100 |
0.1966 |
200 |
0.1388 |
Valeurs limites des coefficients de corrélation
dans le cas de lois normales
|
Coefficient d’asymétrie |
Coefficient d’aplatissement |
||||||
|
Effectif de l’échantillon |
5% |
1% |
Effectif de l’échantillon |
1% |
5% |
95% |
1% |
|
7 |
1.018 |
1.457 |
7 |
1.25 |
1.41 |
3.55 |
4.29 |
|
8 |
0.998 |
1.452 |
8 |
1.31 |
1.46 |
3.70 |
4.53 |
|
9 |
0.977 |
1.433 |
9 |
1.35 |
1.53 |
3.86 |
4.82 |
|
10 |
0.954 |
1.407 |
10 |
1.34 |
1.56 |
3.95 |
5.00 |
|
12 |
0.910 |
1.353 |
12 |
1.46 |
1.64 |
4.05 |
5.20 |
|
15 |
0.851 |
1.272 |
15 |
1.55 |
1.72 |
4.13 |
5.30 |
|
20 |
0.772 |
1.155 |
20 |
1.65 |
1.82 |
4.17 |
5.36 |
|
25 |
0.711 |
1.061 |
25 |
1.72 |
1.91 |
4.16 |
5.30 |
|
30 |
0.662 |
0.986 |
30 |
1.79 |
1.98 |
4.11 |
5.21 |
|
35 |
0.621 |
0.923 |
35 |
1.84 |
2.03 |
4.1 |
5.13 |
|
40 |
0.587 |
0.870 |
40 |
1.89 |
2.07 |
4.06 |
5.04 |
|
45 |
0.558 |
0.825 |
45 |
1.93 |
2.11 |
4.00 |
4.94 |
|
50 |
0.534 |
0.787 |
50 |
1.95 |
2.15 |
3.99 |
4.88 |
|
60 |
0.492 |
0.723 |
|
|
|
|
|
|
70 |
0.459 |
0.673 |
75 |
2.08 |
2.27 |
3.87 |
4.59 |
|
80 |
0.432 |
0.631 |
|
|
|
|
|
|
90 |
0.409 |
0.596 |
|
|
|
|
|
|
100 |
0.389 |
0.567 |
100 |
2.18 |
2.35 |
3.77 |
4.39 |
Valeurs limites des coefficients d’asymétrie et d’aplatissement
dans le cas de lois normales