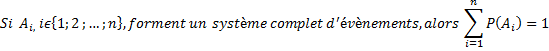A, B,... sont des évènements.

Les propriétés sont admises.

Il peut être pertinent pour ceux qui sont très réfractaires à la théorie de traduire en langage courant avec des pourcentages (voir les exemples).

P(Ā)=1-P(A).

Si vous avez 70% de chances de gagner un match, vous avez 30% de chances de ne pas le gagner.

Ce type de calcul est utile lorsque l'évènement initial A est compliqué, il peut alors être plus simple d'utiliser l'évènement contraire. 

Pour tous les évènements A, on a 0≤P(A)≤1

Le pourcentage de chances qu'un évènement arrive est positif ou nul et ne peut être plus grand que 100% .

P(Ø)=0

Le pourcentage de chances que l'évènement impossible arrive est égal à 0.

Si AcB, alors P(A)≤ P(B).

Si à chaque fois que A est réalisé, alors B l'est aussi, le pourcentage de chances que B arrive est plus grand que celui de A.

Attention !

Nous avons déjà donné la probabilité de la réunion de deux évènements dans la définition. Mais nous l'avons fait pour des évènements disjoints. 

Ici, il s'agit de deux évènements A et B quelconques, pas forcéments disjoints. Dans le cas général nous avons donc :

Remarquons que si AnB=Ø, alors P(AnB)=0 et on retrouve la définition.

Dans le cas d'un système complet d'évènements, tous sont disjoints 2 à 2 et la réunion est égale à l'univers.