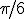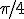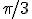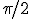Le cercle trigonométrique
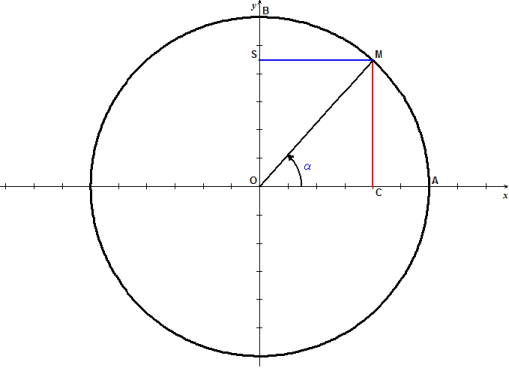 |
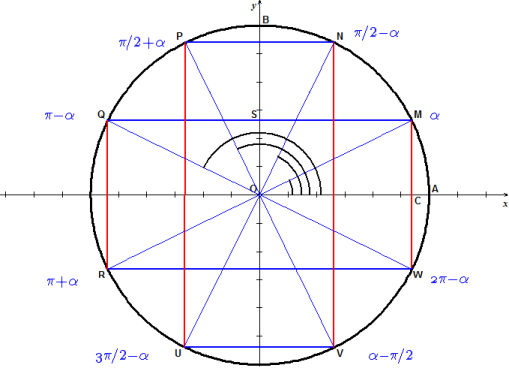
Le cercle trigonométrique a pour rayon 1.
Donc, Ici, l'unité vaut 6 graduations. L'angle α est un angle orienté, dont la mesure est exprimée habituellement en radians. Elle peut aussi être exprimée en degrés et plus rarement en grades.
Si x est la mesure en
radians, y la mesure en degrés et z la mesure en grades, On définit alors : On confond très souvent (car c'est bien commode) le cosinus ou le sinus de l'angle α et le cosinus ou le sinus de sa mesure x ou y. On écrit alors pour des mesures en radians :
|
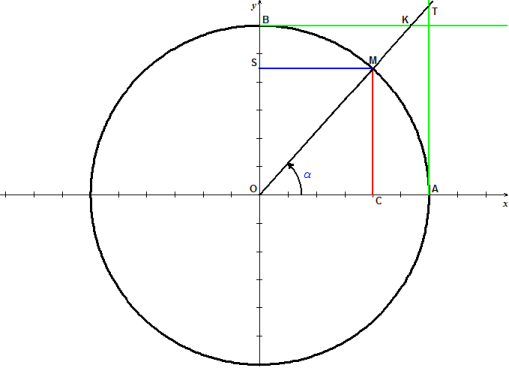 |
On peut aussi définir à partir du cercle trigonométrique : On confond là encore la tangente ou cotangente de l'angle α avec la tangente ou cotangente de sa mesure x. On a alors : Notons que l'on définit aussi tangente et cotangente de la façon suivante :
|
|
|
α est la mesure de l'angle en radians.
|
|
|
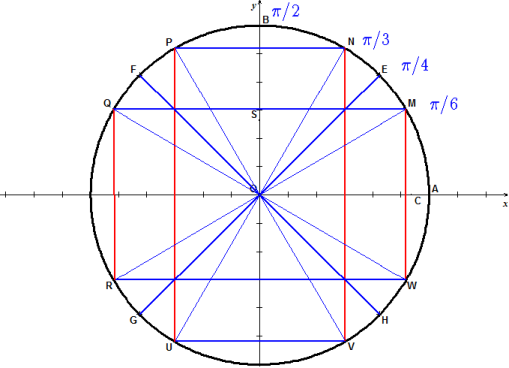
Vous pouvez compléter en calculant les mesures des angles correspondants aux points P,F,Q,R,G,U,V,H,W de la figure ci-contre et en écrivant les valeurs des sinus, cosinus, tangente et cotangente. Aidez-vous des symétries des figures précédentes. |