Corrigé 1

f et g sont dérivables comme somme de fonctions dérivable

h est dérivable comme produit de fonctions dérivables

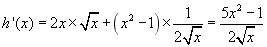
k est dérivable comme inverse d’une fonction dérivable non nul

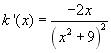
l est dérivable comme quotient de fonctions dérivables

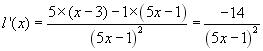
m et n sont dérivables comme quotient et produit de fonctions dérivables

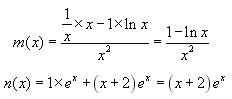
Attention ! Il est préférable de dériver p comme une somme

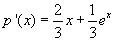
Corrigé 2
La fonction dérivée f’(x) = 2x + 4 permet de déterminer le nombre dérivé :

f’(0) = 4 coefficient directeur de la tangente demandée dont l’équation est :
y = 4(x-0)+f(0)          soit   y = 4x - 2.

 

Cliquer ici pour revenir aux exercices !