Exercice
|
Solution |
Commentaire |
|

|
\blue \vec V=\vec U
|
|
|
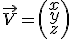
|
\vec V=\left(
\begin{array}
x\\
y\\
z\\
\end{array}
\right)
|
|
|
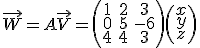
|
\vec W=A \vec V=\left(
\begin{array}
1&2&3\\
0&5&-6\\
4&4&3\\
\end{array}
\right)
\left(
\begin{array} x\\
y\\
z\\
\end{array}
\right)
|
Sauter des lignes permet de clarifier le texte LateX sans changer le résultat |
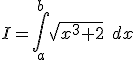 |
I=\int_a^b \sqrt{x^3+2} \; dx |
\; permet d'espacer le dx
si on tape
I=\int_a^b \sqrt{x^3+2} dx
on obtiendra
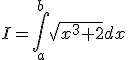
|
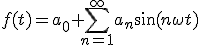 |
f(t)=a_0 +\sum_{n=1}^\infty a_n\sin(n\omega t) |
|
|
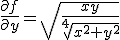
|
\frac {\partial f}{\partial y }= \sqrt {\frac {xy}{\sqrt[4]{x^2+y^2}
|
|
|
|
\left{
\begin{array}
x+y=4\\
x-y=2
\end{array}
\Longleftrightarrow
\left{
\begin{array}
x=3\\
y=1
\end{array} |
|
|
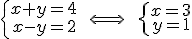
|
\left{
\begin{array}
x+y=4\\
x-y=2
\end{array}
\qquad \Longleftrightarrow
\qquad\left{
\begin{array}
x=3\\
y=1
\end{array |
\qquad permet d'espacer
|
|
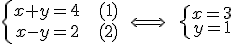
|
\left{
\begin{array}
x+y=4&\qquad (1)\\
x-y=2&\qquad (2)
\end{array}
\qquad \Longleftrightarrow
\qquad\left{
\begin{array}
x=3\\
y=1
\end{array} |
|
|
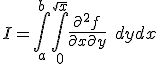
|
I=\int_a^b \int_0^{sqrt{x}} \frac{\part^2 f}{\par x \par y} \; dydx |
|
|
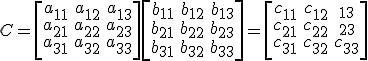
|
C=\left[
\begin{array}
a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}\\
\end{array}
\right]
\left[
\begin{array}
b_{11}&b_{12}&b_{13}\\
b_{21}&b_{22}&b_{23}\\
b_{31}&b_{32}&b_{33}\\
\end{array}
\right]=
\left[
\begin{array}
c_{11}&c_{12}&_{13}\\
c_{21}&c_{22}&_{23}\\
c_{31}&c_{32}&c_{33}\\
\end{array}
\right] |
|
|
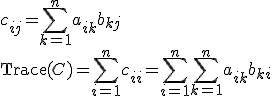
|
c_{ij}=\sum_{k=1}^n a_{ik}b_{kj}\\
\begin{verbatim}Trace\end{verbatim}(C)=\sum_{i=1}^n c_{ii}=\sum_{i=1}^n \sum_{k=1}^n a_{ik}b_{ki} |
|