Echangeurs de chaleur : puissance et efficacité

Exemple de calcul de puissance

Un échangeur à contre courant doit chauffer de l'eau.

Le fluide primaire est de l'eau chaude dont le régime est 55/70°C.

Le fluide secondaire est de l'eau à 20°C, devant être chauffée à 40°C.

Les caractéristique de l'échange sont les suivantes :

  • Coefficient d'échange UD : 41,5 W/m/K

  • Longueur du tube d'échange : 1,5 m

Question

Quelle est l'écart entre la température du fluide primaire et celle du fluide secondaire :

  • à l'entrée de l'échangeur,

  • à la sortie.

Quel est l'écart logarithmique moyen ?

Indice

Les écarts de températures à la sortie et à l'entrée de l'échangeur sont respectivement T0 - t0 et T1 - t1. L'écart logarithmique moyen et donné à la formule [1]

Solution

Ecart à l'entrée = 70 - 40 = 30°C

Ecart à la sortie = 55 - 20 = 35°C

Ecart logarithmique moyen = (30 - 35) / ln (30/35) = 32,4°C

Question

Quelle est la puissance échangée par les deux fluides. On suppose qu'il n'y a pas de pertes de chaleur vers l'air ambiant. Le rendement de l'échangeur est égal à 100%.

Indice

C'est la formule de Hausbrand qui s'applique ici.

Solution

P = pi x 41,5 x 1,5 x 32,4 = 6336 W

Question

On envisage maintenant d'utiliser un échangeur à courants parallèles, toutes choses égales par ailleurs.

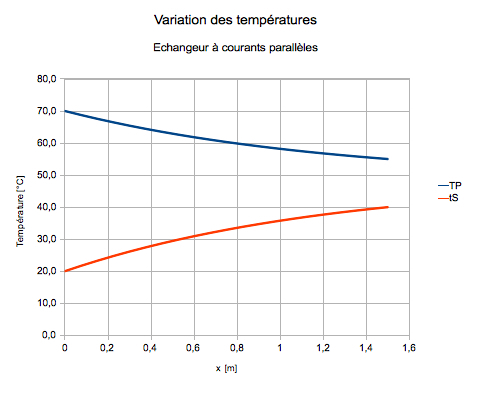
Quelle est l'écart logarithmique moyen dans ce cas ?

Indice

Dans ce contexte, les écarts de températures entre fluides à l'entrée et à la sortie de l'échangeur sont différentes de ceux trouvés pour l'échangeur à courant parallèle.

Solution

Ecart à l'entrée = 70 - 20 = 50°C

Ecart à la sortie = 55 - 40 = 15°C

Ecart logarithmique moyen = (50 - 15) / ln (50/15) = 29,1°C

Question

Quelle et la puissance échangée par l'échangeur à courants parallèles.

Indice

La formule d'Hausbrand s'applique également ici...

Solution

P = pi x 41,5 x 1,5 x 29,1 = 5691 W

RemarqueEfficacité d'un échangeur

La puissance échangée par un échangeur à courants parallèles, toutes choses égales par ailleurs, est moindre que celle échangée par un échangeur à contre courant.

L'échangeur à contre courant est plus efficace que l'échangeur à courants parallèles.

Pour permettre à l'échangeur à courants parallèle de transmettre autant de chaleur que celui à contre courant, on peut opter pour l'allonger.

Question

Quelle doit être la longueur de l'échangeur à courants parallèles si l'on souhaite qu'il échange la même quantité de chaleur que l'échangeur à contre courant ?

Indice

Une règle de trois donne la longeur...

Solution

longueur de l'échangeur à courants parallèles = 6336 / 5691 x 1,5 = 1,67 m

Question

Quelle est la température de sortie du secondaire de l'échangeur à courants parallèles si on lui conserve une longueur d'1,5 m ?

Indice

Un calcul itératif sur la valeur de DELTA 1 permet de résoudre cette question

Solution

L'échangeur à courants parallèles étant moins efficace, la température de sortie doit être moins élevée que prévu :

On fait varier DELTA1 dans la formule de Hausbrand... de manière itérative :

Tentative 1 : DELTA1 = 20 : P = pi x 41,5 x 1,5 x (50 - 20) / ln (50/20) = 6403 W

Tentative 2 : DELTA1 = 17 : P = pi x 41,5 x 1,5 x (50 - 17) / ln (50/17) = 5982 W

Tentative 3 : DELTA1 = 19 : P = pi x 41,5 x 1,5 x (50 - 19) / ln (50/19) = 6265 W

Tentative 4 : DELTA1 = 19,5 : P = pi x 41,5 x 1,5 x (50 - 19,5) / ln (50/19,5) = 6334 W

On peut donc estimer que la température de sortie sera égale à 35,5 °C au lieu de 40°C

PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimerRéalisé avec Scenari (nouvelle fenêtre)