CALCUL INTEGRAL

Calcul d’aires et de volumes

Les intégrales permettent de calculer l'aire d'une surface ou un volume dont la forme ne permet pas un calcul direct à l'aide d'une simple formule. Les seules formes dont on peut calculer simplement l'aire ou le volume sont :

1. Le rectangle

2. Le parallélépipède

Partant de ce constat, le seul moyen de calculer l'aire ou le volume d'une forme plus compliquée que celles ci ne peut être effectué qu'en découpant cette forme en un somme de petits rectangles (dans le cas d'une surface) ou de petits parallélépipèdes (dans le cas d'un volume). Plus les rectangles en question seront petits, meilleure sera la précision. A la limite, ces rectangles doivent être de dimensions les plus proches possibles de zéro. En maths, on appelle ça des longueurs infinitésimales, et on note da une longueur infinitésimale selon le côté a.

 

Rappel

L'outil mathématique qui permet d'additionner des grandeurs infinitésimales est l'intégrale (voir le cours qu'on a fait ensemble à l'IUT).

est la somme des aires de longueur f(x) et de largeur dx en faisant varier x entre a et b :

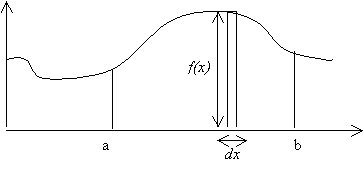
Donc est la somme des rectangles de longueur f(x) et de largeur dx situés entre a et b, c'est à dire l'aire située entre la courbe et l'axe horizontal, délimitée par les traits verticaux issus de a et de b. Le symbole signifie qu'on fait une somme.

 

 

Exemple : Calculer l'aire d'un cercle

Dans ce cas les aires infinitésimales que l'on va sommer (ajouter) sont des couronnes de rayon r et de largeur (infiniment petite) dr :

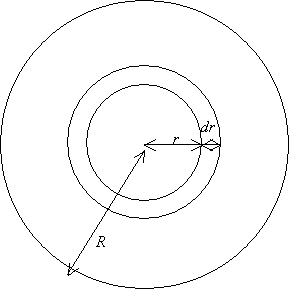
Comment calculer l'aire d'une petite couronne ?

Réponse : Celle ci a une largeur tellement faible que si on la " déroule " on obtient un rectangle de largeur dr et de longueur 2pr. Si la largeur n'était pas très petite, en déroulant la couronne, on n'obtiendrait pas deux longueurs égales : celle située la plus proche du centre aurait une longueur plus faible.

Pour calculer l'aire totale du cercle, il ne reste plus qu'à ajouter les aires de toutes ces couronnes. Pour cela, un calcul d'intégrale est nécessaire :

On voit sur le schéma que la variable r varie entre les valeurs 0 (centre du cercle) à R (bord du cercle), donc les bornes de l'intégrale sont 0 et R.

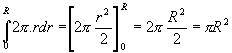
Ce calcul permet bien de déterminer l'aire du cercle puisqu'on reconnaît la formule de l'aire du cercle (pR²).