Structure de l'atome

Classification périodique des éléments

Modèle de Bohr pour l'atome d'hydrogène (1913)

C'est le premier modèle qui se soit véritablement approché de la réalité.

Ce modèle est basé sur la rotation de l'électron autour du proton sur des orbites circulaires.

Il s'appuie par ailleurs sur la théorie des quanta développée par Planck et Einstein en 1905. Selon celle - ci, les échanges d'énergie entre la matière et un rayonnement électromagnétique ne se font pas de manière continue mais par multiple d'une quantité minimale d'énergie E appelée quantum ou énergie du photon.

Cette énergie minimale est donnée par la relation de Planck: E = hn où h est la constante de Planck qui vaut: 6,62 10^-34 Joule.seconde et n est la fréquence du rayonnement électromagnétique qui est absorbé ou émis par la matière.

Bohr fit alors les hypothèses suivantes:

• Dans l'atome d'hydrogène, l'électron se déplace autour du proton uniquement sur des orbites circulaires.

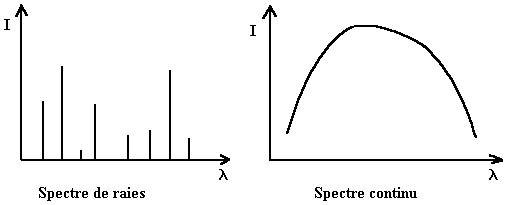
• Le spectre atomique de l'hydrogène étant un spectre de raies, l'échange d'énergie avec cet atome est donc quantifiée sinon ce spectre serait un spectre continu (cf. document ci dessous).

Ceci implique donc que l'énergie de l'atome d'hydrogène ne peut varier continûment mais par sauts. Autrement dit, l'électron ne peut se mouvoir que sur certaines orbites particulières pour lesquelles son énergie est stationnaire.

A chacune de ces orbites correspond une valeur particulière de son énergie.

Lorsque l'électron passe d'un niveau d'énergie E₁ permis à un autre niveau permis E_2, il y a changement d'orbite avec soit absorption ou émission d'un photon.

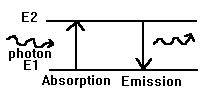
tel que ½ E₂ - E₁ ½ = hn .

• Pour que l'énergie soit quantifiée, il faut que l'une des grandeurs associées à la rotation de l'électron autour du proton soit également quantifiée. Ainsi Bohr imposa (de façon tout à fait arbitraire) et après plusieurs essais, la quantification du moment cinétique orbital de l'électron: ou et sont respectivement la vitesse tangentielle et le rayon de l'orbite. La condition de quantification M = n.(h/2p ) permet le calcul du rayon des orbites et les valeurs permises pour l'énergie de l'électron. On obtient ainsi:

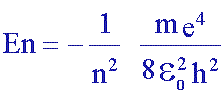avec n = 1, 2, 3, ......

ou m, e, e ₀, et h sont respectivement la masse et la charge de l'électron, la permittivité absolue du vide et la constante de Planck.

n est appelé nombre quantique car il définit la quantification de l'énergie.

(Pour le calcul complet détaillé, cf. document annexe II).

NB. L'énergie de l'électron est négative. Ceci est normal puisque l'énergie acquise par une particule de charge q accélérée par un potentiel V est égale au produit q.V. Or, le potentiel créé par le proton est positif (cf. document annexe II) alors que l'électron est chargé négativement. Ainsi, l'énergie de l'électron est négative.

A n = 1 correspond l'énergie la plus basse. La stabilité de l'édifice proton-électron est alors maximum. Ce niveau d'énergie le plus bas est appelé niveau fondamental.

Les autres niveaux ( n > 1) correspondent à des états excités de l'atome.

A l'échelle atomique, l'énergie est généralement exprimée en électronvolt (symbole eV) car le joule est une unité bien trop grande à cette échelle. L'électronvolt est l'énergie acquise par un électron accéléré par une différence de potentiel égale à un volt soit: 1eV = 1,602 10^-19 Cb x 1V = 1,602 10^-19 joule.

Finalement, en remplaçant m, e, e ₀, et h par leurs valeurs dans l'expression de l'énergie et en convertissant en eV, on trouve:

On peut alors tracer un diagramme des niveaux d'énergie permis pour l'électron de l'atome d'hydrogène:

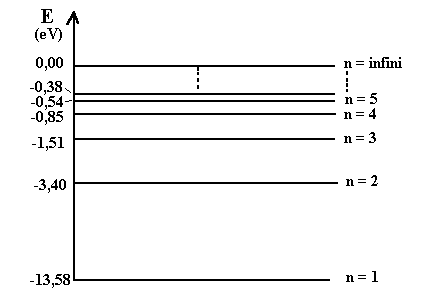
NB. Pour ce diagramme, il n'y a pas d'abscisse, les traits représentent des niveaux. Pour n = 8 , l'électron n'est plus lié au proton. L'atome est ionisé (H⁺).