Structure de l'atome

Classification périodique des éléments

Equation de Schrodinger et spin de l'électron

La résolution de l'équation de Schrodinger n'introduit que les trois nombres quantiques n, l et m. Il fallut attendre 1928 pour que Dirac reprenne l'équation de Schrodinger dans le cadre de la relativité générale d'Einsten pour que s'introduise un quatrième nombre quantique s (pour spin). Celui ci quantifie l'orientation du moment magnétique intrinsèque de l'électron.

L'existence d'un moment magnétique pour l'électron avait déjà été mise en évidence dès 1921 par Stern et Gerlach à l'aide de l'expérience suivante:

Un faisceau d'atomes d'hydrogène traverse un champ magnétique inhomogène produit par les pièces polaires dissymétrique d'un aimant (cf. schéma ci dessous).

Champ magnétique non uniforme Le faisceau se divise en deux

Cette expérience montre que l'électron de l'atome d'hydrogène se comporte comme un petit aimant dont le moment magnétique prend deux orientations privilégiées par rapport au champ magnétique extérieur (celui de l'aimant).

En fait, tout se passe comme si l'électron était une sphère chargée négativement tournant sur elle même dans un sens ou dans l'autre.

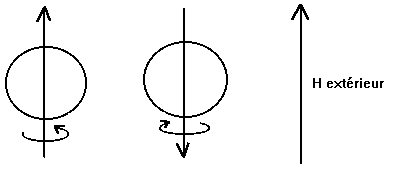Ceci explique que ce soit la lettre s qui ait été choisie comme symbole pour le nombre quantique quantifiant l'orientation du moment magnétique intrinsèque de l'électron (en effet, s est l'abréviation du verbe anglais "spin" qui veut dire tourner).

s ne peut prendre que deux valeurs:

s = +1/2 (­) et s = -1/2 (¯).

Ainsi, l'état d'un électron sera complètement défini lorsque l'on connaît les quatre nombres quantiques ().