Électrotechnique
x x Module 2 : x "Transformateurs" |
Chapitre 2.3
Transformateurs
Régimes particuliers |
1.1 Principe de l'étudeNous prendrons par convention des transformateurs utilisés en abaisser de tension; le primaire sera donc toujours constitué par les enroulements H.T..
L'étude d'un transformateur triphasé fonctionnant en régime déséquilibré est très complexe. La seule méthode permettant l'étude exacte est l'utilisation des composantes symétriques des grandeurs. Ayant décomposé les données en composantes symétriques homopolaire, directe et inverse, nous devons faire l'étude pour chaque système et rechercher les grandeurs inconnues par superposition des états; ceci suppose que la saturation du circuit magnétique ne soit pas atteinte.
Les systèmes direct et inverse étant triphasés équilibrés, l'étude du transformateur peut se faire par la méthode décrite dans ce cas, en utilisant les mêmes éléments du modèle équivalent pour les deux systèmes.
L'étude pour le système homopolaire formé de trois grandeurs égales pour les trois phases est différente. Le fonctionnement du transformateur en régime homopolaire dépend du principe de constitution (3,4,5 colonnes) et du couplage.
Par exemple pour un couplage YNyn , les enroulements primaire et secondaire placés sur un même noyau fonctionnent en régime homopolaire comme un transformateur monophasé.
Pour un couplage Yyn , l'absence de fil neutre au primaire interdit la circulation d'une composante homopolaire des courants primaires (iA +iB +iC = 3.i0p). La composante homopolaire secondaire i0s n'étant pas compensée par les courants primaires, crée dans chaque phase un flux qui se ferme par la ou les colonnes non bobinées si elles existent ou par l'air ou l'huile isolante et la cuve du transformateur à trois colonnes.
Dans le premier cas le courant homopolaire agit comme un courant à vide et se ferme à travers une impédance voisine de celle à vide. Dans le deuxième cas, l'impédance est mal définie; elle est élevée, de l'ordre de 0,7.U2n /I2n.
Lorsque le réseau primaire est équilibré en tension, le déséquilibre des courants de charge secondaire impose des chutes de tensions différentes dans les trois phases et donc déséquilibre les tensions secondaires.
Nous allons adopter le point de vue de l'utilisateur : le transformateur est alimenté au primaire par un réseau triphasé équilibré en tension et alimente une charge secondaire déséquilibrée; quel couplage choisir pour que le déséquilibre des courants secondaires ait le moins d'influence possible sur les tensions secondaires qui doivent rester le plus équilibrées possibles ?
Lorsque les intensités sont déséquilibrées, ce déséquilibre se reporte sur les f.é.m secondaires donc sur les f.é.m primaires; si la somme des f.é.m secondaires ea+eb+ec est différente de 0 en raison du déséquilibre, le couplage triangle est déconseillé au secondaire; en effet les trois f.é.m sont mises en série par le couplage triangle et leur somme crée un courant de circulation dans les phases équivalent à un courant de court-circuit. Nous n'envisageons donc que les couplages étoile ou zigzag au secondaire.
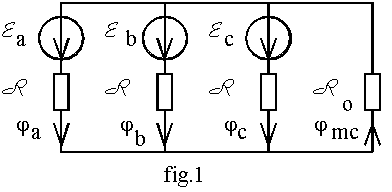
1.2 Modélisation du circuit magnétiqueNous utilisons le modèle ci-contre pour étudier la magnétisation du transformateur.
Pour un noyau bobiné, R est la réluctance et la f.m.m. est E = S ei.ni.ji avec ei = 1 si le courant ji entre par le point repérant le sens de bobinage et ei = -1 dans le cas contraire; la somme est étendue à tous les courants des bobinages portés par la colonne étudiée.
Ro est la réluctance du trajet suivi par le flux de mode commun jmc = 3.jo , jo étant la composante homopolaire des flux des colonnes bobinées : jo =( ja + jb + jc ) / 3 .
La réluctance Ro est :
soit celle de la quatrième colonne, sa valeur est alors voisine de R,
soit celle des quatrième et cinquième colonnes en parallèle dans un transformateur cuirassé, elle est alors voisine de R /2 ;
dans le cas d'un transformateur à trois colonnes, elle est mal définie et beaucoup plus élevée.
Les équations du circuit magnétique sont alors :
(1) Ea = R.ja + Ro.jmc ; (2) Eb = R.jb + Ro.jmc ; (3) Ec = R.jc + Ro.jmc ;
pour calculer le flux de mode commun, nous devrons aussi utiliser l'équation globale des ampères-tours obtenue en ajoutant membre à membre les trois équations :
(4) Ea + Eb + Eb = R.(ja +jb +jc ) +3. Ro.jmc = ( R +3. Ro) .jmc .
1.3 Etude des divers couplages
Nous négligeons le courant magnétisant du transformateur et nous appelons: Z = R+j.L.w l'impédance de pertes d'une bobine primaire et Z' = R'+j.L'.w l'impédance de pertes d'une bobine secondaire (R correspond à la résistance de la bobine et L est son inductance de fuites).
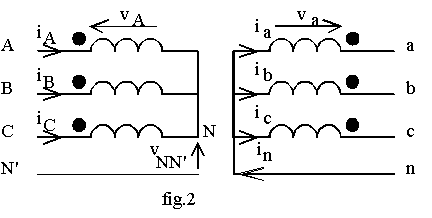
Couplage Yyn
N' est le neutre du réseau et N le neutre du bobinage primaire.
Ecrivons les équations du montage :
Soit v1 , v2 et v3 les tensions simples du réseau primaire supposé équilibré.
(5)V1 = VA+ VNN' ; (6) V2 = VB+ VNN' ; (7) V3 = VC+ VNN'; (8) VA = Z.IA + j.n1.w.Fa
(9) VB = Z.IB + j.n1.w.Fb ; (10) VC = Z.IC + j.n1.w.Fc ;
(11) Va = j.n2.w .Fa - Z'.Ia ; (12) Vb = j.n2.w.Fb - Z'.Ib ; (13) Vc = j.n2.w.Fc - Z'.Ic.
(1) devient n1.IA - n2.Ia =R.Fa + Ro.Fmc ; (2) donne n1.IB - n2.Ib =R.Fb + Ro.Fmc ;
(3) donne n1.IC - n2.Ic =R.Fc + Ro.Fmc;
Le réseau étant supposé équilibré, la somme des tensions simples du réseau est nulle :
V1 +V2 +V3 = 0; en utilisant les équations (5) à (10) il vient:
j.n1.w.( Fa + Fb +Fc ) +3.VNN' = 0 soit : (14) Fmc = 3 VNN' / j.n1.w .
L'équations aux ampères-tours totaux donne
(4) n1.(IA +IB +IC) - n2.(Ia+Ib +Ic ) = (R +3.Ro). Fmc .
Si le transformateur est supposé parfait, le courant magnétisant est nul donc la réluctance R est nulle.
Ø si le neutre primaire est déconnecté du neutre réseau, la somme des courants primaires est nulle donc:
(4) n2.In = (R +3.Ro). Fmc.
La charge secondaire étant déséquilibrée, le courant neutre in est différent de 0 donc il existe un flux homopolaire Fo = Fmc /3 = n2.In / 3.(R +3.Ro) .
De l'équation (14) nous déduisons VNN' = j.n1.w .Fmc / 3 = j.n1.n2.w.In/3.(R +3.Ro) ; l'existence d'une tension entre le neutre réseau et le neutre primaire indique le déséquilibre des tensions simples primaires donc secondaires. Le déséquilibre est d'autant plus grand que Ro est faible; nous avons intérêt à utiliser un transformateur à flux liés, c'est à dire à trois colonnes.
Pour un transformateur parfait, Fmc = n2.In /3.Ro ; (1) donne
n1.IA - n2.Ia = Ro.Fmc = n2.In /3 , soit en posant mc = n2/n1, IA = mc.( Ia + In /3 ).
Dans ce montage la composante homopolaire in/3 des courants secondaires ne peut être compensée par la composante homopolaire primaire nulle; le flux homopolaire qui en résulte déséquilibre les tensions et sature plus le transformateur.
Le couplage Yyn ne peut donc être utilisé en régime déséquilibré
Ø si nous relions le neutre primaire au neutre réseau (couplage YNyn) , nous équilibrons les tensions primaires l'addition des équations (5), (6), (7) donne maintenant avec , VNN' = 0 et IA +IB +IC =IN , jn1.w.Fmc +Z .IN = 0 ; l'équation (4) donne : n1.IN - n2.In = (R +3.Ro).Fmc d'où nous tirons :
IN = j.n1.n2.w .In / [ Z.(R +3Ro) - jn1².w ] .
L'impédance interne Z étant faible, le flux homopolaire est plus faible que précédemment et les tensions secondaires sont quasi équilibrées; mais il apparaît un courant neutre primaire pouvant être de l'ordre des courants dans les fils de phase; généralement le fil neutre n'est pas dimensionné pour un tel courant donc le montage YNyn est peu utilisé. Ici encore nous avons intérêt à avoir un transformateur à flux liés pour augmenter Ro donc diminuer le courant neutre primaire.
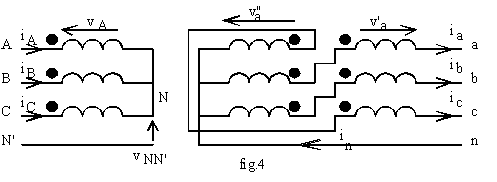
couplage Dyn
La fig.3 donne le schéma de couplage. 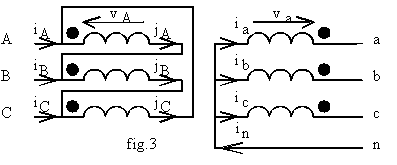
Les équations du montage sont :
(15) U12 = VA = Z.JA + j.n1.w.Fa ; (16) U23 = VB = Z. JB + j.n1.w.Fb;
(17) U31= VC = Z. JC + j.n1.w .Fc ; (1) n1.JA - n2.Ia = R.Fa + Ro.Fmc ;
(3)
n1.JB - n2.Ib = R.Fb + Ro.Fmc; (3) n1.JC - n2.Ic =R.Fc + Ro.Fmc
(18) Va = j.n2.w.Fa - Z'.Ia ; (19) Vb = j.n2.w.Fb - Z'.Ib ; (20) Vc = j.n2.w. Fc - Z'.Ic.
Les tensions par enroulement primaire sont égales aux tensions composées du réseau donc sont équilibrées; la chute de tension dans Z étant faible, les flux sont quasi équilibrés d'après les équations (15), (16), (17) ; d'après les équations (18) à (20) les tensions secondaires restent quasi équilibrées.
Si le transformateur est parfait, Z = 0 donc Fmc = 0 et (1) donne en posant mc = n2/n1,JA = mc. Ia et
IA = JA-JC = mc. (Ia - Ic).
Ce couplage est donc bien adapté au fonctionnement en régime déséquilibré; par rapport au couplage étoile au primaire, la tension par enroulement est Ö3 fois plus forte; pour un même flux par colonne il faudra donc Ö3 fois plus de spires au primaire; pour un réseau primaire haute tension, le bobinage primaire sera coûteux en cuivre et demandera un isolement soigné entre les spires.
Le montage est celui de la fig.4. Les équations de ce montage sont :
(21) V1 = VA+ VNN' ; (22) V2 = VB+ VNN' ; (23) V3 = V3+ VNN'
(24) VA = Z.IA + j.n1.w .Fa ; (25) VB = Z.IB + j.n1.w.Fb ; (26) VC = Z.IC + j.n1.w.Fc
(1) n1.IA + n2.Ia -n2.Ic =R.Fa +Ro.Fmc ; (1) n1.IB+ n2.Ib- n2.Ia =R.Fb +Ro.Fmc ;
(3) n1.IC + n2.Ic- n2.Ib =R.Fc +Ro.Fmc
(27) V'a = -j.n2.w .Fa - Z'.Ia ; (28)V"a = -j.n2.w.Fa + Z'.Ic ; nous en déduisons les tensions par enroulement pour les colonnes b et c par permutation circulaire des indices;
(29) Van = V'a - V"b = j.n2.w.( Fb - Fa ) - 2.Z'.Ia ;
(30) Vbn = V'b - V"c = j.n2.w.( Fc - Fb ) - 2.Z'.Ib
(31) Vcn = V'c - V"a = j.n2.w.( Fa - Fc ) - 2.Z'.Ic ;
L'équation (4) des ampères-tours totaux donne :
n1.IA + n1.IB + n1.IC =R.( Fa+ Fb + Fc ) + 3.Ro.Fmc ; le neutre primaire n'étant pas branché, la somme des courants primaires est nulle d'où: 0 = (R + 3Ro ).Fmc ; le flux homopolaire est nul pour un couplage Yz. En additionnant les équations (21) à (26), nous obtenons pour un réseau équilibré en tension:
V1 +V2 +V3 = Z.(IA +IB +IC )+ j.n1.w.( Fa+ Fb + Fc )+3.VNN' ; soit 0 =0 + 0 +3 VNN' ; nous en déduisons que V1 = VA donc que les tensions primaires sont équilibrées; aux chutes de tensions près, les tensions secondaires restent quasi équilibrées.
En posant mc = n2/n1, n2 étant le nombre de spires par demi enroulement secondaire, IA = mc. (Ic - Ia).
Le couplage Yzn permet donc de garder des flux et des tensions primaires équilibrées; les tensions secondaires sont quasi équilibrées; le fonctionnement est très satisfaisant. L'inconvénient du montage zigzag est de nécessiter 2/Ö3 =1,15 fois plus de spires que le couplage y; la résistance secondaire sera plus forte en raison d'un plus grand nombre de spires et des liaisons entre les demi-enroulements.
En conclusion, nous utilisons:
v le couplage Yyn pour les récepteurs faiblement déséquilibrés
v le couplage Yzn pour les récepteurs fortement déséquilibrés et pour les puissances faibles ou moyennes
v le couplage Dyn pour les récepteurs fortement déséquilibrés et pour les puissances élevées (économie de cuivre par rapport au Zyn).
2.1 Principe
Soit un transformateur monophasé alimenté par un réseau sinusoïdal de fréquence f; le secondaire alimente une charge à travers un redresseur monophasé ou biphasé. Nous considérons que le transformateur est parfait. Dans ce cas, la tension secondaire est v2 = m.v1 , sinusoïdale de fréquence f.
La tension d'alimentation, la structure du redresseur et la charge étant imposées, le courant secondaire j2 est imposé; il est non sinusoïdal et de fréquence égale à celle du le réseau.
Nous pouvons écrire que j2 = J2moy + j2ond , J2moy étant sa valeur moyenne et j2ond son ondulation instantanée. Le courant étant périodique, nous pouvons utiliser sa décomposition en série de Fourier et écrire:
j2ond = S J2km.cos ( 2.k.p.f..t -yk) , somme étendue à k variant de 1 à l'infini.
La composante continue secondaire J2moy crée un flux continu Fo ; ce flux ne peut créer une f.é.m. au primaire ni une intensité primaire. Son seul effet est d'augmenter la saturation du circuit magnétique.
Chaque composante sinusoïdale j2k de fréquence k.f crée un flux de même fréquence et une f.é.m. primaire. D'après la théorie du transformateur en régime sinusoïdal, nous savons que le primaire appelle un courant sinusoïdal j1k = m.j2k pour annuler le flux créé par le secondaire. Nous aurons donc au primaire l'intensité :
j1 = m.S J2km.cos( 2.k.p.f .t -yk) = m. j2ond .
Le flux dans le circuit magnétique est la somme d'une composante sinusoïdale de fréquence f forcée par la tension primaire et correspondant au courant magnétisant à vide et d'une composante continue créée par la composante continue du courant secondaire. Il faut tenir compte de cette composante dans le dimensionnement du transformateur pour ne pas saturer exagérément le circuit magnétique.
Pour les intensités, nous avons:
v au secondaire: valeur moyenne <j2> = J2moy ; valeur efficace J2 =Ö(J2moy² +J2ondeff²)
v
au primaire: valeur moyenne <j1> = 0 ; valeur efficace J1 = m.J2ondeff.
Lorsqu'un transformateur alimente un redresseur, l'intensité secondaire est la somme d'une composante continue J2moy et d'une composante alternative j2ond ; seule la composante alternative crée des ampères-tours primaires; nous aurons donc j1 = m.j2ond en négligeant le courant magnétisant
2.2 Exemple d'un redresseur simple alternance
Le redresseur est formé d'une seule diode en série avec la charge. Supposons que la charge soit une résistance R. Prenons un transformateur 220 / 24 V et une résistance R =12 W. Les graphes théoriques des grandeurs sont données sur la fig.5.
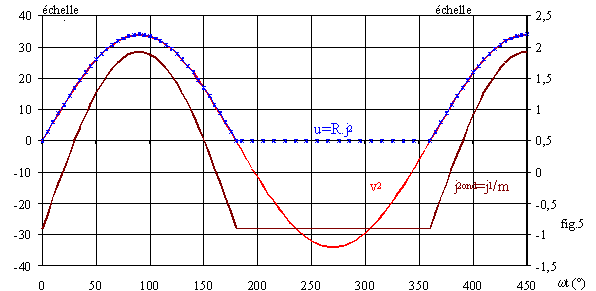
La tension aux bornes de la charge a pour valeur moyenne <u > = Ö2.V2/p et pour valeur efficace
U = V2/Ö2, soit numériquement <u > = 10,8 V et U =17,0 V. Nous avons i = j2 = u/R d'où :
< j2 > = 10,8 / 12 = 0,90 A et J2 =17 /12 = 1,41 A. Nous en déduisons l'ondulation efficace
J2ondeff =Ö(J2² - J2moy²) =1,09 A.
Le rapport de transformation est m = 24 / 220 = 0,109 et l'intensité efficace primaire est :
J1 = m..J2ondeff = 0,119 A.
La puissance active secondaire est P2 = R.J2² = 24 W et la puissance apparente est S2 = V2.J2 =33,9 VA; le facteur de puissance secondaire est Fp2 = P2/S2 = 0,707 .
La puissance active primaire est P1 = P2 =24 W pour un transformateur parfait et la puissance apparente est S1 = V1.J1 =26,2 VA; le facteur de puissance primaire est Fp1 = P1/S1 =0,917 . En ne transmettant pas au primaire la composante continue secondaire, le transformateur améliore le facteur de puissance.
Si nous décomposons j2 en série de Fourier, le terme fondamental du développement est :
j21 = (V2 / R.Ö2 ).sin w.t en phase avec v2 et de valeur efficace J21 égale à 1 A. La puissance réactive secondaire est : Q2 = V2.J21 cos (j21,v2) = 0. La puissance réactive primaire est donc également nulle.
Les puissances déformantes sont : au secondaire D2=Ö(S2²-P2²-Q2²)=23,9 VA et au primaire
D1 =10,5 VA
Si on prend en compte les imperfections du transformateur, les résultats peuvent être notablement différents.
La figure ci-contre donne l'allure des couranst relevés : 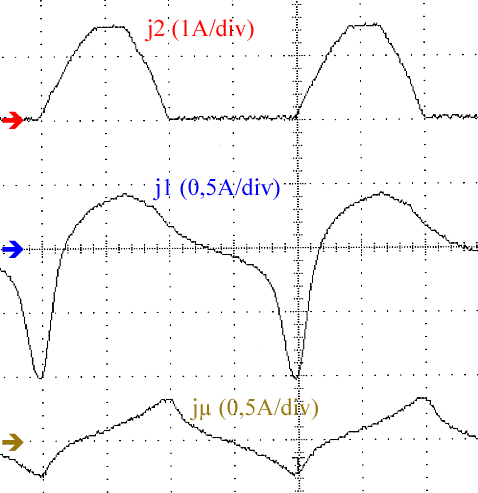
Cette puissance donne un déplacement du facteur de puissance
cosj1 = cos(arctg(Q1/P1) = 0,61 donc la part du facteur de puissance dûe aux harmoniques est
0,46/0,61 = 0,76, valeur inférieure à celle du secondaire.
Le transformateur réduit la puissance déformante ce qui veut dire qu'il réduit les harmoniques injectés dans le réseau. Lors du dimensionnement du transformateur, il faut tenir compte du flux continu pour le calcul de la section du circuit magnétique.
Lorsqu'un transformateur triphasé alimente un redresseur à diodes ou à thyristors débitant sur une charge très inductive, le secondaire du transformateur est parcouru par des courants constants par intervalles de valeur moyenne nulle ou non.
3.1 Principe de l'étude
Nous utilisons le modèle du circuit magnétique représenté sur la fig.1.
Ecrivons les équations de ce circuit:
Ea - R.ja = Ro.jmc ; Eb - R.jb = Ro.jmc ; Ec - R.jc = Ro.jmc ; ja + jb+ jc = j mc .
En ajoutant les relations, il vient : (Ea +Eb +Ec )- R.j mc =3.Ro.j mc . Nous en déduisons:
j mc = (Ea +Eb +Ec ) /(R + 3.Ro ) ; le flux dans le noyau k (k = a , b , c ) est:
jk =[Ek - Ro.(Ea +Eb +Ec )/(R + 3.Ro) ] / R ; Ro / (R + 3.Ro ) =1/3-R/3(R + 3.Ro) il vient alors:
jk =[Ek - (Ea +Eb +Ec ) / 3 ] / R + j mc / 3 .
Nous pouvons négliger la réluctance R d'une colonne bobinée. Nous avons alors:
Ea =Eb =Ec = Ro.jmc; (32) j mc = (Ea +Eb +Ec ) / (3.Ro) ; pour que le flux par colonne bobinée reste fini lorsque R tend vers 0 il est nécessaire que Ek - (Ea +Eb +Ec )/3 tende aussi vers 0; nous aurons donc (33) Ek = (Ea +Eb +Ec ) / 3 .
3.2 Exemple d'un redresseur P3
Le montage du redresseur P3 impose de disposer d'un fil neutre au secondaire; le couplage triangle est donc exclus au secondaire. Prenons un couplage secondaire yn et étudions le fonctionnement en fonction du couplage primaire.
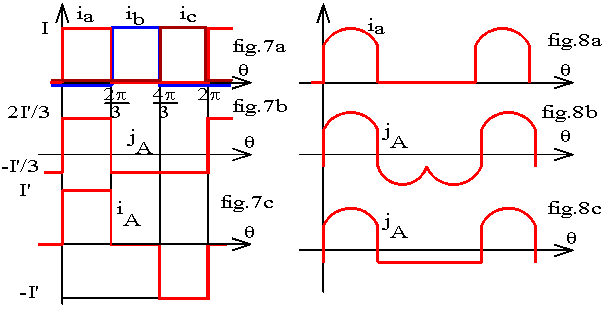
Pour un courant I = Cste, les courants secondaires sont représentés sur la fig.7a. Le courant par phase secondaire a pour valeur moyenne < j2 > = I / 3.
Nous appelons mc le rapport de transformation par colonne n2/n1 et i' = mc.i le courant charge ramené au primaire.
La f.m.m. de la colonne A est Ea = n1.jA - n2.ia = n1.( jA - mc.ia ) ; l'équation (33) donne avec k = a :
jA-mc.ia =(jA+jB+jC)/3-mc.(ia+ib+ic)/3 ; ia+ ib + ic = I d'où: jA = mc.ia + ( jA + jB + jC) / 3 - mc.I /3 .
Le montage du redresseur P3 impose de disposer d'un fil neutre au secondaire; le couplage triangle est donc exclus au secondaire. Prenons un couplage secondaire yn et étudions le fonctionnement en fonction du couplage primaire.
Pour un courant I = Cste, les courants secondaires sont représentés sur la fig.7a.
Le courant par phase secondaire a pour valeur moyenne < j2 > = I / 3.
Nous appelons mc le rapport de transformation par colonne n2/n1 et i' = mc.i le courant charge ramené au primaire.
La f.m.m. de la colonne A est
Ea = n1.jA - n2.ia = n1.( jA - mc.ia ) ; l'équation (33) donne avec k = a :
jA-mc.ia =(jA+jB+jC)/3-mc.(ia+ib+ic)/3 ; ia+ ib + ic = I d'où: jA = mc.ia + ( jA + jB + jC) / 3 - mc.I /3 .
La composante continue du courant secondaire n'est pas transmise au primaire.
Le courant en ligne primaire, égal au courant par phase est représenté sur la fig.7b.
La f.m.m par colonne est Ea = -n1.mc .I /3 = -n2.I/ 3 ; l'équation (32) donne le flux jmc :
jmc = (Ea +Eb +Ec )/ 3.Ro soit jmc = -n2.I / 3. Ro ; ce flux continu passe dans la colonne sans bobinage du transformateur cuirassé ou dans l'air et la cuve du transformateur à flux liés; un flux continu égal à jmc/3 passe dans chaque colonne bobiné créant une pré-aimantation des noyaux risquant de les saturer.
Lorsque le courant de la charge n'est pas parfaitement lissé, les équations obtenues restent valables;
l'allure des courants est alors donnée par la fig.8a, b. Le flux jmc a alors en plus une composante alternative
de fréquence 3 f, f étant la fréquence du réseau primaire. Cette composante induit d'importantes pertes dans le fer.
Le montage Yyn ne convient donc pas à cet usage.
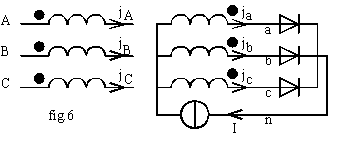
couplage Dyn
En négligeant les impédances internes, la tension entre phases réseau, égale à la tension par enroulement primaire, est égale à la f.é.m : ujk = n1.djk /dt ; la somme des tensions en ligne réseau étant nulle,
il vient d(ja + jb+ jc )dt = 0 ; nous en déduisons que le flux jmc a une dérivée nulle donc est constant quelle que soit la forme des courants.
Dans le couplage Dyn la composante variable du flux commun est court-circuitée.
De l'équation (32), nous tirons jmc = [n1.(jA + jB +jC ) - n2.(ia+ ib + ic) ]/ 3.Ro ; jmc étant indépendant du temps et les relations pour les trois colonnes étant identiques, nous en déduisons que n1.jA = n2.ia+K , avec K = Cste indépendante du temps.
Calculons la valeur moyenne sur une période de cette expression: < jA > = mc.< ia > + K/ n1 . Les composantes continues ne peuvent être transmises par le transformateur donc jA est alternatif et sa valeur moyenne est nulle.
Chaque diode conduisant tout le courant pendant 1/3 de période, la valeur moyenne du courant secondaire est le tiers de la valeur moyenne du courant charge; il vient donc : 0 = mc.<i > / 3 + K /n1 ; nous obtenons finalement jA = mc.( ia - < i >/ 3).
Le courant en ligne se calcule par iA = jA - jC. Les graphes de jA et de iA sont donnés par la fig.7b et 7c pour i = I = Cste ; pour un courant ondulé le courant par phase est représenté sur la fig.8.c.
De l'équation (32) nous tirons jmc = - n2.< i > /3.Ro ; ce flux continu se répartit en jmc /3 dans chaque noyau, provoquant une pré-aimantation du circuit magnétique dont il faut tenir compte dans le dimensionnement des noyaux.
Le couplage Dyn a l'avantage de ne pas introduire de pertes supplémentaires dues à l'ondulation du courant de charge; l'existence d'un flux homopolaire continu limite son emploi à des puissances ne dépassant pas 20 kW; au delà des ces puissances, il faudrait choisir un couplage zigzag au secondaire ; celui-ci en répartissant
le courant d'une phase sur deux colonnes annule la composante continue des flux.
On utilise rarement le redresseur P3 pour de telles puissances; on lui préfère alors le PD3 qui n'introduit pas de composante continue dans les courants secondaires.
Dans les montages de commande, on peut utiliser un transformateur pour transmettre un signal
de commande à un interrupteur avec isolement entre la commande et la puissance.
Ce signal est le plus souvent un signal en créneaux positifs.
4.1 Modèle utilisé
On utilise un modèle simplifié :
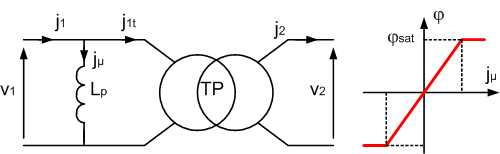
on néglige :
les pertes magnétiques et les pertes par effet Joule
les fuites magnétiques
les capacités parasites
l'hystérésis du matériau magnétique
On suppose que la matériau est linéaire pour des valeurs du courant magnétisant -jsat < jµ < jsat et
que lorsque le matériau est saturé ( |jµ| > jsat) j = jsat = Cste .
Le transformateur parfait TP possède n1 spires au primaire et n2 = m.n1 spires au secondaire; il impose
v2 = m.v1 et j1t = m.j2 .
L'inductance magnétisante Lp est constante en régime linéaire et nulle en régime saturé.
v1 = n1.dj /dt et n1.j = Lp.jµ.
4.2 Réponse à une impulsion
On étudie le montage ci-dessous :
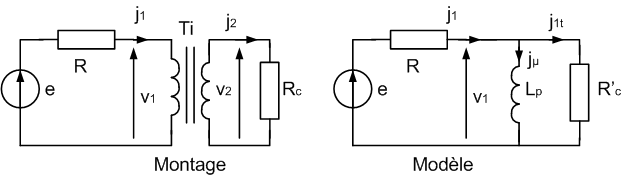
R'c est la résistance de charge ramenée au primaire : TP + Rc équivaut à R'c = Rc / m².
On applique un créneau de tension, en supposant que le flux dans le transformateur est initialement nul.
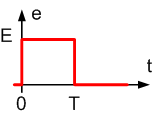
Les équations du circuit sont : v1 = e - R.j1 = Lp.djµ/dt , j1t = v1/R'c et j1 = jµ + j1t
Calcul simplifié
Supposons le générateur d'entrée parfait soit R = 0.
Pour t > 0 djµ /dt = v1/Lp = E/Lp = Cste donc jµ = E.t/Lp + A
Comme le flux est initialement nul, jµ = n1.j /Lp = 0 en t = 0 donc A = 0.
j1t = E/R'c et j1 = E.(t/Lp + 1/R'c) .
En t = T, on a jµmax = E.T / Lp. Deux cas sont alors à envisager :
è jµmax < jsat : dans ce cas, le transformateur ne se sature pas durant l'impulsion et Lp reste constante
è jµmax > jsat : dans ce cas, le transformateur se sature en un instant t1 < T. Lp devient alors nulle
et la source est court-circuitée par le transformateur. Le courant magnétisant n' est plus limité que
par la résistance du bobinage que l'on a négligé. Ce fonctionnement ne peut être autorisé.
Pour un fonctionnement correct, nous devons avoir E.T /Lp < jsat. Pour un transformateur donné , Lp
et jsat sont fixés, la condition devient E.T < Lp.jsat , quantité appelée "produit Et " du transformateur .
E.T représente la surface de l'impulsion; c'est cette quantité qui doit être limitée pour un
bon fonctionnement. Par exemple pour un transformateur de produit Et = 100 V.µs, on peut transmettre
une impulsion de 10 V durant moins de 10 µs ou une impulsion de 5 V durant moins de 20 µs.
Supposons que le transformateur ne se sature pas durant l'impulsion et envisageons ce qui se passe pour
t > T. On a alors e = v1 = 0 soit djµ /dt = 0 donc jµ = Cste = jµmax. Le transformateur reste donc magnétisé.
On a j1t = 0 et j1 = jµmax.
La figure ci-dessous donne l'allure des grandeurs:
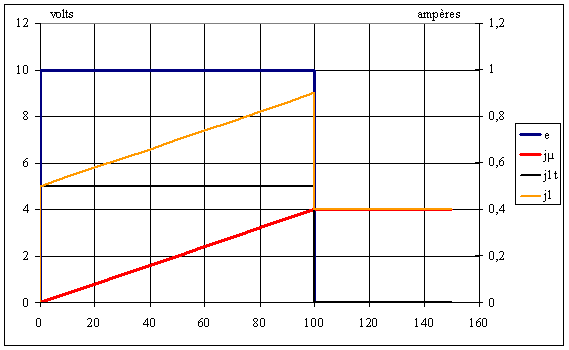
Influence de la résistance de la source
Tenons compte de la résistance R de la source :

La figure ci-dessous donne l'allure des graphes :
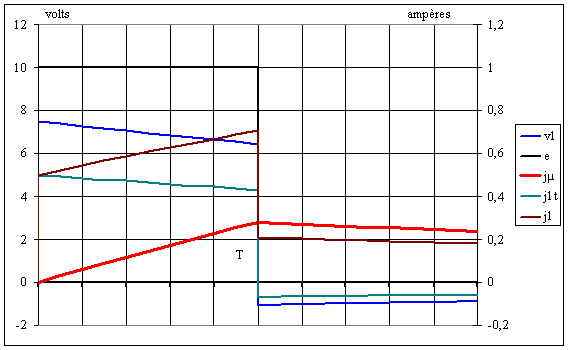
Nous constatons que la résistance de la source a :
è des effets favorables :
en réduisant le courant magnétisant, elle permet de transmettre une impulsion de surface plus grande
en permettant une lente démagnétisation pour t > T
è des effets défavorables :
en déformant et réduisant la tension v2 = m.v1 appliquée à la charge
en augmentant les pertes
4.3 Réponse à un créneau de tension
On applique maintenant une tension e ayant la forme d'une tension en créneau positif d'amplitude E,
de période T et de rapport cyclique a.
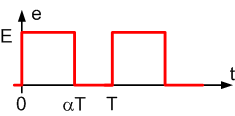
Le transformateur est initialement démagnétisé. De 0 à a.T, on a le fonctionnement étudié ci-dessus:

et ainsi de suite.
La figure ci-dessous donne l'allure des grandeurs :
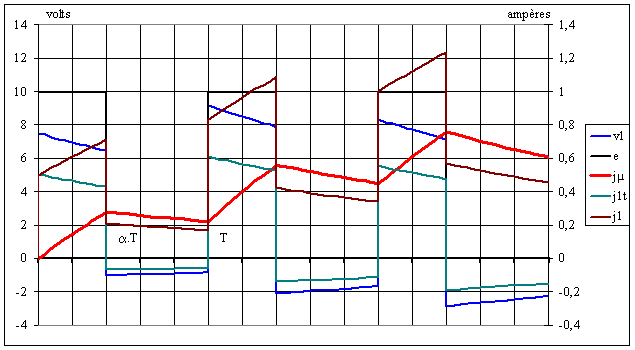
On constate que ce montage ne fonctionne pas correctement :
è le transformateur ne se démagnétise pas donc le courant magnétisant croît constamment; on arrivera
donc à la saturation du transformateur après quelques périodes
è la tension secondaire est déformée, la composant continue de la commande n'est pas transmise
Pour que le montage fonctionne correctement, il faut démagnétiser le transformateur à chaque période.
Pour faire décroître rapidement le courant magnétisant, il faut appliquer une tension négative au primaire.