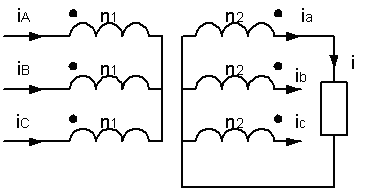
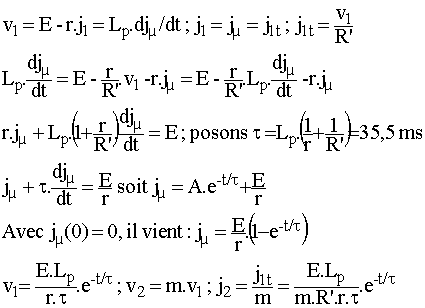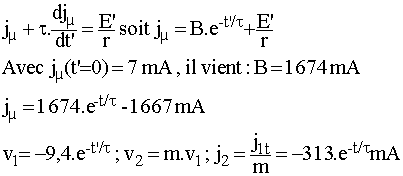Un transformateur triphasé parfait 10kV / 400 V de couplage Yyn alimente entre la phase a et le neutre n une résistance R = 100 W
|
Calculer le rapport mc des nombres de spires des enroulements primaire et secondaire |
mc = Va/VA = Uab/UAB = 0,04
Réponse |
| Calculer les courants efficaces au secondaire |
Va = 231 V
Ia = In = 2,31 A ; Ib = Ic = 0
Réponse |
| Exprimer le flux de mode commun |
Écrire les équations aux ampères-tours des trois phases puis globaliser les At
Aide |
n1.iA - n2.ia = R.ja + Rc.jmc = Rc.jmc car R = 0 pour un transformateur parfait
n1.iB - n2.ib = Rc.jmc ; n1.iC - n2.ic = Rc.jmc
n1.(iA+iB+iC) - n2.(ia+ib+ic) = 3 Rc.jmc
jmc = -n2.ia /3.Rc
Réponse |
| Calculer les intensités efficaces au primaire |
n1.iA = n2.ia +Rc.jmc =2.n2.ia /3 ; iA = 2. mc.ia /3 ; IA = 62 mA
iB = iC = -mc.ia /3 ; IB = IC= 31 mA
Réponse |
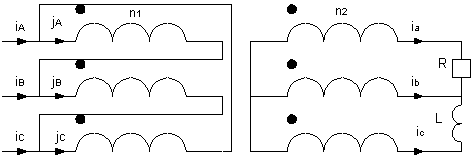
Un transformateur triphasé parfait 1kV / 400 V de couplage Dy alimente entre la phase a et le neutre b une résistance R = 100 W et entre la phase b et la phase c une inductance de réactance X=Lw= 200 W
|
| Calculer le rapport mc = n2/n1 |
mc = Va/VA = (Uab/Ö3)/UAB = 0,231
Réponse |
| On suppose le réseau équilibré direct et on prend comme origine des phases la tension UAB; donner le module et l'argument des tensions composées primaires et secondaires |
Pour trouver l'argument des tensions secondaires, déterminer l'indice horaire
Aide |
UAB = (1000 ; 0°) ; UBC = (1000 ;-120°) ; UCA = (1000 ; 120°)
Indice horaire 5 donc (uab,UAB) = 150°
Uab = (400 ; -150°) ; Ubc = (400 ;-270°) ; yca = (400 ; -30°)
Réponse |
| Calculer le module et l'argument des intensités secondaires |
Ia =Uab /R = (4 ; -150°) ; Ic =Ubc /jX = (2 ; -180°) ; Ib =-Ia -Ic = (5,82 ; 20°)
Réponse |
| Montrer que le flux de mode commun est nul |
Les f.é.m. primaires sont imposées par le réseau ( eA = -uAB) donc sont équilibrées
EA = -j.n1.w.Fa donc les flux sont équilibrés et
jmc = ja + jb + jc = 0
Réponse |
| Calculer le module et l'argument des courants dans les enroulements primaires |
Écrire les équations aux ampères-tours avec R = 0 pour un transformateur parfait et jmc = 0
Aide |
n1.jA + n2.ia= 0 donc JA =- mc.Ia= ( 0,92 ; 30°)
JB =- mc.Ib= ( 1,34 ; 200°)
JC =- mc.Ic= ( 0,46 ; 0°)
Réponse |
| Calculer le module et l'argument des courants en ligne au primaire |
IA = JA - JC = (0,57 ; 54°)
IB = JB - JA = (2,25 ; -156°)
IC = JC - JB = (1,79 ; 15°)
Réponse |
Calculer les puissances active et réactive fournies au primaire
|
Calculer les puissances consommées par chaque impédance de charge
Aide |
R consomme Pr = Uab²/R = 1,6 kW et Qr = 0
L consomme PL = 0 et QL = Ubc²/X = 0,8 kVAR
Le transformateur est parfait donc sans pertes
P = 1,6 kW et Q = 0,8 kVAR
Réponse |
| Quelle méthode doit-on utiliser pour mesurer la puissance active au primaire et quelles sont les lectures des wattmètres utilisés |
Un wattmètre branché en série dans la ligne n° i et en tension entre les lignes j et k mesure
Ujk.Ii.cos[argUjk - arg Ii]
Aide |
La méthode des deux wattmètres
PAAC = UAC.IA.cos(120+180-54)=-231 W
PBBC = UBC.IB.cos[-120-(-156)]=1831 W
Réponse
|
| Quelle méthode doit-on utiliser pour mesurer la puissance réactive au primaire et quelles sont les lectures des wattmètres utilisés |
La méthode des deux wattmètres n'est pas utilisable en régime déséquilibré
Aide |
Q = (PABC + PBCA+PCAB)/Ö3
Q = (-569 + 231 + 1724)/Ö3 = 800 VAR
Réponse |
Un transformateur monophasé parfait alimenté sous V1 = 230 V débite sur une charge non linéaire; on a relevé au secondaire les grandeurs de la figure ci-dessous :

|
| Calculer la valeur efficace de la tension secondaire et le rapport de transformation |
V2max = 68 V . V2 = V2max / Ö2 =48 V
m = 48 / 230 = 0,209
Réponse |
| Calculer les valeurs moyennes et efficaces du courant secondaire. Calculer l'ondulation efficace de ce courant |
J2moy = 10 * 120/360 = 3,33 A
J2eff = 10Ö(120/360) = 5,77 A
J2ondeff =Ö(J2eff² -J2moy²) = 4,71 A
Réponse |
| Calculer le terme fondamental de la série de Fourier de j2 |
|
| Calculer les puissances active, réactive, apparente, déformantes et le facteur de puissance au secondaire |
P et Q sont créées uniquement par le fondamental de j2
P2 = V2.J21.cos0 = 187 W ; Q2 = V2.J21.sin0 = 0
S2 = V2.J2 = 277 VA ; D2 =Ö(S2² -P2²-Q2²) = 205 VA
Fp2 = P2/S2 = 0,475
Réponse |
| Calculer l'intensité efficace au primaire |
La composante continue n'est pas transmise donc
J1 = mc . Jondeff = 0,98 A
Réponse |
| Calculer les puissances active, réactive, apparente, déformantes et le facteur de puissance au primaire |
Le transformateur n'a pas de pertes donc
P1 = P2 = 187 W ; Q1 = Q2 = 0
S1 = V1. J1 = 226 VA
D1 = 127 VA ; FP1 = P1 / S1 = 0,827
Réponse |
| Y-a-t-il une composante continue du flux ? |
n1.j1 + n2.j2 = R.j
En valeurs moyennes
n1.J1moy + n2.J2moy = R. jmoy
comme J1moy = 0 et J2moy = 3,33 A, il y a une composante continue pour le flux
Réponse |
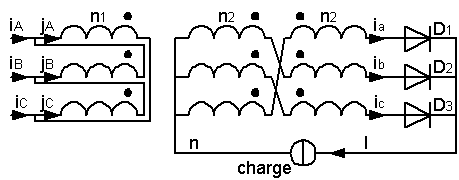
Un transformateur triphasé parfait 5,2 kV / 230 V de couplage Dzn alimente un redresseur parfait de structure P3. La charge absorbe un courant parfaitement lissé I = 30 A
|
| Calculer le rapport mc = n2/n1 |
mc = Ea/EA = (Uab/3)/UAB = 0,015
Réponse |
| Représenter les tensions secondaires phase - neutre, la tension u aux bornes de la charges, les intensités en ligne secondaire |
D1 conduit seule quand Va > Vb et Va > Vc
Aide |
|
| Calculer les valeurs moyennes et efficaces du courant secondaire. Calculer l'ondulation efficace de ce courant |
J2moy = 30 /3 = 10 A
J2eff = 30/Ö3= 17,3 A
J2ondeff =Ö(J2eff² -J2moy²) = 14,1 A
Réponse |
| Montrer que le flux de mode commun est nul |
-n1.jA - n2.ib + n2.ia = Rc.jmc
-n1.jB - n2.ic + n2.ib = Rc.jmc
-n1.jC - n2.ia + n2.ia = Rc.jmc
Globalisation :
-n1.(jA+jB+jC)=3. Rc.jmc
Le flux de mode commun n'a pas de composante continue puisque les courants primaires sont alternatifs
Il n'y a pas non plus de flux de mode commun alternatif puisque le couplage D au primaire impose des tensions donc des flux équilibrés
Réponse |
| Exprimer les courants par enroulement et en ligne au primaire en fonction des courants secondaires |
jA = mc.(ia - ib) ; jB = mc.(ib - ic) ;
jA = mc.(ic - ia) ;
iA = jA - jB = mc.(ia-2.ib+ic)
Réponse |
| Tracer les graphes des courants primaires jA et iA. Calculer leurs valeurs moyennes et efficaces |
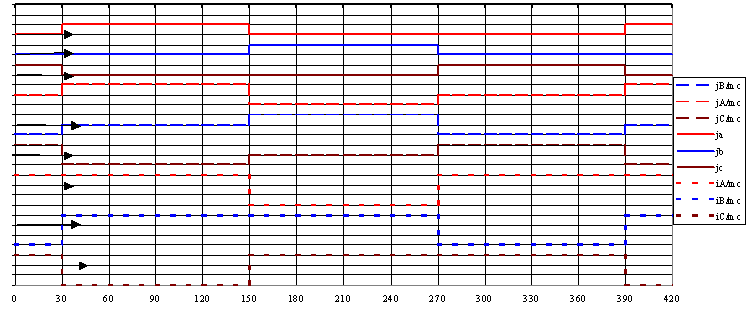
jA vaut mc.I = 0,44 A durant 120° , 0 durant 120° et -mc.I durant 120 ° donc JAmoy = 0 et JAeff = 0,44.Ö(2/3)=0,36 A
iA vaut mc.I durant 2T/3 et -2.mc.I durant T/3 donc IAmoy = 0 et IAeff = mc.I = 0,44 A
Réponse |
On étudie un transformateur d'impulsion de rapport m = 1/3. On donne :
produit "Et" = 2 000 V.µs inductance magnétisante Lp = 200 mH |
| Le transformateur est alimenté par un générateur de tension parfait et la résistance de charge est R = 10 W |
On veut transmettre une impulsion de durée 50 µs ; quelle est l'amplitude
E maximale de l'impulsion ? |
Réponse |
On applique une impulsion d'amplitude E = 15 V et de durée T = 50 µs;
calculer le courant magnétisant, le courant primaire et le courant secondaire |
Aide |
Réponse |
Représenter les graphes de la tension et du courant au primaire et
au secondaire. |
Réponse |
On étudie le montage ci-dessous :
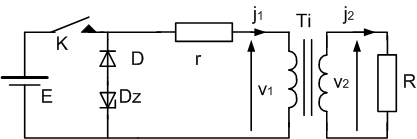
E = 15 V , r = 6 W
D est une diode de tension de seuil Vd = 0,7 V et Dz une diode zéner de tension Vz = 9,3 V
Pour t < 0, K est ouvert et le transformateur est démagnétisé |
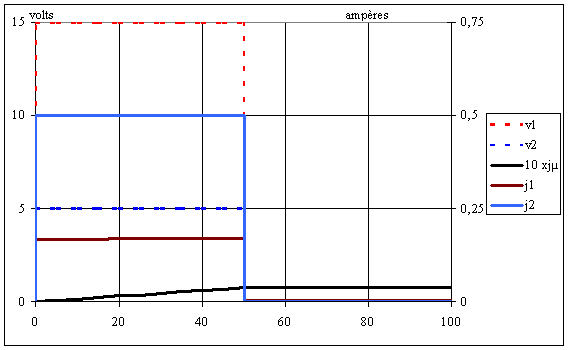
A t = 0, on ferme K durant T = 100 µs. Calculer le courant magnétisant,
les tensions et les courants au primaire et au secondaire. |
Aide |
Réponse |
On pose t' = t - T; on ouvre K en t' = 0 durant un temps T'.
Calculer le courant magnétisant, les tensions et les courants au primaire et au secondaire. |
Aide |
Réponse |
Calculer la valeur minimale de T' qui permet la démagnétisation complète
|
Réponse |
| Que se passet-il si on ferme de nouveau K en t = 250 µs ? |
Réponse |
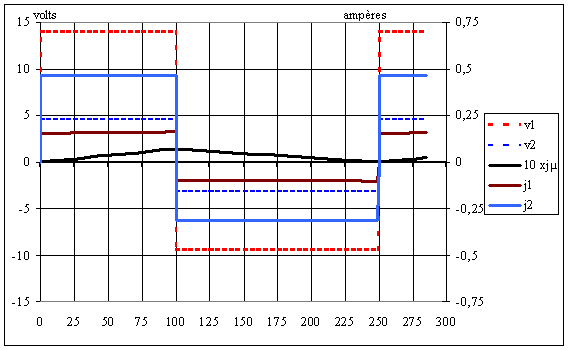
Représenter les graphes de jµ, v1, j1, v2 et j2 si on périodiquement,
on ferme K pendant 100 µs et on l'ouvre pendant 150 µs |
Réponse |