Sur la fig.1.b, nous schématisons le transformateur vu de dessus; le flux dans chaque colonne est forcé par

la tension primaire de la phase correspondante; en régime sinusoïdal, à la pulsation w, il vient:

phase a : v_a = -n₁.dj_a /dt soit en notation complexe F_a = -V_a / j.n₁.w; phase b : F_b = -V_b/ j.n₁.w;

phase c : F_c= -V_c / j.n₁.w; le flux dans la colonne centrale est F_mc = F_a +F_b +F_c

soit F_mc = - (V_a +V_b +V_c) / j.n_1.w; la somme des tensions est égale à trois fois la composante homopolaire

du système des tensions : F_mc = - 3.V_o / j.n₁.w; en régime équilibré de tension cette composante est nulle

donc le flux dans la colonne centrale est nul. Cette quatrième colonne peut être supprimée.

Nous arrivons à la constitution pratique en ramenant les colonnes dans un même plan pour réduire

l'encombrement.

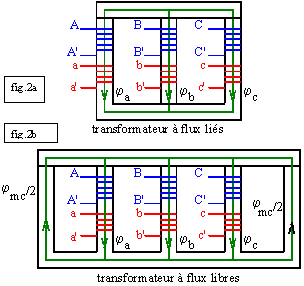
Dans le schéma de la fig.2.a, la colonne commune est supprimée; le flux de mode commun F_mc, somme

des flux des trois colonnes ne peut circuler dans le circuit magnétique; en régime déséquilibré ce flux peut

être différent de 0; il circule alors dans un circuit mal défini empruntant l'air environnant et la cuve du

transformateur lorsqu'elle existe. Ce type est le plus fréquemment utilisé; il sera dit "à flux liés".

La dissymétrie des circuits magnétiques des trois phases donnera des courants magnétisants différents donc

un léger déséquilibre des courants à vide.

Dans le schéma de la fig.2.b, le transformateur est de type cuirassé. La présence des deux colonnes latérales

non bobinées permet de faire circuler le flux de mode commun dans les colonnes latérales de faible

réluctance; pour cela, ce type sera dit "à flux libres".   

En régime triphasé équilibré, tous les types de transformateurs ont le même fonctionnement; en régime

déséquilibré ou dans le fonctionnement en alimentation  d'un commutateur de courant, la possibilité de

faire circuler le flux de mode commun dans le circuit magnétique modifiera le fonctionnement.

2 couplage des enroulements

2.1 Couplage de trois enroulements

Le primaire et le secondaire du transformateur triphasé comportent chacun trois phases à coupler pour

être reliés à des lignes trois ou quatre fils.

Le couplage des enroulements doit respecter les bornes homologues: l'entrée des trois phases doit se faire

du côté du point repérant le sens de bobinage ou du côté opposé au point.

Soit j le flux à travers une spire, la f.é.m. induite dans la spire, orientée dans le sens du courant est 

e = - dj/ dt; pour un enroulement de n spires, la tension est v = ± n.e, + si la tension est orientée à partir

du point repérant le sens d'enroulement, - si la tension est orientée vers le point.

La tension par enroulement, égale à la tension par phase est v = -n.e. La tension composée en ligne a

pour valeur efficace U = Ö3 V. Les intensités en ligne et par enroulement sont égales : i = j.

couplage triangle

La sortie d'un enroulement est relié à l'entrée d'un autre enroulement. Nous avons deux façons de faire le

couplage : numérotons les phases A B C A B C ... nous pouvons relier la sortie de A à l'entrée de B en

progressant vers la droite dans la numérotation, puis B à C et C à A, nous dirons que nous faisons un

triangle à droite. Nous pouvons aussi  relier la sortie de A à l'entrée de C en progressant vers la gauche

dans la numérotation, puis B à A et C à B, nous dirons que nous faisons un triangle à gauche .

La tension par enroulement v = - n.e est égale en valeur efficace à la tension en ligne U.

Pour les courants, il vient : I = Ö3.J.

couplage zig-zag

Chaque colonne porte deux enroulements de n spires. Nous avons v' = v" = n.e.

Chaque phase est formée en reliant les bornes homologues de deux enroulements situés sur deux

colonnes différentes. Nous pouvons faire un zigzag à droite comme sur la figure (colonne A vers

colonne B) ou à gauche (colonne A vers colonne C).

Les trois phases ainsi constituées sont ensuite couplées en étoile.

La tension phase neutre v_n est la différence de deux tensions v' et v" de même valeur efficace et déphasées

de ± 2.p/3 ; en valeur efficace , il vient : V_n = Ö3.V' = Ö3.n.E. Le couplage étant ensuite de type étoile,

nous avons U = Ö3.V_n = 3 .n.E. Pour les intensités I = J.

2.2 Couplage du transformateur

Au lieu de distinguer primaire et secondaire, nous distinguons les enroulements haute tension (HT) et les

enroulements basse tension (BT). Les notations des enroulements HT se font avec des lettres majuscules

et ceux des enroulements BT par une lettre minuscule.

Les bornes des bobines d'une même colonne sont désignées par une même lettre : AA' pour une bobine HT;

aa' ou a₁a'₁, a₂a'₂ pour des bobines BT.

Les modes de couplage de trois enroulements HT ou BT sont désignés par les lettres Y, y pour le couplage

étoile, D, d pour le couplage triangle, Z, z pour le couplage zigzag (majuscule pour HT, minuscule pour BT).

Dans les couplages étoile et zigzag nous ajoutons la lettre N ou n si le point neutre est accessible.

Nous désignerons le couplage du transformateur par les lettres du couplage HT suivi les lettres du couplage

BT : Y_N y_n , D y , Y z_n ...

3 Indice horaire du transformateur

3.1 Définition

Pour un transformateur monophasé les tensions au primaire et au secondaire ne peuvent être déphasées que

de 0 ou 180° suivant les sens d'enroulement; pour un transformateur triphasé alimenté par un réseau équilibré, le déphasage des tensions en ligne HT et BT peuvent prendre toutes les valeurs multiples de 30°. Un angle de 30° représentant l'écart entre deux chiffres consécutifs sur le cadran d'une horloge, ce

déphasage sera dit d'une heure. 

Soit q =(u_ab , u_AB) le déphasage, compté dans le sens trigonométrique direct, de la tension composée HT

par rapport à la tension BT; nous appelons indice horaire du transformateur le nombre

I_h= q (en degrés) / 30.

3.2 Détermination théorique de l'indice horaire

Nous devons représenter sur un diagramme de Fresnel les tensions u_ab et u_AB pour déterminer leur

déphasage.

Connaissant le schéma de couplage du transformateur, nous pouvons déterminer son indice horaire. Pour cela:

v     nous portons sur le schéma les f.é.m des enroulements; par convention, ces f.é.m doivent orientées positivement en partant du point repérant le sens de bobinage.

v     Tous les spires des enroulements d'une même colonne sont traversées par le même flux; leurs f.é.m. sont donc en phase. Pour deux colonnes adjacentes, les flux donc les f.é.m sont déphasées de 120°. Nous traçons donc le système triphasé équilibré direct des f.é.m e_A, e_B et e_C des enroulements HT et en phase, celui des f.é.m. e_a, e_b et e_c des enroulements BT.

v     En utilisant la loi des mailles, nous exprimons les tensions u_AB et u_ab en fonction de ces f.é.m. et nous construisons les vecteurs de Fresnel correspondants.

v     Nous lisons dans le sens trigonométrique positif l'angle (u_ab , u_AB) et nous en déduisons l'indice horaire

Exemple

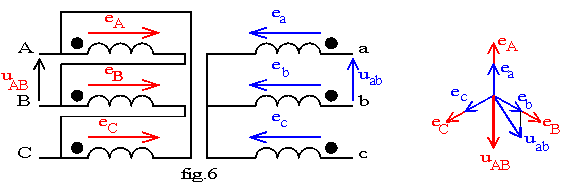
Soit le transformateur schématisé sur la fig.6 .

Nous traçons les f.é.m.; nous en déduisons les tension composées u_ab = e_b - e_a. et u_AB = -e_A .

q = (u_ab , u_AB) = 330 ° donne un indice horaire de 11. Nous dirons que nous avons un transformateur Dy11.                                                                                                                     

3.3 Groupe de couplage

Pour représenter l'indice horaire, nous pouvons sur le cadran d'une horloge placer A à midi, B à 4 h et C à 8h.

Dans ce cas, a est sur l'heure indiquant l'indice horaire, b 4 h plus tard et c 8 h plus tard.

Si nous permutons de façon cyclique les phases d'un enroulement, nous déplaçons de 4 h le point de ligne;

par exemple avec l'ordre BT abc et l'indice 11, a  est à 11 h, b à 3 h et c à 7 h; pour la permutation cab,

a prend la place de b à 3 h et l'indice devient 3; pour la permutation bca a prend la place de c à 7 h

et l'indice devient 7.

Trois indices différents de ±4 peuvent être obtenus pour un même couplage par simple permutation des phases.

Ces indices sont regroupés dans un groupe de couplage. 

Les groupes de couplage sont:

v     groupe I rassemblant les indices  : 0, 4, 8

v     groupe II rassemblant les indices : 2, 6, 10

v     groupe III rassemblant les indices   :  1, 5, 9

v     groupe IV rassemblant les indices  :   3, 7, 11.

Si nous inversons les sens d'enroulement d'un des bobinages HT ou BT, les tensions correspondantes sont déphasées de 180° donc de 6 h; l'indice augmente donc de 6. Nous passons du groupe I au groupe II ou du groupe III au groupe IV en inversant les bobines HT ou BT, sans modifier le couplage.

Notons que seuls les couplages étoile - triangle et étoile - zigzag peuvent donner des indices impairs donc des couplages dans les groupes III et IV.     

3.4 Détermination expérimentale de l'indice horaire

Méthode impulsionnelle

A l'aide d'une pile ou d'une batterie et d'un interrupteur, nous appliquons une brève impulsion de tension continue positive entre les bornes BT a et b. Avec un voltmètre continu polarisé, nous relevons à chaque fermeture de l'interrupteur, le signe de la tension créée entre les bornes AB puis BC puis CA.

La loi de Lenz implique que la tension induite entre A et B est proportionnelle à la projection du vecteur de Fresnel associé en régime sinusoïdal à u_AB sur le vecteur de Fresnel associé à la tension u_ab.

On trace un cadran d'horloge de centre O, gradué en heures; on place A à midi donc B à 4 h et C à 8 h; a est à l'heure indiquée par l'indice horaire. On trace la direction Oa et on projette sur Oa, A en H , B en K et C en L; on note alors les signes des mesures algébriques de OH, OK et OL.

Sur la fig.9a le transformateur est d'indice 0 donc a est placé à 12 h ; OH est positif, OK et OL sont négatifs; la combinaison + - - correspond donc à l'indice 0. Sur la fig.9b, le transformateur a un indice 5; OH est négatif, OK positif, et OL nul; la combinaison - + 0 correspond donc à l'indice 5. On peut ainsi dresser le tableau ci-dessous donnant les combinaisons pour les douze indices:

Cette méthode a l'avantage de la simplicité de mise en œuvre; elle ne nécessite pas une alimentation triphasée adaptée au transformateur. Son inconvénient réside dans l'interprétation difficile des résultats si nous ne disposons pas du tableau ci-dessus.

méthode des électriciens

Nous relions les points A et a pour imposer une référence de tension commune aux bobinages HT et BT; le bobinage HT est alimenté par un réseau triphasé équilibré direct. La mesure des tensions AB, BC, CA permet de construire le triangle ABC des tensions HT et son centre de gravité N, en plaçant A à 12 h . Nous mesurons les tensions Ab, Bb, Cb, Ac, Bc et Cc.

Le point a est confondu avec A; pour trouver le point b, nous traçons les cercles de centre A et de rayon Ab, de centre B et de rayon Bb, de centre C et de rayon Cb; l'intersection de ces cercles donne b. De même l'intersection des cercles de centre A et de rayon Ac, de centre B et de rayon Bc, de centre C et de rayon Cc donne le point c.

Soit n le centre de gravité du triangle abc, la direction na indique sur l'horloge l'heure de couplage.

Par exemple nous obtenons les graphes: fig10.a pour un indice 1 et fig.10.b pour un indice 5.

Cette méthode a l'avantage d'une interprétation simple mais ne peut être appliquée qu'aux transformateurs possédant des bobinages HT et BT isolés; elle ne peut être appliquée à un auto-transformateur car la liaison Aa court-circuiterait une partie du bobinage.

4 rapport de transformation

Le rapport de transformation m est défini comme le rapport des tensions  efficaces en ligne secondaire et  primaire à vide : m = U₂₀ / U₁₀

Ce rapport de transformation dépend des nombres de spires des bobinages et des couplages du primaire et du secondaire.

Pour deux enroulements sur une même colonne, au primaire de n₁ spires et au secondaire de n₂ spires, le rapport des tensions efficaces aux bornes de ces enroulements est m_c = E₂ / E₁ = w.F.n₂ / w.F.n₁ = n₂ / n₁.

Pour un couplage Y, la tension d'enroulement est la tension simple U = V.Ö3 = E.Ö3  ; pour un couplage triangle, cette tension est la tension en ligne : U = V = E. Pour un couplage zigzag de n spires réparties en deux enroulements de n/2 spires, soit E la f.é.m aux bornes des n/2 spires, V =E.Ö3 et U = V.Ö3 =  3.E.

Nous pouvons déduire de m_c le rapport de tension .

En tenant compte du déphasage q = (u_ab,u_AB) = I_h x 30° introduit par le couplage, nous pouvons en régime sinusoïdal, définir le rapport de transformation complexe m = U₂ / U₁ . Ce rapport a pour module m et pour argument ±q, + si le transformateur est élévateur de tension (u₁= u_ab) ,  - si le transformateur est abaisseur de tension (u₁ = u_AB).

5 modèle équivalent en régime équilibrée

Nous étudions le transformateur alimenté au primaire par un réseau triphasé équilibré et chargé au secondaire par un récepteur triphasé équilibré. Nous connaissons le modèle équivalent du transformateur monophasé; en régime équilibré les trois phases fonctionnent avec les mêmes grandeurs efficaces et les mêmes déphasages; nous allons ramener l'étude du transformateur triphasé à celle d'un transformateur monophasé.

5.1 Principe

Modèle du transformateur étoile - étoile : quel que soit le couplage du transformateur Tr étudié, nous définissons un transformateur équivalent Try de couplage Yy0; ce transformateur a des caractéristiques telles que, si nous le substituons au transformateur Tr, les grandeurs en ligne restent identiques tant au primaire qu'au secondaire.

Ce transformateur équivalent peut être modélisé par le modèle monophasé équivalent à une phase.

Ce modèle a l'avantage de convenir à tout type de couplage et de permettre de modéliser simultanément des transformateurs de couplages différents.

L'inconvénient est de ne pas conserver dans le modèle les grandeurs par phase du transformateur Tr et de ne pas conserver les déphasages primaire - secondaire. En effet dans un couplage Yy0 les tensions u₁ et u₂ sont en phase alors que dans le transformateur Tr, (u_ab,u_AB) = I_h x 30°. Le plus souvent, cet inconvénient ne sera pas gênant car les déphasages courant - tension donc les facteurs de puissance sont conservés.  

5.2 Obtention du modèle

Nous faisons les essais du transformateur avec son couplage et nous les interprétons comme si le couplage était Yy pour obtenir le schéma équivalent par phase de la fig.11.    

Pour passer des grandeurs des essais au grandeurs du modèles, nous utilisons les formules :

v     essai à vide: mesurer U₁₀, U₂₀, I₁₀, P₁₀.

v essai en court-circuit: mesurer U_1cc, I_1cc  ou I_2cc, P_1cc.

5.3 Prédéterminations

Pour effectuer les prédéterminations en charge, nous devons:

Ø      Calculer les grandeurs par phase du modèle Yy à partir des grandeurs en ligne données; pour cela nous utilisons les relations du couplage étoile: V_y = U/Ö3 et  J_y  = I.

Ø      En utilisant le schéma équivalent étoile calculer la chute de tension approchée ou avec terme correctif. En déduire la tension inconnue par la relation V_2y = m_y .V_1y - DV₂.

Ø      Revenir aux grandeurs en ligne en utilisant les relations du couplage étoile.    

6 Rendement

Le bilan des pertes est identique à celui du transformateur monophasé.

Le calcul du rendement se fait comme en monophasé en tenant compte des trois phases.

Ses propriétés sont identiques à celles énoncées en monophasé .

On pourra faire le calcul à partir du modèle équivalent :

7 couplage en parallèle

7.1 Conditions de couplage

Nous couplons en parallèle les primaires des deux transformateurs T' et T" en reliant les bornes homologues A' et A", B' et B", C' et C" pour un montage abaisseur de tension.

Pour pouvoir coupler en parallèle les bornes secondaires, les tensions secondaires doivent être égales en module et en phase pour les trois bobinages. Comme en monophasé, l'égalité des modules impose l'égalité des rapports de transformation: m' = m".

Les tensions primaires étant égales, les tensions secondaires ne pourront être en phase en couplant les bornes homologues que si les indices horaires des deux transformateurs sont identiques.

Cette deuxième condition peut être rendue moins rigoureuse en acceptant une permutation des bornes secondaires (ou primaires) d'un des transformateurs. Une permutation de bornes change l'indice horaire mais pas le groupe de couplage; pour obtenir deux indices horaires identiques en permutant les bornes d'un transformateur, il est donc nécessaire que les deux transformateurs appartiennent au même groupe de couplage.

Pour rechercher les bornes homologues à coupler, nous faisons le montage de la fig.12.

Ayant couplé les bornes a' et a", les tensions secondaires seront identiques si les deux voltmètres V et V' indiquent simultanément une tension nulle; si ce n'est pas le cas, nous essayons de permuter les bornes primaires de T" pour obtenir ce résultat. Si aucune permutation ne donne des tension nulles, T' et T" n'appartiennent pas au même groupe donc ne peuvent pas être couplés en parallèle.

7.2 Répartition de la charge

Nous remplaçons chaque transformateur par son schéma Yy équivalent; en raisonnant sur une phase de chaque transformateur équivalent, nous pouvons alors nous ramener à l'étude faite en monophasé .