Déterminer l'indice horaire et le rapport de transformation pour les transformateurs ci-dessous.
On donne n1 = 500 spires et n2 = 100 spires |
Couplage Yd
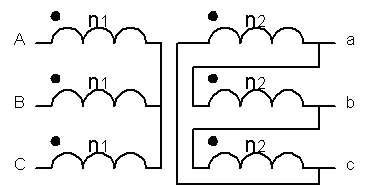
|
UAB = eB-eA ; Uab = -eb
Indice 5
m= Uab/UAB= n2./Ö3n1 = 0,115
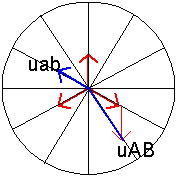
Réponse |
Couplage Zy
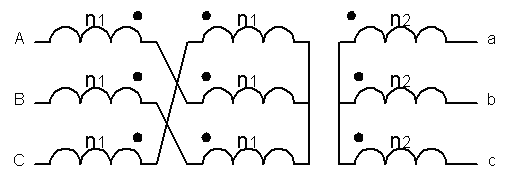
|
uAB = eA+eC-2eB =-3eB ; uab = ea-eb
Indice 1
m = Uab/UAB= Ö3.n2/3.n1 =0,115
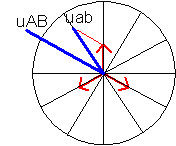
Réponse |
Dessiner un couplage possible pour un transformateur Dy3
|
| |
Si vous ne savez pas répondre directement, vous pouvez dessiner un Dy quelconque, déterminer son indice puis modifier le couplage :
* l'inversion des trois phases modifie l'indice de 6
* la permutation circulaire des phases modifie l'indice de 4
Aide |
|
Un transformateur triphasé Dy5 porte sur sa plaque signalétique :
15 kV / 400 V ; 50 Hz ; 8 kVA
L'essai à vide donne :
U1o = 15 kV ; I1o = 25 mA ; P1o = 125 W ; U2o = 410 V
L'essai en court-circuit donne :
U1cc = 655 V ; I1cc = 320 mA ; P1cc = 126 W
La résistance mesurée entre deux bornes du primaire est R'1 = 400 W |
Interprétation des données |
| Calculer le courant nominal au secondaire |
|
Calculer la résistance d'une bobine primaire
|
le primaire étant couplé en D :
R'1 = R1//2.R1 = 2.R1/3
R1 = 600 W
Réponse |
|
Déterminer les éléments du modèle d'une phase du transformateur Yy |
Pour chaque essai, calculer les grandeurs par phase en Yy : Vy=U/Ö3 ; Jy = I ; py = P/3
puis procéder comme en monophasé
Aide |
|
Fonctionnement en charge |
Le transformateur, alimenté sous U1 = 15 kV, débite I2 = 10 A sur une charge équilibrée de facteur de puissance 0,9AV. Calculer la tension secondaire, l'intensité primaire, le rendement |
Calculer les grandeurs par phase en Yy :Vy et Jy
Calculer la chute de tension en déduire V2y
Faire le bilan des puissances active et réactive; en déduire s1y, J1y et le rendement
Calculer les grandeurs en ligne U2 et I1
Aide |
|
Le transformateur alimente sous U2 = 400 V trois impédances z couplées en triangle. Chaque impédance z est modélisée par une résistance de 50 W en série avec une inductance de 120 mH.
Calculer le courant en ligne secondaire
|
Z=R+j.L.w = (62,6 W ; 37,02°)
Jch = U2/Z = 6,39 A ; Ich = I2 = Ö3.Jch = 11,1 A
Réponse |
| Calculer la tension et le courant primaire avec la charge ci-dessus |
|
| Calculer la capacité de chacun des trois condensateurs qui, couplés en étoile, permettent de ramener à 0,95 AR le facteur de puissance secondaire |
Pour 3 phases
sans C : P2 = 6140 W ; Q2 =4630VAR
avec C : P'2=P2 ; Q'2 = P'2.tgj'2 = 2018 VAR
Qc = Q'2-Q2 = -2612 VAR = -3.C.w.Vc²
Vc = 400/Ö3 ; C = 52 µF
Réponse |
| Calculer la tension et le courant primaire avec les condensateurs |
N'oubliez pas que le but du relèvement de puissance est de faire chuter l'intensité consommée
Aide |
|
On désire coupler en parallèle deux transformateurs T' et T". On donne ci-dessous leurs paramètres :
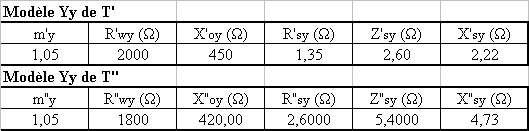
|
Couplage |
T' est de couplage Yd1 et T" de couplage Zy5 . Montrer que l'on peut coupler T' et T" en parallèle |
Les deux transformateurs ont le même rapport et appartiennent au même groupe de couplage (III)
Réponse |
Donner un schéma de couplage possible |
|
Fonctionnement en charge
Les deux transformateurs en parallèle alimentent sous U2 = 400 V une charge équilibrée consommant I2 = 10 A avec un facteur de puissance cos j2 = 0,8 AR
|
Calculer l'intensité et le facteur de puissance secondaire de chaque transformateur |
Ecrire les grandeurs en complexe en prenant v2y comme origine des phases. Dans ce cas les arguments des courants sont opposés aux déphasages correspondants
Résoudre : J2y = J'2y+J"2y ; Z'sy.J'2y = Z"sy.J"2y
Aide |
|
| Calculer la tension primaire |
Appliquer la méthode de Kapp à un des transformateurs
Aide |
|
|
Calculer le rendement de chaque transformateur et le rendement global |
|