1 Principe

Le transformateur est une machine statique à induction magnétique transformant un système de tensions périodiques en un ou plusieurs systèmes de tensions de même fréquence.

Un transformateur monophasé est composé d'au moins deux bobines couplées magnétiquement.

La bobine qui reçoit l'énergie du réseau est l'enroulement primaire et celle qui alimente la charge est l'enroulement secondaire. Pour avoir une bonne transmission de l'énergie le couplage doit être aussi serré que possible; pour cela les deux bobines sont placées sur un même circuit magnétique de forte perméabilité relative. Pour minimiser les fuites magnétiques les deux bobines sont souvent placées l'une au dessus de l'autre.

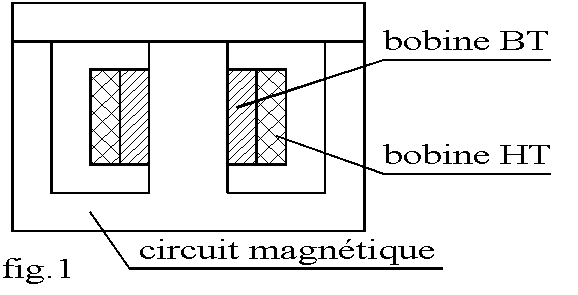
La fig.1 représente un transformateur de type cuirassé pour lequel les deux bobines sont placées sur un noyau central.

Pour les transformateurs de forte puissance, on peut utiliser un circuit magnétique rectangulaire, les bobinages étant répartis par moitié sur chaque colonne et placés l'un au-dessus de l'autre.

 

Pour des raisons d'isolement entre les enroulements et le circuit magnétique, l'enroulement soumis à la plusfaible tension ( bobine BT) est le plus proche du noyau.

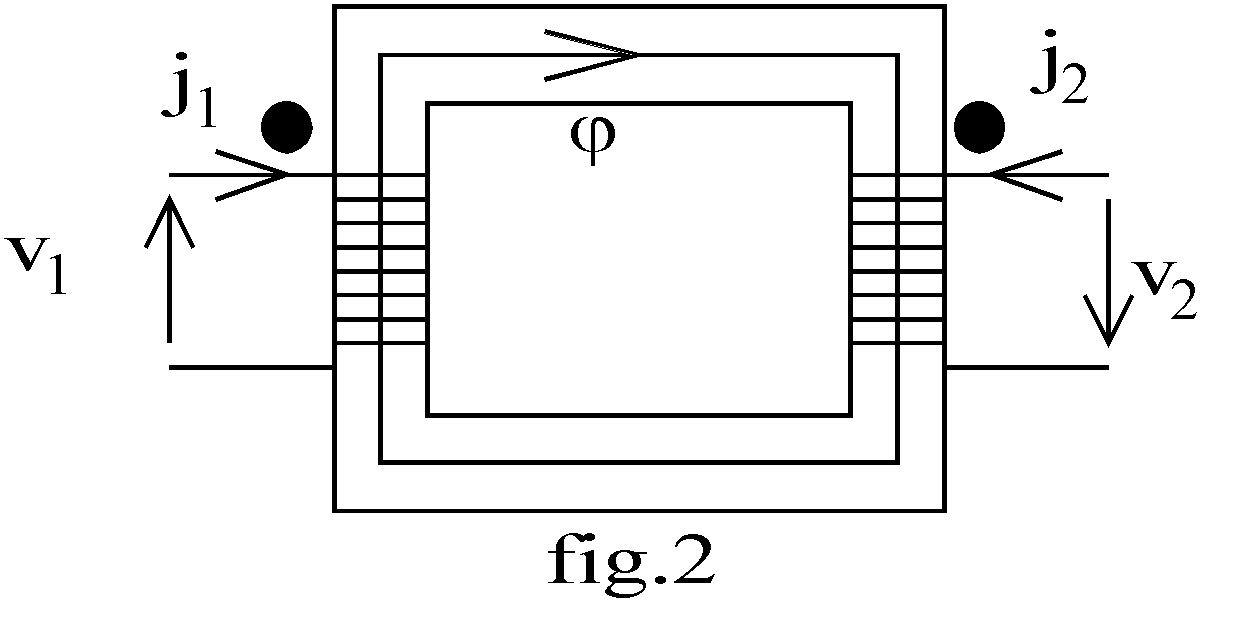
Pour avoir un schéma plus lisible, nous représentons les deux bobines séparées (fig.2). Définissons sur ce schéma les conventions de signes utilisées pour l'étude du transformateur:

è Orienter le flux j dans un sens arbitraire.

è Orienter les courants : le sens positif des courants correspond à celui qui fait circuler un flux positif. Nous utilisons la règle du tire-bouchon pour orienter les courants.

è Orienter les tensions : le primaire reçoit de l'énergie du réseau, nous utilisons donc une convention récepteur au primaire. Le secondaire fournit de l'énergie à la charge, nous utilisons donc une convention générateur au secondaire.

Lorsque nous ne représentons pas le bobinage développé mais que nous le schématisons sous forme du symbole d'une inductance, nous pouvons repérer le sens du courant donnant un flux positif en plaçant un point pour repérer la borne d'entrée de la bobine : un courant entrant par la borne repérée par le point crée des ampères-tours positifs et un courant sortant par cette borne crée des ampères-tours négatifs.

 

2 Transformateur parfait

2.1 Hypothèses

Nous dirons qu'un transformateur est parfait si:

è le circuit magnétique est parfait, c'est à dire linéaire, de réluctance nulle et sans pertes magnétiques.

è les bobinages sont parfaits: résistance nulle, fuites magnétiques nulles.

Le primaire du transformateur est alimenté par une tension sinusoïdale v1 de fréquence f. Le circuit étant linéaire, toutes les grandeurs sont sinusoïdales de fréquence f. La bobine primaire comporte n₁ spires et la bobine secondaire n₂ spires.

2.2 Équations du transformateur parfait

Soit les flux à travers la section droite du circuit, respectivement j dans le circuit magnétique, j₁ dans la bobine primaire et j₂ dans la bobine secondaire.

Les fuites étant nulles, il vient : j = j1 = j2.

La f.é.m. induite, comptée positivement dans le sens du courant, est:

v dans la bobine primaire e₁= -n₁.dj/dt

v dans la bobine secondaire e₂ = -n₂.dj/dt



Nous en déduisons e₂/e₁ = n₂/n₁ = m. Les bobines parfaites étant d'impédance interne nulle, il vient (fig.3):

v₁ = - e₁ et v₂ = e₂ . Nous avons donc v₂/v₁ = -e₂ / e₁ = -m. En valeur efficace: V₂ / V₁ = m , rapport du nombre de spires appelé rapport de transformation. Le signe - du rapport des tensions instantanées signifie qu'elles sont en opposition de phase.

Si m > 1, nous dirons que le transformateur est élévateur de tension; si m < 1, nous dirons qu'il est abaisseur de tension.

Ecrivons la loi d'Hopkinson: f.m.m. E = R.j = n₁.j₁ + n₂.j₂ . Le circuit magnétique étant parfait, sa réluctance étant nulle, il vient : j₂/j₁ = -n₁/n₂ = -1/m. Les intensités sont donc transformées dans le rapport inverse des tensions.

La puissance apparente primaire est S₁= V₁.J₁ soit S₁= (V₂/m)(m.J₂) = V₂.J₂ ; elle est donc égale à la puissance apparente secondaire S₂. Toutes les pertes étant négligées, la puissance est intégralement transmise: P₂ = P₁; le facteur de puissance cosj = P/ S est donc le même au primaire et au secondaire.

Soit B_max la valeur crête du champ magnétique dans le circuit de section droite d'aire S, nous appliquons le théorème de Boucherot ; il vient : V₁= 4,44.n₁.S.f.B_max . Pour un transformateur donné n₁ et S sont fixés, le champ B_max, donc le flux F_max, ne dépendent que de la tension efficace du réseau primaire et de sa fréquence:

Dans un transformateur parfait en régime sinusoïdal, nous dirons que le flux est forcé par la tension primaire ce qui veut dire qu'il ne dépend que de la valeur efficace et de la fréquence de cette tension.

 

Le secondaire étant à vide j₂ = 0 donc le courant primaire j₁ = -m.j₂ est nul. Le secondaire étant en charge,

j₂ ¹ 0 donc j₁ ¹ 0 ; le courant secondaire crée un flux modifiant le flux à vide; comme celui-ci doit rester constant, le primaire appelle le courant nécessaire pour annuler les ampères-tours secondaires.

2.3 Transfert d'impédance

Le secondaire étant chargé par une impédance Z_u , il vient: V₂/J₂ = Z_u. Avec les relations de transformation :

(-m.V₁) / (-J₁/m)= Z_u soit V₁/J₁ = Z_u/m^². Le réseau alimentant le primaire "voit" l'impédance Z_u/m^² dite impédance ramenée au primaire.

Inversement, une impédance Z_p placée au primaire aura le même effet que l'impédance m^².Z_p placée au secondaire.

Le transformateur a donc la propriété de modifier l'impédance vue du primaire ou du secondaire ; cette propriété donne une application du transformateur en électronique pour adapter une charge à un générateur, par exemple l'impédance faible d'un haut-parleur au dernier étage amplificateur d'un poste radio.

Lorsque l'on transfère une impédance à travers un transformateur, il faut , pour avoir équivalence, la multiplier par le carré du rapport de transformation dans le sens de transfert.

 

3 Modèle du transformateur réel

3.1 Modélisation du transformateur

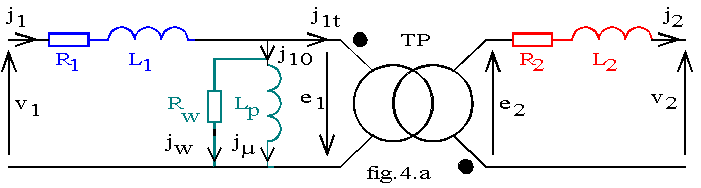
Dans le fonctionnement réel du transformateur, nous devons tenir compte de tous les défauts des bobines et du circuit magnétique. Nous utilisons les modèles définis lors de l'étude des circuits magnétiques. Il y a un seul circuit magnétique pour deux bobines donc son modèle n'apparaîtra qu'une fois dans le modèle du transformateur; l'énergie magnétisante devant être fournie même à vide, le circuit magnétique sera modélisé au primaire.

è Au primaire nous faisons apparaître (fig.4.a) :

v la résistance R₁ du bobinage

v l'inductance de fuites L₁ de la bobine primaire

v les imperfections du circuit magnétique: le courant j₁₀ est le courant sinusoïdal équivalent au courant réel à vide; R_w modélise les pertes de puissance active dans le fer et L_p la création du flux utile j dans le circuit magnétique.

è Au secondaire nous faisons apparaître les défauts de la bobine:

v la résistance du bobinage R₂

v l'inductance de fuites de la bobine L₂.

Les fuites étant modélisées, les f.é.m e₁ et e₂ sont créées par le même flux j commun aux deux bobines idéales; nous avons donc : e₁ = -n₁.dj/dt et e₂ = -n₂.dj /dt. Le couplage magnétique entre primaire et secondaire peut être modélisé par le transformateur parfait défini au paragraphe 2.

Ecrivons les équations du transformateur modélisé suivant la fig.4.a:

v au primaire: (1) V₁ = (R₁+ j.L₁.w) J₁-E₁ ; (2) E₁ = - j.n₁.w.F ;

(3) J₁ = J₁₀+J_1t = J_w + J_µ + J_1t

v transformateur parfait TP : (4) E₂ = -m.E₁ ; (5) J_1t = - m.J₂

v au secondaire: (6) V₂ = E₂ - (R₂+ j.L₂.w) J₂ ; (7) E₂ = - j.n₂.w.F

La tension efficace V₁ est différente de la f.é.m E₁; le flux j n'est plus exactement forcé par le réseau primaire; en pratique la chute de tension dans le primaire est négligeable devant V₁ donc le flux est quasi forcé. De (3) et (5) nous tirons l'équation J₁ = J₁₀ + J_1t = J₁₀ - m.J₂ d'où l'équation aux ampères-tours (8) n₁.J₁ + n₂.J₂ = n₁.J₁₀ . J_1t est le courant nécessaire pour annuler les ampères-tours secondaires; il n'apparaîtqu'en charge , nous l'appelons courant de travail.

Ce modèle équivalent permet théoriquement l'étude du transformateur; par exemple si nous fixons V₂ , J₂ et j₂ = ( j₂ ,v₂ ) nous pouvons calculer toutes les autres grandeurs si nous connaissons toutes les grandeurs du schéma équivalent. Ce modèle n'est cependant pas exploitable en pratique car il est très difficile de mesurer toutes les impédances en particulier les inductances de fuites.

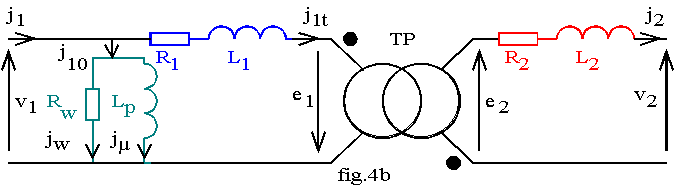
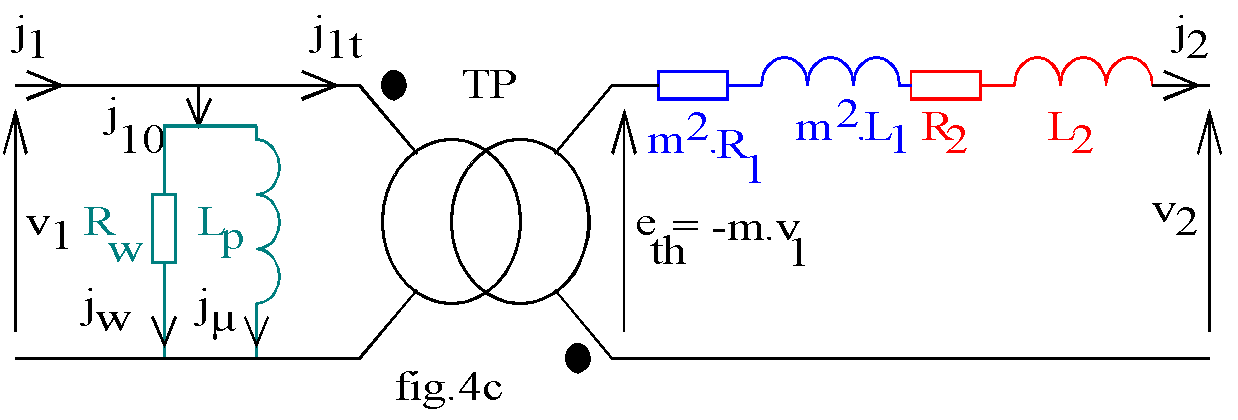
3.2 Modèle simplifié du transformateur dit "modèle de Kapp"

Lorsque le transformateur fonctionne en charge, le courant de travail est généralement grand devant le courant j₁₀; nous modifions le modèle de la fig.4.a pour obtenir celui de la fig.4.b.

La bobine représentant les imperfections du circuit magnétique a été transférée en tête du modèle.

Les différences avec le premier modèle sont :

v la chute de tension au primaire est (R₁+jL₁.w) J_1t au lieu de (R₁+jL₁.w).J₁ différence négligeable en charge.

v la bobine modélisant le circuit magnétique R_w, L_p est soumise à v₁ au lieu de e₁; le flux est forcé par la tension primaire.

Sur ce schéma, nous pouvons transférer l'impédance interne du primaire au secondaire en la multipliant par m^². Le modèle équivalent obtenu, dit de Kapp est représenté sur la fig.4.c.

Nous associons l'impédance secondaire Z₂= R₂+ j.L₂.w avec l'impédance ramenée du primaire

m^².Z₁= m^².(R₁+ j.L₁.w) pour obtenir l'impédance totale ramenée au secondaire

Z_s = Z₂ + m^².Z₁ = (R₂+ m².R₁) + j.w.(L₂+m².L₁)=R_s+j.w.L_s.

R_s et L_s sont respectivement la résistance totale et l'inductance totale de fuites ramenées au secondaire.

Les équations de ce modèle équivalent sont: (9) V₁= - E₁ ; (10) E_th = -m.E₁ ; (11) V₂ = E_th - Z_s.J₂ .

L'équation (8) aux ampères-tours n'est pas modifiée.

Vu de la charge, le transformateur est un générateur de f.é.m e_th et d'impédance interne z_s; la f.é.m e_th est égale à la tension secondaire à vide; l'impédance z_s est l'impédance vue entre les bornes de sortie lorsque lesgénérateurs de tension sont éteints, c'est à dire pour v₁ = 0 donc e_th = 0; ces éléments sont ceux du générateur de Thévenin équivalent au transformateur et au réseau primaire vus de la charge.

Ce modèle permet de réaliser simplement le bilan de puissance: soit P₂ et Q₂ les puissances active et réactive fournies par le secondaire à la charge; les pertes au secondaire sont:

è pertes actives : p_j = R_s.J₂^² = R₂.J₂^² +m².R₁.J₂^²= R₂.J₂^² +R₁.J_1t^² , valeur peu différente des pertes par effet Joule réelles R₂.J₂^² +R₁.J₁^² .

è pertes réactives q_fui =L_s.w.J₂^² ,valeur peu différente de la puissance réactive nécessaire pour magnétiser les circuits de fuites.

è Le transformateur parfait TP est sans pertes.

Au primaire les pertes dans le circuit magnétique sont:

è pertes actives p_fer =V₁^²/ R_w somme des pertes par hystérésis et par courant de Foucault.

è pertes réactives q_fer =V₁^²/ L_p.w puissance réactive magnétisante.

En appliquant le théorème de Boucherot, nous trouvons les puissances primaires:

puissance active P₁=P₂ + p_j + p_fer et puissance réactive Q₁= Q₂ + q_fui + q_fer.

3.3 Détermination expérimentale des éléments du modèle de Kapp

L'utilisation du modèle nécessite la connaissance des valeurs de R_w , L_p , m , R_s, X_s; ces éléments sont mesurés à partir de deux essais:

essai à vide

Le transformateur est alimenté sous la tension efficace V₁₀ , généralement égale à la tension nominale primaire; on mesure le courant efficace à vide J₁₀ avec un ampèremètre RMS car ce courant n'est pas sinusoïdal (ce courant à vide est de l'ordre de 5 à 10 % du courant primaire nominal), la puissance primaire P₁₀ et la tension efficace secondaire V₂₀.

Le courant secondaire étant nul, V₂₀= E_th = m.E₁ = m.V₁₀, d'où le rapport de transformation

m = V₂₀/ V₁₀.

La puissance secondaire est nulle et les pertes par effet Joule se réduisant à p_j0 =R₁.J₁₀^², la puissance

P₁₀ = P₂₀+p_j0+pfer est peu différente des pertes dans le fer. D'où la résistance R_w =V₁₀^²/P₁₀; les pertes dans le fer sont proportionnelles au carré de la tension donc R_w est indépendante de la tension d'essai.

La puissance réactive primaire peut être calculée; le facteur de puissance à vide est :

cos j₁₀ =P₁₀ /(V₁₀.J₁₀); d'où Q₁₀ =P₁₀.tg j₁₀. Cette puissance représente les pertes réactives q_fer dans le fer car la puissance réactive de fuites primaire est négligeable.

Nous en déduisons L_p.w = V₁₀^²/Q₁₀. En raison de la saturation du circuit magnétique cette réactance dépend du flux donc de la tension d'essai V₁₀. Nous la considérerons constante pour de petites variations de V₁₀ autour de sa valeur nominale.

essai en court-circuit

Nous alimentons le primaire par un alternostat et nous réglons la tension primaire V_1cc pour obtenir un courant primaire de court-circuit J_1cc voisin du courant nominal. Nous mesurons J_1cc , V_1cc , P_1cc .

Le courant secondaire peut être mesuré avec un ampèremètre mais il faut être sur que l'impédance de l'appareil est négligeable devant l'impédance interne du transformateur.

La puissance secondaire étant nulle, au primaire P_1cc = p_fercc + p_jcc .Les pertes dans le fer étant proportionnelles au carré de la tension et V_1cc n'excédant pas 10% de la tension nominale, elles sont négligeables devant les pertes par effet Joule; nous en déduisons P_1cc = p_jcc = R_s.J_2cc^². La réduction de la tension rend négligeable le courant magnétisant, d'autant plus que le circuit magnétique étant peu saturé dans cet essai, l'inductance magnétisante L_p est plus forte que sous tension nominale; donc J_2cc est peu différent

de J_1cc / m. Nous obtenons: R_s=P_1cc/ J_2cc^² = m^².P_1cc / J_1cc² .

La f.é.m efficace secondaire est E_thcc = m.E_1cc = m.V_1cc; V_2cc étant nulle, le module de l'impédance totale ramenée au secondaire est Zs =E_thcc/ J2cc soit Z_s = Ö(R_s^²+X_s^² ) = m.V_1cc /J_2cc = m^².V_1cc /J_1cc ;

nous connaissons Z_s et R_s donc la réactance de fuites X_s = L_s.w = Ö(Z_s^² - R_s^² ) .

Pour calculer la réactance de fuites, nous pouvons aussi calculer la puissance réactive Q_1cc; les pertes fer réactives sous tension réduite étant négligeables, il vient Q_1cc = X_s . J_2cc^² .

En résumé : Cliquez ici pour dérouler le scénario de modélisation

4 Fonctionnement en charge

Nous utilisons le modèle de Kapp (fig.4.c). Nous avons donc une f.é.m efficace E₁ égale à la tension d'alimentation primaire V₁; la f.é.m secondaire est E_th = m.V₁. A tension primaire constante cette f.é.m est constante; la tension secondaire V₂ = E_th - Z_s.J₂ dépend donc du courant de charge en module et phase.

A vide la tension secondaire efficace est V₂₀ = E_th = m.V₁; en charge la tension est différente de cette valeur.

La chute de tension en charge est la différence des tensions efficaces secondaires à vide et en charge pour

une même tension primaire: DV₂ = V₂₀ - V₂ = m.V₁ - V₂.

Nous ne pouvons directement exploiter (11) V₂ = E_th - Z_s J₂ pour trouver une relation sur les modules car nous ne connaissons pas la phase de E_th. Nous allons raisonner graphiquement.

4.1 Diagramme de Kapp

Donnons nous les valeurs efficaces V₂, J₂ et le déphasage j₂ =(j₂,v₂) imposé par la charge.

Traçons le diagramme de Fresnel au secondaire du modèle de Kapp; portons l'intensité secondaire suivantl'origine des phases; à l'échelle des tensions, nous traçons : OA représentant R_s.J₂ en phase avec J₂ , AB

représentant X_s.J₂ en quadrature avant sur le courant, BC représentant la tension secondaire en avance de j₂sur l'intensité. OC représente alors la f.é.m e_th ; nous en déduisons donc V₁ = E_th/m. Le cercle de centre C et de rayon CO coupe BC en H; la mesure algébrique de HB orientée dans le sens de BC représente la chute de tension DV₂ .

Dans ce diagramme le triangle OAB est appelé triangle de Kapp; l'angle (OA,OB) est égal à l'argument de l'impédance Z_s c'est à dire au déphasage primaire j_1cc en court-circuit.

4.2 Diagramme simplifié

En réalité la chute de tension est faible devant V₂; les dimensions du triangle de Kapp sont petites devant celle de OC et BC. Pour des grandeurs voisines des valeurs nominales, elles représentent quelques % de BC;il est impossible en pratique de construire, avec une bonne précision, le diagramme de la fig.5.

Projetons orthogonalement O en K' sur la droite BC. L'arc OH est de longueur faible devant le rayon du cercle; les points H et K' sont voisins et nous pouvons dire en première approximation que la chute de tension est représentée par la mesure algébrique K'B. L'angle (CO,CB) est négligeable donc les directions de OC et BC sont quasiment parallèles. Si nous projetons orthogonalement B sur OC, nous obtenons le point K; le quadrilatère OKBK' est approximativement un rectangle donc: OK est quasi égal à HB ; en première approximation, nous pouvons dire que la chute de tension en charge est représentée par la mesure algébrique OK. Avec cette hypothèse nous pouvons simplifier la construction du graphe de la fig.6, le diagramme ainsi obtenu est dit diagramme de Kapp simplifié .

Si nous voulons nous affranchir de l'imprécision graphique, nous pouvons déduire du graphe une formule donnant la chute de tension. OK représente la projection de OB sur Oy :

Cette formule approchée est valable tant que DV₂ << V₂.

4.3 Correction de la formule approchée

Lorsque J₂ augmente les dimensions du triangle de Kapp augmentent et l'approximation retenue est de moins en moins justifiée. Nous pouvons améliorer le calcul de la chute de tension en tenant compte de l'angle y.

Sur la fig.5, dans le triangle rectangle OK'C :

A la chute approchée s'ajoute un terme correctif toujours positif qui vient corriger le défaut constaté au début de ce paragraphe.

La chute de tension en charge peut être déterminée de façon approchée par la construction du diagramme de Kapp simplifié; l'expressionon de cette chute de tension est :

DV_2app= (R_s.J₂.cosj₂ + X_s.J₂.sinj₂)

Une valeur plus exacte de cette chute de tension peut-être obtenue en ajoutant à la valeur approchée ci-dessus, le terme correctif: [(R_s.sinj₂ - X_s.cosj₂).J₂]^² /(2.m.V₁).

4.4 Prédétermination du fonctionnement en charge

Problème direct

Nous nous donnons les grandeurs secondaires V₂, J₂, j₂ et nous voulons calculer la tension primaire V₁.

En utilisant le calcul simplifié nous calculons la chute de tension approchée DV_2app puis la tension primaire

V₁=( V₂ + DV_2app ) / m.

Si nous voulons une valeur plus exacte, nous devons calculer le terme correctif, mais nous ne connaissons pas la valeur de V₁ apparaissant dans ce terme. Nous pouvons dans un premier temps utiliser la valeur de V₁ approchée; si nous trouvons une valeur sensiblement différente de la valeur approchée, nous recalculons le terme correctif en utilisant la valeur corrigée de V₁ et nous recommençons par itérations successives, jusqu'à obtention d'une valeur quasi égale à celle utilisée dans le terme correctif.

Problème inverse

Nous nous donnons V₁, J₂,j₂ et nous voulons calculer V₂. Nous calculons la chute de tension approchée ou corrigée suivant la précision requise et nous en déduisons V₂ = m.V₁ - DV₂.

Dans les deux cas, le bilan de puissance (paragraphe 3.2) permet de calculer les puissances active P₁, réactive Q₁ au primaire; nous en déduisons la puissance apparente S₁ = Ö(P₁^² + Q₁^² ) , le courant primaire

J₁ = S₁ / V₁ et le facteur de puissance primaire cosj₁ = P₁ / S₁.

4.5 Caractéristiques du transformateur

Parmi les paramètres de fonctionnement V₁, J₁, j₁, V₂ , J₂, j₂ , seulement trois sont indépendants.

Nous pouvons définir les caractéristiques du transformateur:

caractéristiques externes V₂(J₂) à V₁ et j₂ constants

caractéristiques de réglage V₁(J₂) à V₂ et j₂ constants.

Les tensions primaire et secondaire étant liées, étudions la chute de tension en fonction de J₂ et j₂ en nous limitant au calcul approché. Le triangle de Kapp OAB est indépendant du déphasage, lorsque J₂ varie il se modifie homothétiquement, l'angle (OA,OB) = arg Z_s= j_cc est le déphasage mesuré en court-circuit.

 

Pour un courant donné, la chute de tension est fonction du rapport entre j₂ et j_cc; nous traçons les diagrammes de Kapp simplifiés pour diverses valeurs du déphasage et dans chaque cas pour deux courants J₂ (triangle de Kapp OAB, chute de tension OK) et J'₂ > J₂ (triangle OA'B', chute de tension OK'). Pour j₂ =0,

la chute de tension est égale à R_s.J₂; elle est donc positive et croissante en fonction du courant.

v Pour j₂ > 0 (fig.7.a) , la chute de tension est positive, croissante avec J₂. Elle croit d'abord avec j₂, est maximale pour j₂ = j_cc , puis pour j_cc < j₂ < p/2 est décroissante lorsque j₂ croît.

v Pour j₂ < 0 , la chute de tension d'abord est positive pour j_cc -p/2 < j₂ , elle s'annule, quel que soit lecourant J₂ pour j₂ = j_cc -p/2 puis devient négative (fig.7.b), c'est à dire que la tension en charge est plus grande qu'à vide .

Connaissant la variation de la chute de tension, nous pouvons donner l'allure des caractéristiques externes du transformateur (fig.8).

 

5 Pertes et rendement

5.1 Pertes du transformateur

Nous avons déjà fait le bilan de puissance du transformateur; rappelons que:

è les pertes dans le fer p_fer se décomposent en pertes par hystérésis et en pertes par courants de Foucault:

p_fer = p_h + p_cf =a.f.B_max^² + b.f^².B_max^² . Dans l'hypothèse de Kapp donc du flux forcé, B_max est proportionnel à

V₁ /f donc : p_fer = a'.V₁^² / f + b'.V₁^² ; ces pertes sont imposées par le réseau primaire et proportionnelles au carré de la tension primaire, pour une fréquence donnée: p_fer = k.V₁^².

è les pertes par effet Joule p_j = R₁.J₁^² + R₂.J₂^² ; dans l'hypothèse de Kapp, p_j = R_s.J₂^²; elles sont proportionnelles au carré de l'intensité secondaire.

5.2 Rendement du transformateur

La puissance utile est la puissance secondaire P₂ = V₂.J₂.cosj₂. La puissance absorbée est la puissanceprimaire P₁= P₂ + p_fer + p_j.

Le rendement est: h = P₂ / P₁ = V₂.J₂.cosj₂ / (V₂.J₂.cosj₂ + k..V₁^² + R_s.J₂^² ).

Le rendement croit rapidement lorsque P₂ varie de 0 à 20 ou 30% de la charge nominale; il est ensuite quasi

constant jusqu'à 110% de P_2nom puis décroît légèrement. Le rendement maximal peut dépasser 95%.

Si nous négligeons la chute de tension en charge, pour V₂ = Cste, V₁=Cste.

è Pour V₂ et J₂ constants, le rendement est fonction du facteur de puissance; les pertes étant constantes, il sera d'autant meilleur que la puissance P₂ sera grande; le rendement est maximal pour une charge résistive cos j₂=1.

è Pour V₂ et j₂ constants, le rendement est fonction de J₂:

h = V₂.J₂.cosj₂ / (V₂.J₂.cosj₂ + k.V²_² + R_s.J²_² ).)=A/(A+B/J₂+C.J₂).

Le dénominateur est seul fonction de J₂ par l'intermédiaire de deux termes, B/J₂ et C.J₂, dont le produit B.Cest constant; il sera donc minimum pour B/J₂= C.J₂ donc pour p_fer = p_j; le rendement est alors maximal.

5.3 Mesure du rendement

è La méthode directe consistant à mesurer P₁ et P₂ dans un essai en charge est peu employée; elle est imprécise et difficile à réaliser pour les transformateurs de puissance élevée.

è La méthode de pertes séparées est la plus utilisée; les pertes sont mesurées:

dans un essai à vide sous la tension V₁ donnant les pertes dans le fer

dans un essai en court-circuit sous le courant J₂ donnant les pertes par effet Joule.

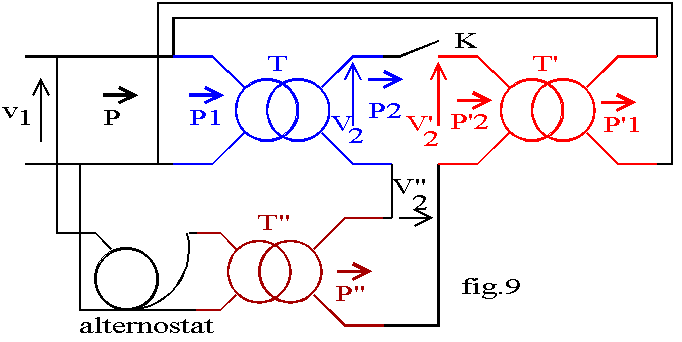
è La méthode de récupération peut être utilisée, si l'on dispose de deux transformateurs identiques.

Ces deux transformateurs T et T' sont couplés en parallèle au primaire et au secondaire; un transformateur auxiliaire T", alimenté par un alternostat, permet de charger les transformateurs (fig.9).

L'interrupteur K est ouvert à la mise sous tension; nous réglons V"₂ = 0 et nous vérifions que la tension est nulle aux bornes de K; nous avons alors couplé les bornes homologues de T et T' et nous pouvons fermer K.

Les deux transformateurs sont alimentés sous la même tension et sont parcourus par le même courant secondaire; leurs pertes sont donc identiques.

Le transformateur T reçoit au primaire la puissance P₁; il fournit au secondaire la puissance

P₂ = P₁-pertesT = P₁- p_fer -p_j.

Le transformateur T' reçoit au secondaire la puissance P'₂ = P₂+P", P" étant la puissance fournie par T". T' restitue donc au réseau P'₁=P'₂ - p_fer -p_j = P₁+ P" -2.(p_fer +p_j).

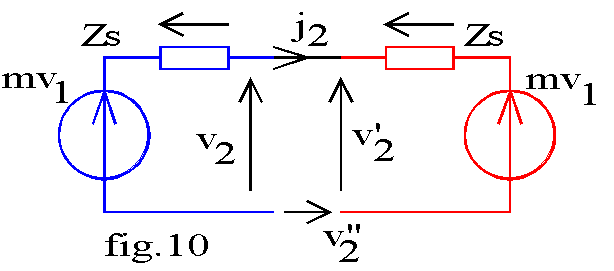
Le modèleéquivalent vu des secondaires est donné par la fig.10 :

Nous avons V₂ = m.V₁ -Z_s.J₂ , V₂ = m.V₁ + Z_s.J'₂ , V"₂ = V₂ - V'₂ = 2.Z_s.J₂ .

La puissance complexe fournie par T" est P" =V"₂.J₂*= 2.Z_s.J₂^² d'où la puissance active

P" = partie réelle(P")= P" =2.R_s. J₂^².

Il vient P" = 2.p_j et P = P₁-P'₁=2.p_fer. Le réseau ne doit fournir que les pertes de T,T',T" et de l'alternostat. En mesurant P et P" nous connaissons respectivement les pertes dans le fer et par effet Joule d'un transformateur. Ce montage a l'inconvénient d'être plus complexe que celui des pertes séparées mais a l'avantage de mesurer les pertes dans les conditions réelles de charge.

En ajoutant une impédance en série entre l'alternostat et T" ou un régulateur d'induction en cascade entre l'alternostat et T", il est possible de régler le déphasage entre v₂ et j₂, donc de réaliser l'essai en charge de T.

 

6 Couplage en parallèle de transformateurs

6.1 Principe

Nous avons vu qu'un transformateur fonctionnant avec une puissance inférieure au quart de sa valeur nominale a un rendement qui diminue rapidement. Lorsque la puissance d'une installation varie de 0 à P, il est préférable de disposer de n transformateurs de puissance nominale P/n que l'on met en service suivant la puissance appelée. La tension de la charge étant généralement imposée, les transformateurs doivent être couplés en parallèle, c'est à dire que les primaires d'une part et les secondaires d'autre part sont couplés en parallèle.

Ce mode d'alimentation permet également d'assurer une continuité de service en cas de défaillance d'un des transformateurs et facilite la maintenance.

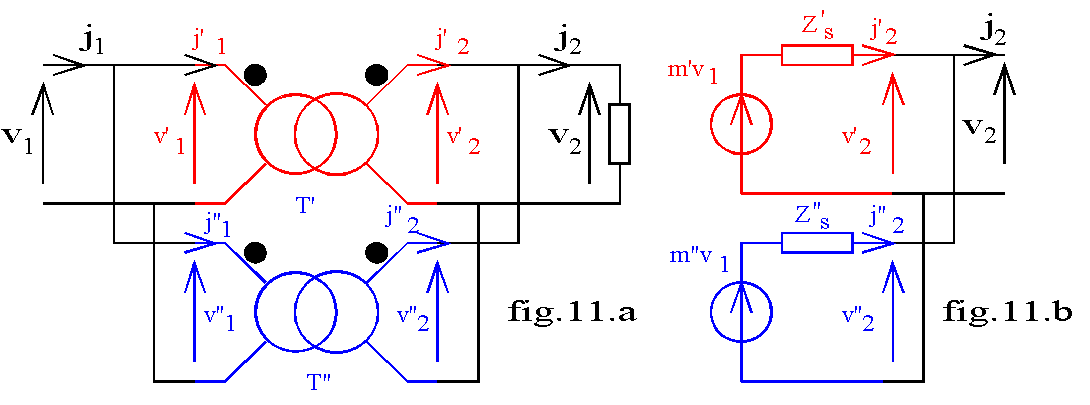
La fig.11.a représente le couplage en parallèle de deux transformateurs et la fig.11.b le schéma équivalent au montage, vu de la charge. Les primaires sont alimentés par le réseau de tension v₁= v'₁= v"₁; la charge est alimentée sous la tension v₂ = v'₂ = v"₂; elle absorbe le courant j₂ avec le facteur de puissance cosj₂.

 

6.2 Conditions de couplage

Pour éviter un court-circuit des secondaires à vide, les f.é.m secondaires doivent être égales; en valeurs efficaces on en déduit : m'.V'₁= m".V"₁; les tensions primaires étant égales, les rapports de transformation doivent être égaux. Les deux f.é.m doivent être en phase; pour cela nous devons coupler les bornes homologues repérées par les points sur fig.11.a.

Pour vérifier ces conditions, nous couplons les primaires et nous relions une borne secondaire de T' avec une de T"; nous mesurons la tension entre les deux autres bornes; cette tension doit être nulle ou négligeable devant la tension secondaire. Si c'est le cas nous pouvons relier les deux bornes secondaires; sinon il faut permuter les bornes primaires d'un des transformateurs.

6.3 Répartition de la charge

Supposons parfaitement réalisées l'égalité des f.é.m secondaires; l'égalité des tensions secondaires implique l'égalité des chutes de tensions: Z'_s.J'₂ = Z"_s.J"₂ ; les courants se répartissent proportionnellement aux impédances internes.

La loi des noeuds impose : J₂ = J'₂ + J"₂ ; des deux relations, nous déduisons:

 

7 Établissement du régime sinusoïdal permanent

Étudions un transformateur parfait alimenté par un réseau sinusoïdal. Pour t < 0, le transformateur n'est pas connecté au réseau : v₁ = v₂ = 0 ; j₁ =0; le flux forcé par la tension est nul.

A t = 0 nous alimentons le transformateur sous la tension primaire v₁= V_1m.sin(w.t-y). Le transformateur étant parfait dj/dt = v₁/n₁. En intégrant, il vient

j = - (V_1m / n₁.w ).cos(w.t - y) + A ; posons F_m = V_1m / n₁.w, valeur crête du flux en régime sinusoïdal permanent. Calculons la constante d'intégration A; à t =0 , j₁= 0 donc l'excitation magnétique h est nulle et le flux est égal au flux rémanent que nous négligeons. Il vient :

j(0) = 0 = A - F_m.cos y ; d'où j = F_m.[cosy - cos(w.t-y) ]. La valeur maximale de ce flux transitoire est F_m.[cosy +1 ] ; le cas le plus défavorable se produit lorsque nous mettons le transformateur sous tension à l'instant où la tension v₁ est nulle; nous avons alors y = 0 d'où un flux maximal égal à 2.F_m . Le flux F_m est choisi pour placer le circuit magnétique en légère saturation. Un flux double produit une très forte saturation donc un courant magnétisant très élevé. Ce courant peut dépasser le courant nominal primaire de régime permanent.

En réalité les pertes dans le fer qui augmentent comme le carré de l'induction amortissent rapidement cette pointe d'intensité à la mise sous tension.

Nous devons cependant prendre ce phénomène en compte:

v lors de l'essai à vide, il est nécessaire de court-circuiter le circuit de mesure de l'intensité

primaire à la mise sous tension; sans cela la pointe de courant peut détériorer les appareils.

v lors du choix d'un fusible au primaire , nous devons utiliser des fusibles à fusion retardée.

Notons que l'on peut éliminer le régime transitoire si y = p / 2, c'est à dire si nous mettons le transformateur sous tension lorsque la tension primaire est maximale.