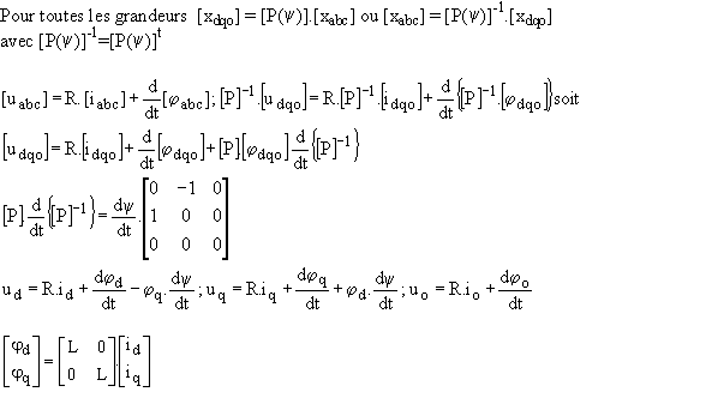F.M.M. de l'armature triphasée
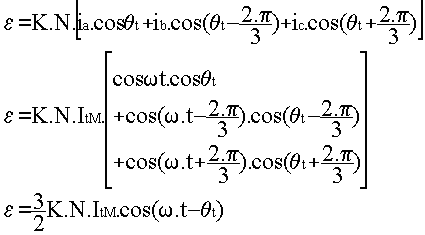
F.M.M. de l'armature triphasée
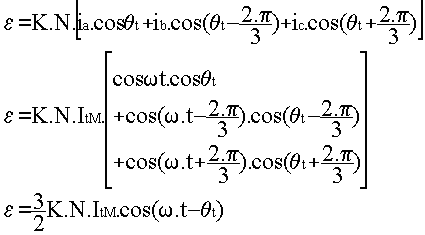
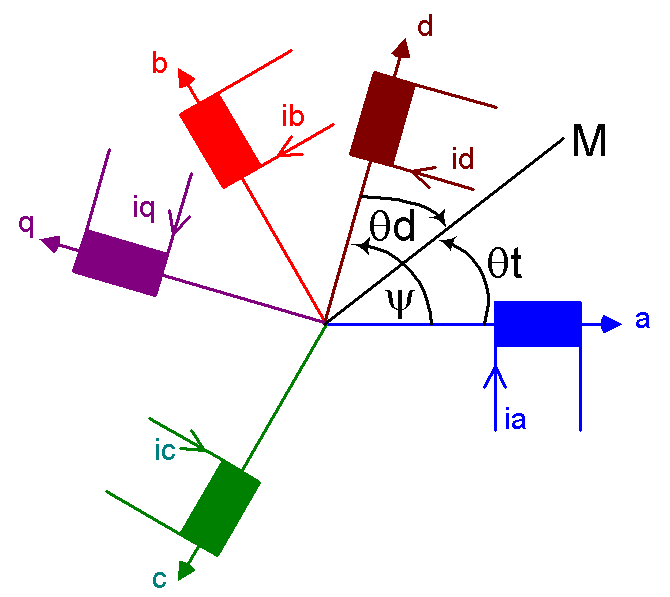
F.M.M. de l'armarure diphasée
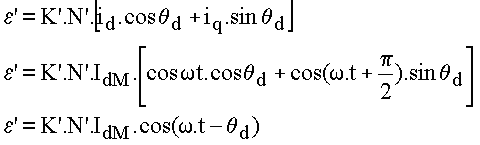
Conclusion
Les deux armatures créent un champ de même nature appelé champ tournant
On peut donc définir une équivalence
Équivalence = même f.m.m
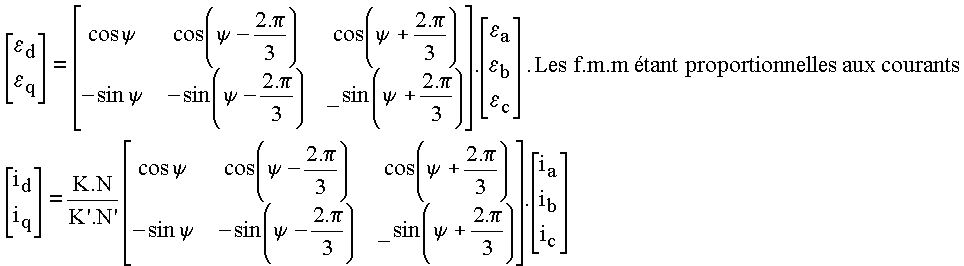
Matrice de transformation
on ajoute la composante homopolaire
xo = K.N.g.(xa + xb + xc)/K'.N'
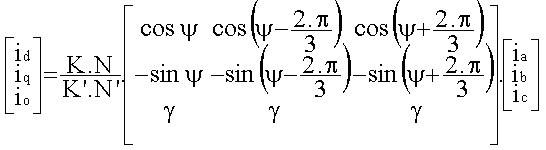
Matrice de Park
Il reste à choisir K'.N' et g
p = va.ia + vb.ib + vc.ic = vd.id + vq.iq + vo.io
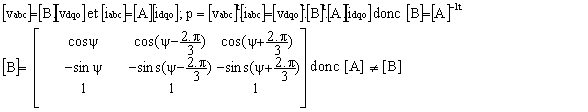
Matrice de Park :
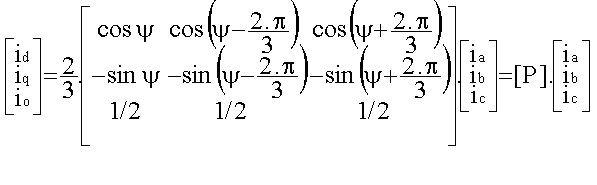
La puissance n'est pas conservée :
p = va.ia + vb.ib + vc.ic =3.( vd.id + vq.iq )/2 + 3. vo.io
Équations dans les axes d,q