Électrotechnique
Module 7 :
"Modèles avancés" xx |
Chapitre 7.1
Modèle de Park |
Les modèles électriques classiques utilisant des générateurs et des impédances ne permettent pas d'étudier de façon satisfaisante les régimes transitoires et ne sont pas adaptés à la réalisation de commandes performantes capables de maîtriser ces fonctionnements.
Il faut alors faire appel à une méthode différente de modélisation.
2.1 Description
Soit une machine monophasée au stator et au rotor :

On utilisera la représentation de la figure de droite. Chaque bobine à Kb.N spires, Kb étant le facteur de bobinage de l'armature et N son nombre de conducteurs.
On travaillera sur une machine à 2 pôles en utilisant l'angle électrique q = p.qm
¯ l'inductance propre du stator Ls
¯ l'inductance propre du rotor Lr¯ l'inductance mutuelle Lsr(q) = Msr.cosq, Msr étant la valeur de la mutuelle pour q = 0.
Expression des flux
¯ Stator : js = Ls.is + Msr.cosq.ir¯ Rotor : jr = Msr.cosq.is + Lr.ir
2.2 Etude énergétique
Les deux armatures de la machine absorbent l'énergie : 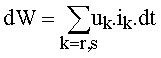
Si on décompte les pertes par effet Joule, nous obtenons la puissance utilisable :
Cette énergie sert :
¯ à créer le couple électromagnétique :
¯ à magnétiser la machine :

Nous avons en déduisons l'expression de la puissance électromagnétique : dWem = dWi - dWmagn soit :

2.3 Règle fondamentale

Le moment du couple est la somme de quatre termes sinusoïdaux de quatre fréquences différentes.
Pour que sa valeur moyenne soit différente de 0, il est nécessaire qu'au moins une des fréquences soit nulle, ce qui donne un terme constant.
La condition pour avoir un couple de moment non nul est : p.W = ±ws ± wr
¯ Pour une machine synchrone ws = 2.p.f et wr = 0. On a donc W = ±2.p.f /p , vitesse de synchronisme unique permettant d'avoir un couple moyen
¯ Pour une machine asynchrone ws = 2.p.f et wr =g.ws ; g étant le glissement :
g = (Ws –W)/Ws =(ws –p.W)/ws ; wr =(ws –p.W) .
La condition pour avoir un couple non nul est satisfaite pour toute vitesse différente du synchronisme.
3 Transformation triphasé – diphasé

L'équivalence implique que les champs magnétiques des deux armatures soient identiques .
3.1 Armature triphasée équilibrée
Une armature triphasée à 2.p pôles est formé de trois enroulements identiques dont les axes sont
décalés de 2.p/3.p et alimentées par un système équilibrés de courants triphasés.
Au point M défini par qt = (OA,OM), la forme magnétomotrice est :

L'armature triphasée crée un champ tournant
3.2 Armature diphasée équilibrée
Une armature diphasée est formée de deux bobinages d'axes orthogonaux alimentés par des courants en quadrature

Le champ créé étant de même nature que celui de l'armature triphasé, on peut établir une relation d'équivalence entre les armatures.
3.3 Transformation de Park
Si on veut que les deux armatures créent le même champ, en projetant e = ea + eb + ec sur l'axe d, on doit obtenir ed et sur l'axe q, on doit obtenir eq .
Sous forme matricielle, on a :

La matrice de transformation dite matrice de Clarke n'est pas carrée donc ne peut être inversée
pour passer du diphasé au triphasé. On va ajouter une composante dite homopolaire io = g.(ia + ib + ic )
correspondant à une f.m.m. sur un axe Oo perpendiculaire au plan (Od,Oq). Cette composante
sera généralement nulle.

Il reste à déterminer les coefficients K'.N' et g.
Plusieurs points de vue sont possible suivant les grandeurs que l'on veut conserver dans la transformation.
¯ Si on prend K.N/K’.N’ = 2/3 et g = 1/2, la transformation conserve les valeurs efficaces.
On obtient alors la matrice
¯ Si on désire conserver les puissances on doit avoir : p = va.ia + vb.ib + vc.ic = vd.id + vq.iq + vo.io ;
on adopte alors la matrice [A] pour transformer les courants et une matrice [B] pour transformer
les tensions :

Si on désire conserver les valeurs efficaces et les puissances, les matrices [A] et [B] sont différentes.
Dans la transformation de Park, on adoptera la même matrice [P] = [A] pour toutes les grandeurs tensions, courants, flux.
La puissance n’est donc pas conservée et
p = va.ia + vb.ib + vc.ic =3.( vd.id + vq.iq )/2 + 3. vo.io ;
3.4 Transformation à un axe
Dans la grande majorité des cas, le système des courants est équilibrée donc la composante homopolaire io est nulle. Le système diphasé comprend deux axes. Les grandeurs des axes d, q étant en quadrature, on peut représenter leurs valeurs par un seul nombre complexe idq = id + j.iq; on peut alors considérer que chaque armature n'a qu'un bobine parcourue par une intensité complexe.
3.5 Intérêt de la transformation
¯ Simplifier la machine en ayant moins de phases
¯ Dans une armature diphasée, les axes des bobines sont perpendiculaires donc les inductances mutuelles sont nulles entre les bobinages d, q et o.
¯ Le choix de l'angle y donne un degré de liberté permettant de simplifier les équations.
Notons que pour un système triphasé équilibré direct de pulsation w, le choix d'un axe d tournant à la vitesse angulaire w donne des grandeurs id et iq continues.
3.6 Modélisation d'une machine
Dans une machine tournante, il faudra modéliser simultanément les bobinages du stator et du rotor.
On utilise les mêmes axes d et q pour les deux armatures.

Les bobinages équivalents stator et rotor sont fixes l'un par rapport à l'autre, ce qui rend l'induction mutuelle Lsr constante.
Il y a alors deux matrices de Park correspondant à deux valeurs de y différentes : [P(qs)] pour le stator et [P(qr)] pour le rotor.
Dans une machine alternative, on peut :
v lier l'axe d au stator donc ys = 0 et yr = p.W.t
v lier l'axe d au rotor donc ys = p.W.t et yr = 0
v lier l'axe d au champ tournant stator donc ys = ws.t et yr = g.ws.t
3.7 Mise en équations d'une armature triphasée

Tensions

Flux
La matrice des flux est très simple en diphasé car la mutuelle entre les deux bobinages d'axes
perpendiculaires est nulle :

4.1 Modélisation
Le stator porte un bobinage triphasé à 2.p pôles.
Le rotor porte :
v un bobinage d'excitation alimenté par un courant continu
v un amortisseur Leblanc formé de barres placées dans les pôles du rotor et court-circuitées par des bagues sur chaque face.
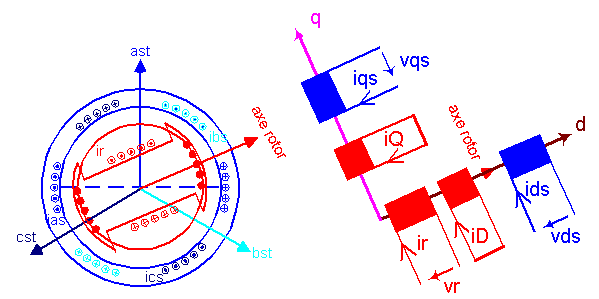
On choisit de caler l'axe d sur l'axe du rotor. On a donc ys = p.W.t et yr = 0.
v L'armature stator subit donc une transformation de Park.
v Le bobinage de magnétisation du rotor calé sur l'axe d n'est pas modifié
v L'enroulement amortisseur est décomposé en deux enroulements, l'un agissant suivant l'axe d et l'autre sur l'axe q.
4.2 Mise en équations
ys = p.W.t = ws.t et yr = 0 donc :
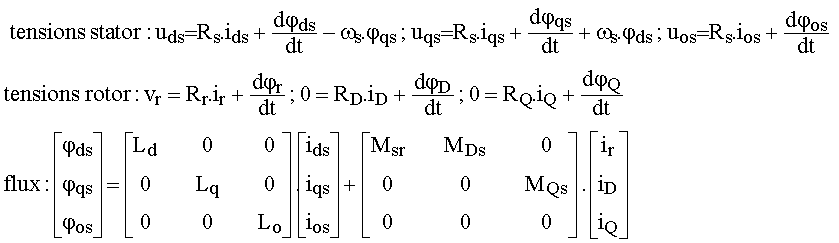
4.3 Puissance et couple
p(t) = ua.ia + ub.ib + uc.ic + vr.ir ; les enroulements amortisseurs D et Q sont en court-circuit donc ne participent pas au bilan de puissance.
p(t) = 3.(uds.ids + uqs.iqs)/2+ 3.uo.io + vr.ir = dW/dt
Avec les équations ci-dessus :
![]()
Le premier terme représente les pertes par effet Joule dans le stator et le rotor.
Le deuxième terme est de la forme i.dj = L.i.di = d(L.i²/2); il représente donc les variations d'énergie magnétique stockée dans la machine.
Le troisième terme représente donc l'énergie mécanique : dWem = Tem.dqm = Tem.ws.dt/p donc
Tem =3.p.(iqs.jds - ids.jqs)/2
Utilisons les équations

¯ Le couple synchrone Tsy est le couple de la machine synchrone. On voit qu'il est proportionnel
au flux du rotor et au courant d'axe q ; cela rappelle la machine à courant continue :
à flux constant, le couple est réglé par le courant iqs .
Si on maintient ids = 0, le flux est fixé uniquement par le courant inducteur de la machine.
¯ Le couple de réluctance Trel n'existe que dans les machines à pôles saillants : la loi du flux maximum fait que le rotor tend à aligner son pôle Nord sur le champ tournant. Pour une machine à pôles lisses Ld = Lq.
¯ Le couple asynchrone Tasy créé par la cage amortisseur n'existe que durant les phases transitoires où la vitesse du rotor est différente de la vitesse de synchronisme
5.1 Modélisation
La machine possède deux bobinages de même nature au stator et au rotor : 3 phases et 2.p pôles.
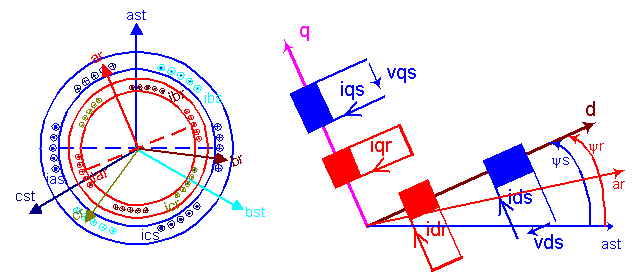
Le principe de la modélisation est d'utiliser les mêmes axes d,q pour les deux armatures. On aura donc deux matrices de Park [Ps] pour le stator avec y = ys =(ast,d) et [Pr] pour le stator avec y = yr =(ar,d).
L'avantage de ce modèle est que les inductances mutuelles entre stator et rotor sont constantes et que le flux sur un axe ne dépend que des courants stator et rotor de cet axe.
Les positions d'axe d retenues peuvent être :
Ø lier l'axe d au stator : ys = 0 et yr = w.t avec w = p.W vitesse électrique du rotor; ce choix convient pour étudier les grandeurs statoriques car [Ps] est indépendante du temps
Ø lier l'axe d au rotor : yr = 0 et ys = -w.t; ce choix convient pour étudier les grandeurs rotoriques car [Pr] est indépendante du temps
Ø lier l'axe d au champ tournant stator : ys = ws.t, avec ws = 2.p.f vitesse électrique de synchronisme;
yr = (ws-w).t = g.ws, g étant le glissement.
5.2 Mise en équations
Les équations générales du paragraphe 3.7 s'appliquent; l'absence de fil neutre au rotor et au stator
implique la nullité des composantes homopolaires. De plus les enroulements rotoriques sont en court-circuit:
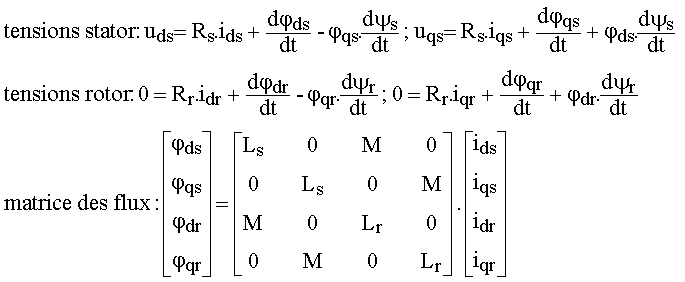
5.3 Expression du couple
Le rotor étant en court-circuit, il ne participe pas au calcul de la puissance :

5.3 Modification des équations
Les équations ci-dessus font apparaître les paramètres du rotor Rr et Lr que l’on ne peut mesurer sur une machine à rotor à cage. On doit donc modifier les équations pour obtenir un modèle utilisable dans tous les cas.
On va faire apparaître le rapport k = Ls/M, le coefficient de dispersion de Blondel caractérisant les fuites :
s = 1-M²/(Ls.Lr) et la constante de temps électrique du rotor tr = Lr/Rr.
Les grandeurs rotoriques, flux et courants sont alors multipliées par k : j’r = k.jr et i’r = k.ir.
Tous calculs faits, il vient :