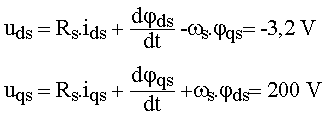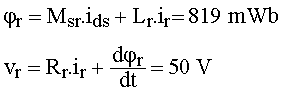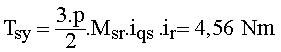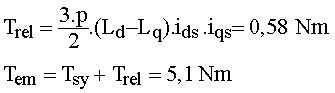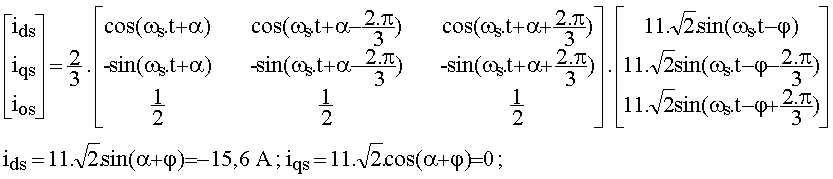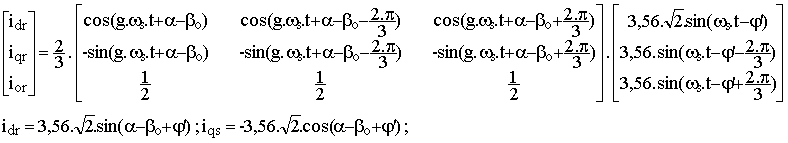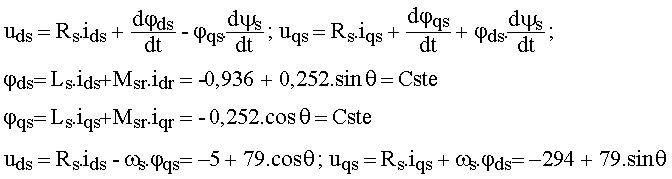Électrotechnique
Module 7 :
"Modèles avancés"
|
Chapitre 7.1
Modélisation
|
On étudie une machine synchrone triphasée à 8 pôles portant sur sa plaque signalétique : couplage Y - 2 kVA - 230 V On donne :
|
||
Le stator est alimenté par un système de tension triphasées équilibrées de fréquence f = 100 Hz; il absorbe son intensité nominale et la puissance active P = 1,6 kW ; le courant d'excitation est Ir = 5 A. |
||
1.1 Calculer la vitesse de synchronisme |
ns = 60.f / p avec p = 4 ns = 1 500 tr/min |
|
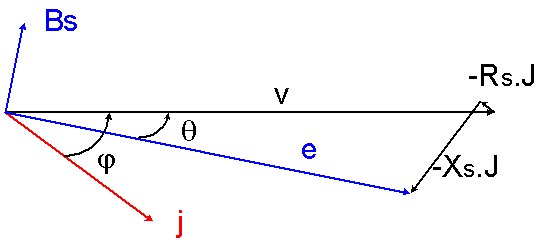
1.2 En utilisant le diagramme de Behn-Eschenburg, déterminer la f.é.m. et l'angle entre l'intensité par phase stator et le champ magnétique du rotor |
Ev = V - Rs.J-Ls.w.J
Ev = 112 V ; j = 36,87 ° ; q = 11,38 ° ; (j,Bs) = a = 90 + j - q = 115,5 ° |
|
1.2 Écrire les valeurs instantanées des courants triphasés stator en prenant l'intensité stator de la phase 1 jas comme origine des phases |
Inom = I = 2000 / Ö3 / 230 = 5 A ias = 5.Ö2.sin(w.t) ibs = 5.Ö2.sin(w.t-2.p/3) ics = 5.Ö2.sin(w.t+2.p/3) |
|
1.3 Écrire les valeurs instantanées des tensions par phase du stator |
cos j = P / S = 0,8 donc j = 0,644 rd vas = 133.Ö2.sin(w.t + j) vbs = 133.Ö2.sin(w.t + j - 2.p/3) vcs = 133.Ö2.sin(w.t+ j + 2.p/3) |
|
1.4 Si on cale l'axe d sur le champ tournant stator, quelle valeur doit-on donner à l'angle y utilisé dans la transformation de Park |
ys = p.W.t + a = 2.p.f.t + a avec a = (jas, Bs) |
|
1.5 Calculer les courants stator ids et iqs en calant l'axe d sur le champ tournant stator |
Utiliser la matrice de Park [P(ys)] avec ys = p.W.t + a = 2.p.f.t + a |
Les courants d'axe d et q sont continus |
1.6 Calculer les flux d'axes d et q du stator ; en déduire la valeur efficace du flux |
jds = Ld.ids + Msr.ir = 313,8 mWb jqs = Lq.iqs = 15,2 mWb jqs =Ö(jds²+jqs²) = 314,2 mWb |
|
1.7 Calculer les composantes d'axes d et q de la tension stator |
Utiliser les équations des axes d et q (voir cours) |
|
1.8 Calculer le flux et la tension du rotor |
|
|
1.9 Calculer le moment du couple synchrone |
|
|
1.10 Calculer le moment du couple de réluctance et celui du couple utile |
|
|
On étudie une machine asynchrone triphasée à 4 pôles; le stator et le rotor bobiné sont couplés en étoile. On donne : v pour une phase du stator ; la résistance Rs = 0,32 W ; l'inductance propre Ls = 75 mH v pour une phase du rotor ; la résistance Rr = 0,4 W ; l'inductance propre Lr = 70 mH v l'inductance mutuelle maximale stator - rotor Msr = 65 mH |
||
1 La machine alimentée par un réseau triphasé équilibré 400 V - 50 Hz tourne à la vitesse n = 1 490 tr/min.Elle absorbe les puissances active P = 2,4 kW et réactive Q = 7,25 kVAR. On néglige toutes pertes dans le fer et les pertes mécaniques. |
||
1.1 Calculer le glissement |
ns = 60.f/p = 1 500 tr /min g = (ns-n)/ns = 0,67 %
|
|
1.2 Calculer la fréquence du courant rotorique |
La fréquence du rotor est f' = g.f = 0,33 Hz |
|
1.3 Calculer l'intensité efficace dans une phase et le facteur de puissance au stator |
S = Ö(P² + Q²) = 7,64 kVA Ist = S / Ö3 / U = 11 A cos j = P / S = 0,314 AR
|
|
1.4 Calculer les puissances électromagnétique et utile |
Pem = P - pjst = pfst = P - 3.Rs.Ist² = 2,284 kW Pmot = Pem - pjr = Pem.(1-g) = 2,269 kW Pu = Pmot - pmec = Pmot = 2,269 kW
|
|
1.5 Calculer les moments du couple électromagnétique et utile |
Tem = Pem / Ws = 2 284/ (50.p) = 14,5 Nm Tu = Pu / W = 2 269/ (1 490.p /30) = 14,5 Nm
|
|
1.6 Calculer la valeur efficace du courant rotor |
pjr = g.Pem = 3.Rr.Ir² pjr = 15 W ; Ir = 3,56 A |
|
2 On utilise le modèle de Park en calant l'axe d sur le champ tournant stator |
||
2.3 Quelle valeur doit-on donner à l'angle ys de la matrice de Park du stator ? |
Se référer au théorème de Ferraris donnant le caractéristiques du champ tournant
|
Le champ tourne à la vitesse électrique de synchronisme ws=2.p.f/p et passe sur l'axe de la phase a (ys = 0) lorsque ias est maximal : ys =ws.t + a D'après 1.3 : is = 11.Ö2.sin(ws.t-j) ; is est maximal pour ws.t-j = p / 2 soit ws.t = j +p / 2 Il vient 0 = j +p / 2 + a donc a = -j -p / 2 = -162 °
|
2.4 Calculer les composantes ids et iqs des courants stator dans les axes d,q |
Le calcul est semblable à celui effectué dans l'exercice 1, question 1.5
|
|
2.5 Quelle valeur doit-on donner à l'angle yr de la matrice de Park du rotor ? |
L'axe de la phase a du rotor est décalé électriquement de b = p.W.t + bo par rapport à celle du rotor yr = ys - b = ws.t + a -p.W.t - bo ws -p.W = p.(Ws - W) = p.g. Ws yr = g.ws.t + a - bo
|
|
2.6 Exprimer les composantes idr et iqr des courants rotor dans les axes d,q en fonction du déphasage j' = (iar, vas) |
|
|
2.7 Exprimer les tensions stator uds et uqs en fonction de q = a - bo +j' |
|
|
2.8 En exprimant la conservation de la valeur efficace de la tension stator, calculer l'angle q |
V = 231 V = Ö[(uds²+uqs²)/2] 790.cosq + 46 452.sinq = -14 020 On résout par approximations successives et on obtient q = 195,4 ° |
|
2.9 Calculer les composantes idr et iqr des courants rotor |
idr = 5.sin q = -1,33 A iqs = -5.cos q = 4,82 A |
|
2.10 Calculer les composantes des flux du stator et du rotor |
jds = Ls.ids + Msr.idr = -1,26 Wb jqs = Ls.iqs + Msr.iqr = 0,313 Wb jdr = Lr.idr + Msr.ids = -1,11 Wb jqr = Lr.iqr + Msr.iqs = 0,334 Wb |
|
2.11 Calculer le moment du couple électromagnétique |
Tem = (3.p.Msr/2).(iqs.idr - ids.iqr) = 14,7 Nm |
|